3

Here's the problem.

Find the solutions of the following equation:

$$ k^2 - 1 = 5(m^2 - 1).$$

Here's my idea:

The original equation can be written as:

$$ k^2 = 5m^2 - 4 \Longleftrightarrow k^2 - 5m^2 = -4$$

I know this is Quadratic Diophantine Equation and i've done some searching on the internet and I couldn't find a particular way for solving equations of this type. Also I know that this is a varition of Pell's equation, because instead of 1 we have -4.

I actually found the fundamental solution to this equation (by guessing) and it's (1,1). Then using this algorithm (that works for Pell's equation) I tried to generate another solution and I get:

$$ X_k+_1 = aX_k + nbY_k$$ $$ X_2 = aX_1 + nbY_1$$ $$ X_2 = 1 \times 1 + 5 \times 1 \times 1 = 6$$

$$ Y_k+_1 = bX_k + aY_k$$ $$ Y_2 = bX_1 + aY_1$$ $$ Y_2 = 1 \times 1 + 1 \times 1 = 2$$

We can easily check that (6,2) isn't a solution.

So how can I transform a Quadratic Diophantine Equation into a Pell's equatuon and how can I generate more solution for Pell's equation if the constant isn't 1 (in this case it's -4)?

Bart Michels
  • 26,355
Stefan4024
  • 35,843
  • Indeed, you have $6^2 - 5 \cdot 2^2 = (-4)^2 \ne -4$, which is why that algorithm doesn't work in this case – Cocopuffs Mar 24 '13 at 23:09

3 Answers3

4

Here is the version from J. H. Conway's book, The Sensual Quadratic Form. What I do is add in the value of the quadratic form at the point in question, here in a color that is supposedly called fuchsia, then draw, as a column vector in green, the point in question. The main theorem is pages 20-23 of the book, the river is periodic. With my extra labelling, you can also see the automorph matrix $A$ at the second occurence of the form $\langle 1,0,-5 \rangle,$ as this $1$ happens at the column vector with entries $(9,4),$ then the $-5$ occurs at the column vector with entries $(20,9).$

Let's see, this is quite visual. It is probably most reasonable to say that the primitive representations of $-4$ have two representatives in each period, here given by $(1,1)$ and then $(11,5).$ In comparison, the representations of $-1$ happen only once per period, $(2,1),$ so the imprimitive representations of $-4$ come from $(4,2).$ For both primitive and imprimitive, all representations then occur using the automorph to jump from one period to the next.

Lagrange's "reduced" forms occur exactly where the value crosses the river, The value in yellow and the little arrow tell you what the equivalent form is: the reduced ones are, only, $\langle 1,4,-1 \rangle,$ and $\langle -1,4,1 \rangle.$ What this says is that the value $-4$ would not be found by continued fractions for $\sqrt 5.$

=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=

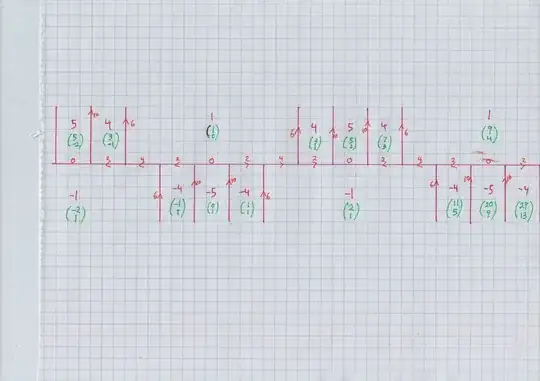
enter image description here

=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=

Will Jagy
  • 139,541
  • I actually doesn't understand this well. I think that the opposide side of the lines are $\langle α,β,γ \rangle,$ and the automorph is the green numbers so for $\langle 1,0,-5 \rangle,$ we have:

    $$ A = \left( \begin{array}{cc} 9 & 20 \ 4 & 9
    \end{array} \right) , $$

    and

    $$ A = \left( \begin{array}{cc} 1 & 0 \ 0 & 1
    \end{array} \right) , $$

     – Stefan4024 Mar 26 '13 at 11:47
  • But whta those numbers in orange color mean? you have 6 and 10 in vertical lines and 0, 2 and 4 in horizontal. How did you get them and what those mean? And one more question how did you get those numbers in green? – Stefan4024 Mar 26 '13 at 11:49
  • I've found solution to my equation and it says that for $x^2 - 5y^2 = -4$ solutions are given by: $$\frac{x_n \pm y_n\sqrt{5}}{2} = (\frac{1\pm \sqrt{5}}{2})^n \ \text{for n = 2m-1, for any m in N}$$

    How can I get generalized formula for every other quadratic Diphantine Equation.

     – Stefan4024 Mar 26 '13 at 12:07
  • @Stefan4024, I gave a link to a pdf for Conway's book. You will need to read the first chapter only. I drew this myself, then scanned it as a color jpeg, then posted to the site from my home computer. Buell's book is also very good; it is a reference here: http://en.wikipedia.org/wiki/Binary_quadratic_form and linked here http://books.google.com/books?id=qMa8-FDOR8YC&pg=PP1&lpg=PP1&dq=buell+binary+quadratic+forms&source=bl&ots=0I2rM86JSc&sig=Sl2Bud1zk_VjEO16IC4aLJZhbSI&hl=en&sa=X&ei=2edRUebMLKjziwKchoGQAw&ved=0CFwQ6AEwBA – Will Jagy Mar 26 '13 at 18:28
  • I can't understand this. Maybe it's because my lack of knowledge in English or it's maybe too complex for me, I don't know.

    I think it'll be better to show how you generate you example in the picture and explain it. Maybe it'll be clearer to me.

     – Stefan4024 Mar 26 '13 at 22:50
3

$$ A = \left( \begin{array}{cc} 9 & 20 \\ 4 & 9 \end{array} \right) , $$ and $$ A^{-1} = \left( \begin{array}{cc} 9 & -20 \\ -4 & 9 \end{array} \right). $$

$$ \left( \begin{array}{cc} 9 & 20 \\ 4 & 9 \end{array} \right) \left( \begin{array}{c} 1 \\ 1 \end{array} \right) = \left( \begin{array}{c} 29 \\ 13 \end{array} \right), $$

$$ \left( \begin{array}{cc} 9 & 20 \\ 4 & 9 \end{array} \right) \left( \begin{array}{c} 29 \\ 13 \end{array} \right) = \left( \begin{array}{c} 521 \\ 233 \end{array} \right), $$

$$ \left( \begin{array}{cc} 9 & 20 \\ 4 & 9 \end{array} \right) \left( \begin{array}{c} 521 \\ 233 \end{array} \right) = \left( \begin{array}{c} 9349 \\ 4181 \end{array} \right), $$

Switching to $-A^{-1},$ we get $$ \left( \begin{array}{cc} -9 & 20 \\ 4 & -9 \end{array} \right) \left( \begin{array}{c} 1 \\ 1 \end{array} \right) = \left( \begin{array}{c} 11 \\ -5 \end{array} \right), $$

$$ \left( \begin{array}{cc} -9 & 20 \\ 4 & -9 \end{array} \right) \left( \begin{array}{c} 11 \\ -5 \end{array} \right) = \left( \begin{array}{c} -199 \\ 89 \end{array} \right), $$

$$ \left( \begin{array}{cc} -9 & 20 \\ 4 & -9 \end{array} \right) \left( \begin{array}{c} -199 \\ 89 \end{array} \right) = \left( \begin{array}{c} 3571 \\ -1597 \end{array} \right), $$

If you want to allow common factors, $$ \left( \begin{array}{cc} 9 & 20 \\ 4 & 9 \end{array} \right) \left( \begin{array}{c} 4 \\ 2 \end{array} \right) = \left( \begin{array}{c} 76 \\ 34 \end{array} \right), $$

$$ \left( \begin{array}{cc} 9 & 20 \\ 4 & 9 \end{array} \right) \left( \begin{array}{c} 76 \\ 34 \end{array} \right) = \left( \begin{array}{c} 1364 \\ 610 \end{array} \right), $$

$$ \left( \begin{array}{cc} 9 & 20 \\ 4 & 9 \end{array} \right) \left( \begin{array}{c} 1364 \\ 610 \end{array} \right) = \left( \begin{array}{c} 24476 \\ 10946 \end{array} \right). $$

Switching to $-A^{-1},$ we get $$ \left( \begin{array}{cc} -9 & 20 \\ 4 & -9 \end{array} \right) \left( \begin{array}{c} 4 \\ 2 \end{array} \right) = \left( \begin{array}{c} 4 \\ -2 \end{array} \right), $$

$$ \left( \begin{array}{cc} -9 & 20 \\ 4 & -9 \end{array} \right) \left( \begin{array}{c} 4 \\ -2 \end{array} \right) = \left( \begin{array}{c} -76 \\ 34 \end{array} \right), $$

$$ \left( \begin{array}{cc} -9 & 20 \\ 4 & -9 \end{array} \right) \left( \begin{array}{c} -76 \\ 34 \end{array} \right) = \left( \begin{array}{c} 1364 \\ -610 \end{array} \right), $$ so you see nothing new happens this time.

Will Jagy
  • 139,541
  • How did get A ? – Stefan4024 Mar 25 '13 at 01:28
  • 2
    @Stefan4024, the discriminant of the quadratic form $x^2 - 5 y^2$ is $20,$ and the first nontrivial solution of $u^2 - 20 v^2 = 4$ is $u=18, v = 4.$ Then, given the coefficients $ \langle \alpha, \beta, \gamma \rangle = \langle 1,0,-5 \rangle$ the simplest automorph is $$ A = \left( \begin{array}{cc} \frac{u - \beta v}{2} & - \gamma v \ \alpha v & \frac{u + \beta v}{2} \end{array} \right) . $$ For larger discriminants it may not be this simple, perhaps more than one generator may be required. – Will Jagy Mar 25 '13 at 02:01
  • Good work. I'm still experiencing some problems with finding nontrivial solution to the original equation and the equation with discriminant.

    And one more question. When I write equation with discriminant, the constant (in your case 4) is negative of the constant of first equation (in this case -4). Am I right?

     – Stefan4024 Mar 25 '13 at 10:53
  • 1
    @Stefan4024 see this example about automorphs: http://math.stackexchange.com/questions/98629/non-trivial-automorph-of-an-indefinite-form and Buell's book – Will Jagy Mar 25 '13 at 19:11
2

Hint: Consider $\left(1+\sqrt{5}\right)\left(\frac{3+\sqrt{5}}{2}\right)^n$.

André Nicolas
  • 507,029
  • What does this means>? – Stefan4024 Mar 26 '13 at 12:36
  • 1
    It means that to get solutions, you expand as $a_n+b_n\sqrt{5}$, and the solutions of the Pell equation are $(a_n.b_n)$. And by using $a_{n+1}+b_{n+1}\sqrt{5}=(a_n+b_n\sqrt{5})\left(\frac{1+\sqrt{5}}{2} \right)$ you get the recurrence. – André Nicolas Mar 26 '13 at 15:15
  • I get it. For every n in N i get solution where the rational number is $a_n$ and the rational part of the irational number is $b_n$, am I right?. And why you have 1 in the comment instead of 3 in the answer in $(\frac{1+ \sqrt(5)}{2})$?

    As I understant you have to find the fundamental solution in this case (1,1). But any way to find the fundamental solution?

     – Stefan4024 Mar 26 '13 at 16:35
  • 1
    The $1$ in the comment is a typo, it is supposed to be $3$. Note that despite appearances the $a_n$, $b_n$ you get are magically integers, the $2$ at the bottom disappears. This is standard theory of the Pellian $x^2-dy^2=1$ when $d\equiv 1\pmod{4}$. You find the fundamental solution here by inspection, in general by doing a continued fraction expansion. It takes a chapter to do the full details. Nothing really hard. – André Nicolas Mar 26 '13 at 16:43
  • Thanks mate. It really helped me. I know how to do the continued fraction expansion and how to find the fundamental solution using it. But I thought maybe there are some other easier ways – Stefan4024 Mar 26 '13 at 16:51
  • There are improvements, but nothing fundamentally better. Note that in the quadratic case, the continued fraction calculation can be done using exact integer arithmetic. We certainly do not find the continued fraction by working with decimal approximations to the square root! – André Nicolas Mar 26 '13 at 16:58
  • Actually I don't know how to use it in quadratic Diophantine equation. I know that in Pell's equation I need to find the continued fraction of square root of d in $x^2 - dy^2 = 1$. But what about the quadratic Diophantine Equation. – Stefan4024 Mar 26 '13 at 18:15
  • In the positive non-square discriminant case, they can be redced to Pell equations. Negative discriminant in any particular case is simple search. – André Nicolas Mar 26 '13 at 18:22
  • I have proble with this form, with other equations. Example:

    $$x^2 - 17y^2 = 13$$

    I found the fundamental solution its $(x, y) = (9, 2)$

    So now we have:

    $$ a_n + b_n\sqrt{5} = (9 + 2\sqrt{5})(\frac{3+\sqrt{5}}{2})^n$$

    For n = 3.

    $$ a_3 + b_3\sqrt{5} = (9 + 2\sqrt{5})(\frac{3+\sqrt{5}}{2})^3$$ $$ a_3 + b_3\sqrt{5} = 121 + 54\sqrt{5}$$

    That means i have $(a_3, b_3) = (121, 54)$ as solution. But

    $$121^2 - 17x54^2 = 14641 - 49572 = - 34931$$

    Which means $(121,54)$ isn't a solution. Where am I wrong?

    And how can I reduce positive non-square discriminant case to Pell's equation?

     – Stefan4024 Mar 26 '13 at 22:43
  • Sorry, comments are not really suitable for detailled mathematics. You may want to formulate a separate question. I have not thought about your particular numerical example. In the case $x^2-dy^2=a$ there can be more than one "fundamental" solution. (For $a=\pm 1$ we always have uniqueness. Of course for $-1$ there need not be existence.) – André Nicolas Mar 26 '13 at 22:59
  • You can edit your post and explain it there better. – Stefan4024 Mar 26 '13 at 23:11