3

Prove that there are infinitely many systems of $23$ consecutive integers whose sum of squares is a perfect square.

My try: $$(n-11)^2+\cdots+(n+11)^2=23n^2+1012=23(n^2+44)=m^2$$ so $m=23k$ , $n^2=23k^2-44$. From $\mod 23$, I see $n=23l+5$ or $n=23l+18$ but i don't know what now.

Community
  • 1
Sinister
  • 585

2 Answers2

1

Dario Alpern's solver reports $n=18, k=4$ and $n=28, k=6$ as solutions, then if $(x,y)$ is a solution, so is $(24x+115y,5x+24y)$. It will show you the steps if you ask.

Ross Millikan
  • 374,822
  • There is also seed solution $n=28, k=6;$ there are two orbits giving solutions, under the automorphism group of the form. – Will Jagy Jan 05 '15 at 00:55
  • @WillJagy: The solver reported $n=18,k=-4$. I didn't notice that it generated a new list. – Ross Millikan Jan 05 '15 at 01:03
  • Anyway, by Cayley-Hamilton, we get two sequences of $n$ values under $n_{j+2} = 48 n_{j+1} - n_j,$ one is $18, 892, 42798...$ the other is $28,1362,65348...$ – Will Jagy Jan 05 '15 at 01:04
  • Ross, yes, unless the target number is $\pm 1$ we expect to get a separate list from that, and here the target is $-44.$ If the target has more prime factors that are represented by some (primitive) form of the same discriminant, we expect even more lists if there are any. – Will Jagy Jan 05 '15 at 01:07
  • Checked some things, several orbits for $x^2 - 23 y^2 = 154$ – Will Jagy Jan 05 '15 at 01:15
  • Takes a while if I do it, even with my software; anyway, four orbits for $x^2 - 23 y^2 = 154,$ seeds $(19,3);$ $(27,5);$ $(73,15);$ $(111,23).$ Alpern gets the same. – Will Jagy Jan 05 '15 at 02:11
  • @WillJagy: Where did the $154$ come from? – Ross Millikan Jan 05 '15 at 02:51
  • Not related to the original problem, I printed out small primes $p$ where either $p$ or $-p$ is represented by $x^2 - 23 y^2.$ As $2, -7, -11$ were included, I figured that their product $154$ would have more orbits. – Will Jagy Jan 05 '15 at 03:03
  • Ross, did the whole thing in Conway's pictures, posted as answer, both representing $-44$ and $154.$ Lots of work, but satisfying, and constitutes a proof that all representations (up to your $(24x+115y,5x+24y)$ mapping and its inverse) have been found. Anyway, i like it, I suppose i'm one of the few who find it worth practicing. – Will Jagy Jan 06 '15 at 19:13
1

EDIT, March 2016. Based on what people seemed to want in a recent question on Pell's equation, I wrote a program that solves $x^2 - d y^2 = k$ quite quickly, and identifies the "fundamental" solutions, from which all others can be found by applying the automorphism group.

jagy@phobeusjunior:~$ ./Pell_Target_Fundamental

  24^2 - 23 5^2 = 1

 x^2 - 23 y^2 = 154

Thu Mar 31 10:59:54 PDT 2016

x:  19  y:  3 ratio: 0.157895  fundamental 
x:  27  y:  5 ratio: 0.185185  fundamental 
x:  73  y:  15 ratio: 0.205479  fundamental 
x:  111  y:  23 ratio: 0.207207  fundamental 
x:  801  y:  167 ratio: 0.208489
x:  1223  y:  255 ratio: 0.208504
x:  3477  y:  725 ratio: 0.208513
x:  5309  y:  1107 ratio: 0.208514
x:  38429  y:  8013 ratio: 0.208514
x:  58677  y:  12235 ratio: 0.208514
x:  166823  y:  34785 ratio: 0.208514
x:  254721  y:  53113 ratio: 0.208514
x:  1843791  y:  384457 ratio: 0.208514
x:  2815273  y:  587025 ratio: 0.208514
x:  8004027  y:  1668955 ratio: 0.208514
x:  12221299  y:  2548317 ratio: 0.208514

Thu Mar 31 11:00:14 PDT 2016

 x^2 - 23 y^2 = 154

jagy@phobeusjunior:~$

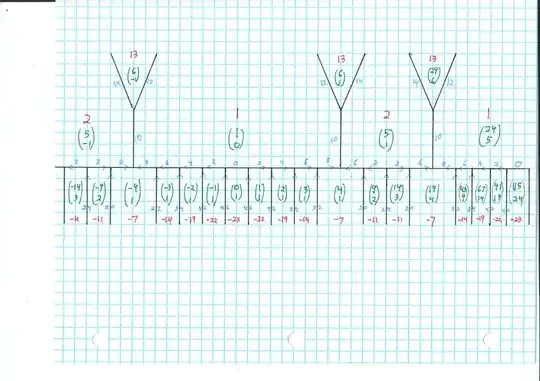
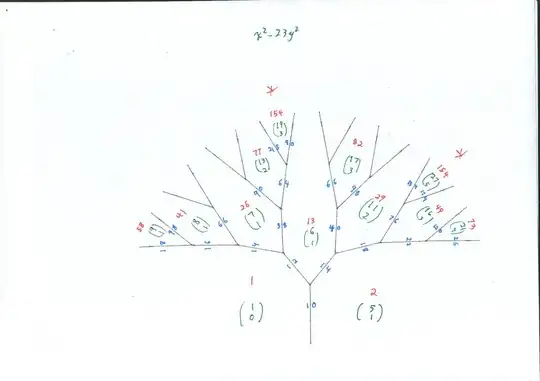
I decided to draw the complete diagram of the Conway topograph, first the river, then the two extensions (trees) away from the river that, together, give all orbits for representing $x^2 - 23 y^2 = 154,$ those four seed pairs being $$ (19,3); \; (27,5); \; (73,15); \; (111,23). $$

As far as the original posted problem, the seeds for representing $x^2 - 23 y^2 = -11$ all occur along the river. Note that, as $x^2 - 23 y^2 \equiv x^2 + y^2 \pmod 4,$ whenever $x^2 - 23 y^2 \equiv 0 \pmod 4,$ it follows that both $x,y$ are even. That is, the seeds for $-11$ are $$ (9,2); \; (14,3), $$ therefore the only seeds for $-44$ are $$ (18,4); \; (28,6). $$

You can see Ross's formula $(24x+115y, 5x+24y)$ at the far right of the river diagram, on graph paper. We see a representation of $1$ with column vector $(24,5)^T,$ below it and all the way to the edge of the paper, a representation of $-23$ with column vector $(115,24)^T.$ Put them side by side and we get the two by two matrix $$ \left( \begin{array}{cc} 24 & 115 \\ 5 & 24 \end{array} \right) $$ of determinant $+1.$ That matrix, applied to a column vector $(x,y)^T,$ gives Ross's mapping.

I used a pink pen for the represented numbers in the two tree diagrams, it is a bit hard to read; next time, always red for the represented numbers.

I put four explanatory documents at OTHER with prefix indefinite_binary. For that matter, Conway's entire book is available at PDF

enter image description here

enter image description here

enter image description here

Will Jagy
  • 139,541