Dot Product Intuition

Question

I'm searching to develop the intuition (rather than memorization) in relating the two forms of a dot product (by an angle theta between the vectors and by the components of the vector ).

For example, suppose I have vector $\mathbf{a} = (a_1,a_2)$ and vector $\mathbf{b}=(b_1,b_2)$. What's the physical or geometrical meaning that

$$a_1b_1 + a_2b_2 = |\mathbf{a}||\mathbf{b}|\cos(\theta)\;?$$

Why is multiplying $|\mathbf{b}|$ times $|\mathbf{a}|$ in direction of $\mathbf{b}$ the same as multiplying the first and second components of $\mathbf{a}$ and $\mathbf{b}$ and summing ?

I know this relationship comes out when we use the law of cosines to prove, but even then i cant get a intuition in this relationship.

This image clarifies my doubt:

Thanks

Answer 1

Start with the following definition:

(with a negative dot product when the projection is onto $-\mathbf{b}$)

This implies that the dot product of perpendicular vectors is zero and the dot product of parallel vectors is the product of their lengths.

Now take any two vectors $\mathbf{a}$ and $\mathbf{b}$.

They can be decomposed into horizontal and vertical components $\mathbf{a}=a_x\mathbf{i}+a_y\mathbf{j}$ and $\mathbf{b}=b_x\mathbf{i}+b_y\mathbf{j}$:

and so

$$\begin{align*} \mathbf{a}\cdot \mathbf{b}&=(a_x\mathbf{i}+a_y\mathbf{j})\cdot(b_x\mathbf{i}+b_y\mathbf{j}), \end{align*}$$

but the perpendicular components have a dot product of zero while the parallel components have a dot product equal to the product of their lengths.

Therefore

$$\mathbf{a}\cdot\mathbf{b}=a_xb_x+a_yb_y.$$

Answer 2

I found a reasonable proof using polar coordinates. Lets suppose the point "$a$" points is $(|a|\cos(r)$ , $|a|\sin(r) )$ and the point vector "$b$" points is ($|b|\cos(s),|b|\sin(s) $). Then doing the definition of the scalar product we get :

$a\cdot b = |a||b|\cos(r)\cos(s) + |b||a|\sin(r)\sin(s) = |a||b|\cos(r - s)$. But $\cos(r-s) = \cos(\theta)$ where theta is the angle between the vectors.

So, $a\cdot b = |a||b|\cos(\theta)$.

Answer 3

Here is the most intuitive account I could come up with. Consider the following diagram:

From the diagram we infer that $$ \begin{pmatrix}a_1\\a_2\end{pmatrix}=s\cdot\vec b+t\cdot\widehat{\vec b}=\begin{pmatrix}s b_1-t b_2\\s b_2+t b_1\end{pmatrix} $$

and therefore

$$ \begin{align} a_1 b_1+a_2 b_2&=(s b_1-t b_2)b_1+(s b_2+t b_1)b_2\\ &=s(b_1 b_1+b_2 b_2)\\ &=s|\vec b|^2\\ &=s|\vec b|\cdot|\vec b| \end{align} $$

and from the diagram it should be clear that $s|\vec b|=|\vec a|\cos\theta$ which can be substituted into the last expression above, and the result follows.

Answer 4

$\def\va{\mathbf{a}}\def\vb{\mathbf{b}}\def\vc{\mathbf{c}}$We must accept some definition of the dot product. Let us agree that the dot product between vectors $\va$ and $\vb$ is defined by $$\va\cdot\vb = |\va||\vb|\cos\theta,$$ where $\theta$ is the angle between $\va$ and $\vb$ and $0\le\theta\le\pi$. (Here we consider two-dimensional vectors, but the argument easily extends to higher dimensions.) Clearly the product is symmetric, $\va\cdot\vb=\vb\cdot\va$. Also, note that $\va\cdot\va=|\va|^2=a_x^2+a_y^2=a^2$.

There is a geometric meaning for the dot product, made clear by this definition. The vector $\va$ is projected along $\vb$ and the length of the projection and the length of $\vb$ are multiplied. If the projection is in the direction opposite that of $\vb$ the product is negative, otherwise it is positive (or zero if the projection of $\va$ is zero). This geometric picture makes obvious the claim that the dot product is distributive, $\va\cdot(\vb+\vc)=\va\cdot\vb+\va\cdot\vc.$

Consider the product $(\va+\vb)\cdot(\va+\vb).$ On the one hand, \begin{align*} (\va+\vb)\cdot(\va+\vb) &= |\va+\vb|^2 \\ &=(a_x+b_x)^2+(a_y+b_y)^2 \\ &= (a_x^2+a_y^2)+(b_x^2+b_y^2)+2(a_xb_x+a_yb_y) \\ &= a^2+b^2+2(a_xb_x+a_yb_y). \end{align*} On the other hand, using the distributive and symmetric properties of the dot product, \begin{align*} (\va+\vb)\cdot(\va+\vb) &= (\va+\vb)\cdot\va+(\va+\vb)\cdot\vb \\ &= \va\cdot\va+\vb\cdot\va+\va\cdot\vb+\vb\cdot\vb \\ &= a^2+b^2+2\va\cdot\vb. \end{align*} Therefore, $a^2+b^2+2(a_xb_x+a_yb_y) = a^2+b^2+2\va\cdot\vb$ and so $$\va\cdot\vb = |\va||\vb|\cos\theta = a_xb_x+a_yb_y.$$ Once we have shown that the dot product has the natural properties that the product is symmetric, distributive, and the dot product of a vector with itself is the magnitude of the vector squared, the relation in question follows necessarily.

Answer 5

In 2D, the claim clearly holds for $\mathbf a=(1,0)$ and $\mathbf b=(\cos \theta,\sin\theta)$, and the relation is also invariant under scaling either of the two vectors or rotating both, hence it holds for arbitrary 2D vectors.

For higher dimensions, just notice that the two vectors $\mathbf a$, $\mathbf b$ span a two-dimensional subspace, for which the argument above applies. The only difference is: In true two dimensions we could still speak of an angle in the range $[0,2\pi)$ if we wanted, but in higher dimensions this no longer makes sense as we can rotate our subspace so that the distinction between angles $<\pi$ and $>\pi$ becomes moot.

For arbitrary vector spaces with dot product, the situation is in fact upside down: One proves the Cauchy-Schwarz inequality $(\mathbf a\cdot\mathbf b)^2\le (\mathbf a\cdot\mathbf a)(\mathbf b\cdot\mathbf b)$ and concludes that there exists a unique (if both vectors are nonzero) number $c\in[-1,1]$ such that $\mathbf a\cdot\mathbf b=c\left|\mathbf a\right|\left|\mathbf b\right|$ and then defines the angle between the vectors as the unique $\theta\in[0,\pi]$ with $\cos\theta=c$.

Answer 6

I don't know if this is exactly what you are looking for, but here is an alternative geometrical or physical explanation of the identity.

Consider the vector $\underline{b}'$ which is perpendicular to $\underline{b}$ and has components $(b_2,-b_1)$

Then the area of the parallelogram formed by the vectors $\underline{a}$ and $\underline{b}'$ is, by consideration of the surrounding rectangle comprising the components, equal to $$(a_1+b_2)(a_2+b_1)-a_1a_2-b_1b_2=a_1b_1+a_2b_2$$

But the area of the parallelogram is also $$|a||b|\sin(90-\theta)=|a||b|\cos\theta$$

Answer 7

I was also uncomfortable with what is taught as standard. There is no geometric clarity like the cross product. After your question I became somewhat ruffled , but now the circle power concept developed here provides some part of the answer hopefully.

From Mechanics we know the scalar work $ F \cdot r$ is defined by dot product, but here I shall dwell on geometric aspect I record here more or less as it came to me.

The derivation of cosine of angle difference and vector dot product definition of components are in essence same, as they follow one from the other conceptually except for language/ terminology. They express cos of angle enclosed between the vectors. Same sign conventions are followed.

$$ \Delta =(a−b) $$

$$ \cosΔ=\cos a \cos b+\sin a \sin b$$

$$ \cos Δ =\frac{a_x}{\sqrt{a_x^2+a_y^2 } }\cdot\frac{b_x}{\sqrt{b_x^2+b_y^2 } } + \frac{a_y}{\sqrt{a_x^2+a_y^2 } }\cdot\frac{b_y}{\sqrt{a_x^2+a_y^2 } }$$

$$ \cos Δ =\frac{(a_x b_x + a_y b_y) }{\sqrt{a_x^2+a_y^2 } {\sqrt{b_x^2+b_y^2 }}}$$

whose numerator is nothing but the definition of a Dot product.

EDIT 1:

As for the intuition.. embarassing to admit I have none satisfactory. The way we understand parallelogram areas/cross product association, we do not understand that constant projection is also constant dot product.

The situation when two vectors have a constant cross product needs to be illustrated. If $ A = a i + 0 j $ is a fixed vector on x-axis and another vector $R = r e^{ i \theta}$ moves upwards holding center at origin.. then the two vectors have a constant dot product $I$. The tip of vector $R$ lies on a line parallel to y-axis. The projection $I//A$ is always constant.

EDIT2:

My Intuition for Vector DotProduct

Vector dot product can be seen as Power of a Circle with their Vector Difference absolute value as Circle diameter. The green segment shown is square-root of Power.

Obtuse Angle Case

Here the dot product of obtuse angle separated vectors $( OA, OB ) = - OT^2 $

EDIT 3:

A very rough sketch to scale ( 1 cm = 1 unit) for a particular case is enclosed. It convincingly shows that either projection is same, theoretically and by such verification also so that we may accept that dot product of 2 vectors is power of a circle whose vector tips are the difference vector diameter. Afik, the vector dot product had hitherto not been viewed geometrically in this way.

Answer 8

Observe that the dot product is a bilinear function:

$$(\mathbf{a'}+\mathbf{a''})\cdot(\mathbf{b'}+\mathbf{b''}) = \mathbf{a'}\cdot\mathbf{b'}+\mathbf{a''}\cdot\mathbf{b'}+\mathbf{a'}\cdot\mathbf{b''}+\mathbf{a''}\cdot\mathbf{b''}.$$

In particular, when you decompose the vectors on two orthogonal directions

$$(a_x\mathbf i+a_y \mathbf j)\cdot(b_x\mathbf i+b_y \mathbf j)$$

you get $$a_xb_x+a_yb_y.$$

because

$$\mathbf i\cdot\mathbf i=\mathbf j\cdot\mathbf j=1\cdot1\cdot\cos(0)=1, \mathbf i\cdot\mathbf j=\mathbf j\cdot\mathbf i=1\cdot1\cdot\cos\left(\frac\pi2\right)=0$$

Answer 9

Say you have a triangle with an hypotenuse of length $c$ in the plane. The hypotenuse starts at (0,0) and goes into the plane at some angle $\alpha$.

Your x-coordinate $b$, is equal to $||c||\cos(\alpha)$. Remember that $\cos(\alpha)\in[-1,1]$, so you can think about $||c||\cos(\alpha)$ as the fraction of the length of $c$ that points in the horizontal direction.

Now take the dot product $c\cdot b=(\,\,||c||\cos(\alpha)\,\,)||b||$. You are taking the part of $||c||$ that is pointing in the same direction as $||b||$ and using that for multiplying with $||b||$.

To see that this also works when $b$ isn't coinciding with the x-axis, stick a pin in the $\alpha$-corner and rotate the triangle.

I (at least) think this makes sense, two vectors have their own length and their own different directions, which means the vectors' lengths are "distributed" differently in each direction. If you want to multiply two vectors as is they were numbers, multiply the length they have in common.

So why should this equal $c_1b_1+c_2b_2$? Because of the Pythagorean theorem.

Let's say you have two vectors, $v$ and $v'$. In the case where $v=v'$, we have that $v_1v'_1+v_2v_2'=||v|| \,||v'||\cos(0)\,\,\Leftrightarrow\,\, v_1^2+v_2^2=||v||^2$, this is the familiar squares of the sides equal the square of the hypotenuse.

If you want to be a bit rude, you can think of $a_1b_1+a_2b_2=||a|| \,||b||\cos(\theta)$ as the Pythagorean theorem for when you split up the hypotenuse into different vectors, $\cos(\theta)$ then becomes a discount factor for the loss of 'shared direction' of your 'two hypotenuses'.

Answer 10

One can show that for an arbitrary rotation the scalar product remains.

Rotating so that the new x axis is around b gives: $$ a_{x'} = a\cos\theta \quad a_{y'} = a\sin\theta \quad b_{x'} = b \quad b_{y'} = 0 $$ So the scalar product is: $$ \vec{a}.\vec{b} = (a\cos\theta) \cdot b + (a\sin\theta)\cdot 0 = ab \cos\theta $$

---

proof: $$ \vec{v}.\vec{u} = v^T . u = v_x .u_x + v_y . u_y $$ Rotation Matrix: $$ R = \pmatrix{\cos\phi && -\sin\phi \\ \sin\phi && \cos\phi} $$ $$ R(\vec{v}).R(\vec{u}) = \left[\pmatrix{\cos\phi && -\sin\phi \\ \sin\phi && \cos\phi} \pmatrix{v_x \\ v_y}\right]^T . \pmatrix{\cos\phi && -\sin\phi \\ \sin\phi && \cos\phi} \pmatrix{u_x \\ u_y} $$ Evaluating: $$ \cos^2\phi u_x v_x - \cos\phi\sin\phi v_x u_y - \sin\phi \cos\phi v_y u_x + \sin^2\phi u_y v_y + \sin^2\phi u_x v_x + \sin\phi\cos\phi u_y v_x + \cos\phi \sin\phi u_x v_y + \cos^2\phi u_y v_y = v_x .u_x + v_y . u_y $$ So: $$ \vec{v}.\vec{u} = R(\vec{v}).R(\vec{u}) = v_x .u_x + v_y . u_y $$

---

So the intuition is that regardless of the rotation you choose, the scalar product remains. So you rotate to eliminate $b_y$ component.

Answer 11

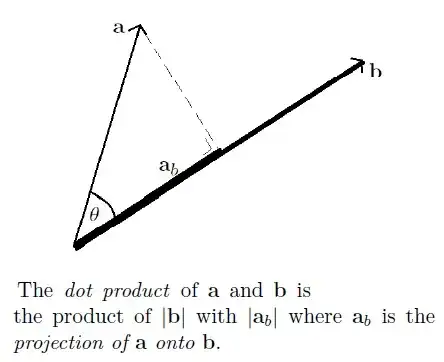
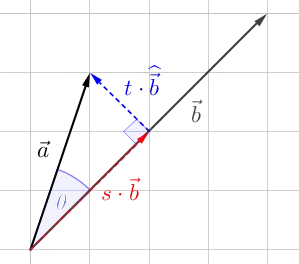
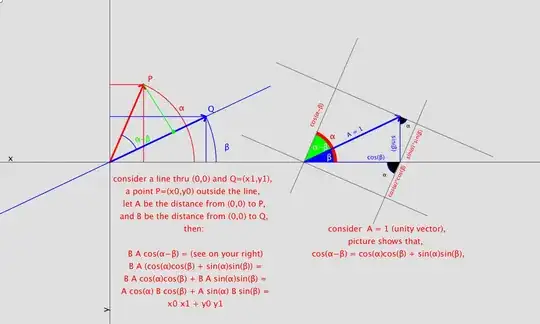
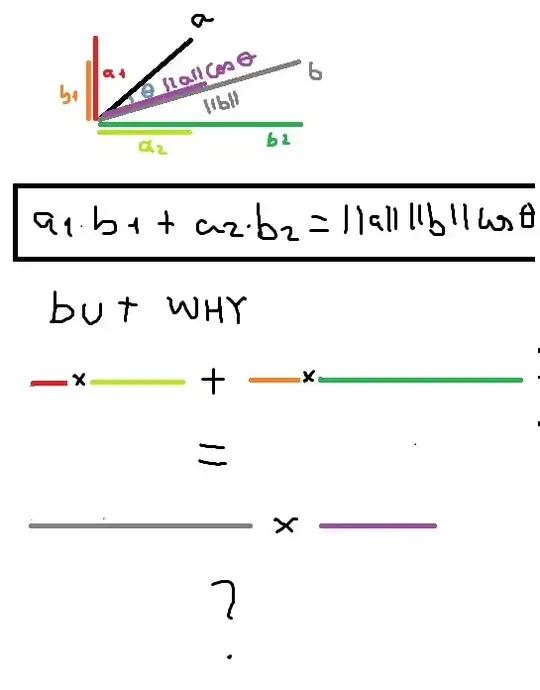Before we begin, I would like to slightly reframe the question. If we rotate a vector, its length remains the same, and if we rotate two vectors, the angle between them stays the same, so from your formula, it is easy to show that $a\cdot b = R_{\theta}(a)\cdot R_{\theta}(b)$, where $R_{\theta}(v)$ means rotating $v$ by an angle of $\theta$. I assert that this property is the conceptual geometric property that you care most about. Further, by combining this property with the fact that you can pull scalars out of the dot product, you reduce your formula to computing the dot product where $a=(1,0)$.

So how do we show $a\cdot b = R_{\theta}(a)\cdot R_{\theta}(b)$? The first step is to observe that rotation is a linear transform. Since the column vectors of the matrix of a linear transform are just where it sends the basis vectors, and it is easy to rotate the vectors $\pmatrix{1 \\ 0}$ and $\pmatrix{0 \\ 1}$, and thus to compute $$R_{\theta}=\pmatrix{\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta}.$$

Further, since $\cos (-\theta) = \cos \theta$ and $\sin (-\theta) = -\sin \theta$, we have that $R_{-\theta}=R_{\theta}^T$, the transpose. We remark that we will need to observe how matrix multiplication interacts with matrix transposition, namely $(AB)^T=B^TA^T$. Additionally, we observe that since rotating by $-\theta$ undoes rotation by $\theta$, if $M$ is the matrix for rotation by $\theta$, we have $M^TM=I$, where $I$ is the identity matrix.

Now, we are almost done. If $v$ and $w$ are vectors, written as column vectors, we can write their dot product in terms of matrix multiplication $v\cdot w = v^Tw$. Therefore, with $M$ as the matrix for rotation by $\theta$, we have $$R_{\theta}(v)\cdot R_{\theta}(w)=(Mv)\cdot (Mw)=(Mv)^T(Mw)=v^T(M^TM)w=v^TIw=v^Tw=v\cdot w.$$

Of course, this proof raises a few questions, like "Why should the transpose of a rotation matrix be the inverse?" or even more fundamental, "What does a transpose mean geometrically?" but hopefully the actual computations involved were transparent.

---

After writing my response, I was thinking about how to generalize the proof to higher dimensions. The key fact of the proof is that rotation matrices are orthogonal, which is obvious from the form of rotation matrices in two dimensions, but which is less obvious in three dimensions. We can prove it in three dimensions by showing that every rotation is a product of rotations about the coordinate axes, but this is less obvious for higher dimensions. However, there is another approach which does generalize more easily.

Polarization identity: $4(x\cdot y)=\left\|x+y \right\|^2-\left\|x-y \right\|^2$.

Proof. Using bilinearity, expand out $(x+y)\cdot (x+y)$ and $(x-y)\cdot (x-y)$.

Therefore, the dot product is completely determined by knowing the length of vectors. This gives us the following result.

Corollary: A linear map that preserves lengths also preserves dot products.

Corollary: The dot product is invariant under rotations in all dimensions.

That is the result that we wanted, arrived at simply, with no matrix multiplication, and no explicit calculations, just the observations that (1) dot products are bilinear, (2) length is defined in terms of dot products, (3) rotations are linear, and (4) rotations preserve length.

While unnecessary for our present purposes, this also fixes the hole in generalizing our original proof by giving us the following result.

Corollary: All rotation matrices are orthogonal for any reasonable definition of higher dimensional rotation.

Answer 12

The equivalence between the two definitions comes directly from the pythagorean theorem, for which the length of a vector is $$|v|=\sqrt{v_1^2+v_2^2+v_3^2},$$ where $v_i$ are the coordinates respect to some orthonormal basis (the word “some” here is important).

To see this, let $\cal V^3$ be the space of geometric vectors and $\cal B=${$e_1,e_2,e_3$}, $\cal B'$={$e'_1,e'_2,e'_3$} be two orthonormal bases of $\cal V^3$. Take $u,v\in \cal V ^3$. To show the equivalence beetween the two definitions, I'll first show that the expression $$u\cdot v=\sum u_iv_i$$ does not depend on the choice of a basis. Since the length of a vector does not depend on which set coordinates we use to evaluate it, we have:$$v _1 ^2+v _2 ^2+v _3 ^2=|v|^2=v _1' ^2+v _2' ^2+v _3' ^2,$$ where $v_i,v_i'$ are the coordinates with respect to $\cal B$ and $\cal B'$, and the same result holds for $u$. Now:$$\sum (u_i^2 +v_i^2)+\sum 2u_iv_i=\sum (u_i+v_i)^2=|u+v|^2$$

so $$\sum (u_i^2 +v_i^2)+\sum 2u_iv_i=\sum (u_i'^2 +v_i'^2)+\sum 2u_i'v_i',$$ and finally $$\sum u_iv_i=\sum u_i'v_i'.$$ So we can freely choose $\cal B$ to evaluate $u\cdot v$ and take $e_1=\frac{v}{|v|}$. This completes the proof.

---

If you are comfortable with some linear algebra, you can observe that the function that maps the coordinates $y$ of $u$ and $x$ of $v$ respect to $\cal B$ in the ones respect to $\cal B'$ is linear and given by an orthogonal matrix. So $$y^Tx=y^T (A^T A)x=(y^T A^T)(Ax)=y'^Tx'.$$

Answer 13

By the scalar product (synonymously, the dot product) of two vectors $\mathbf{A}$ and $\mathbf{B}$, denoted by $\mathbf{A} \cdot\mathbf{B}$, we mean the quantity: \begin{equation} \mathbf{A} \cdot\mathbf{B} = |\mathbf{A}| |\mathbf{B}| cos(\mathbf{A},\mathbf{B}) \end{equation} i.e., the product of the magnitudes of the vectors times the cosine of the angle between them. It follows from the above relationship that the scalar product of $\mathbf{A}$ and $\mathbf{B}$ equals the magnitude of $\mathbf{A}$ times the projection of $\mathbf{B}$ onto the direction of $\mathbf{A}$. As a matter of fact, the projection of $\mathbf{A}$ onto $\mathbf{A}$, denoted by $\mathbf{A_B}$ is length of the segment cut from $\mathbf{B}$ by the planes drawn through the end points of $\mathbf{A}$ perpendicular to $\mathbf{B}$, taken with the plus sign if the direction from the projection (onto $\mathbf{B}$) of the initial point of $\mathbf{A}$ to the projection of the end point of $\mathbf{B}$ coincides with the positive direction of $\mathbf{B}$, and with the minus sign otherwise. We can also conclude that: \begin{equation} \mathbf{A} \cdot\mathbf{B} = \mathbf{A_B} \cdot \mathbf{B} =\mathbf{A} \cdot \mathbf{B_A} \end{equation} Thus Scalar multiplication of two vectors is commutative. Given a system of rectangular coordinates ${x^1,x^2,x^3}$ let $\mathbf{i_1,i_2,i_3}$ the corresponding basis vectors. Then any vector \mathbf{A} can be represented in the form: \begin{equation} \mathbf{A} = A_1 \mathbf{i_1}+A_2 \mathbf{i_2}+A_3 \mathbf{i_3} \end{equation} Since the vectors $\mathbf{i_1,i_2,i_3}$ are orthonormal we have \begin{equation} \mathbf{i_j} \cdot \mathbf{i_k}=\delta_{j,k} \end{equation} Then \begin{equation} \mathbf{A} \cdot \mathbf{i_1} = (A_1 \mathbf{i_1}+A_2 \mathbf{i_2}+A_3 \mathbf{i_3}) \cdot \mathbf{i_1} = A_1 \end{equation} In the similar way we have $\mathbf{A} \cdot \mathbf{i_2}=A_2 $ and $\mathbf{A} \cdot \mathbf{i_3}=A_3 $. In other words, $A_1$, $A_2$ and $A_3$ are the projections of the vector $\mathbf{A}$ onto the coordinate axes. Wae can also write: \begin{equation} \mathbf{A} = (\mathbf{A} \cdot \mathbf{i_1}) \cdot \mathbf{i_1} +(\mathbf{A} \cdot \mathbf{i_2}) \cdot \mathbf{i_2} + (\mathbf{A} \cdot \mathbf{i_3}) \cdot \mathbf{i_3} \end{equation} The scalar product of two vectors A and B can easily be expressed in terms of their components: \begin{equation} \mathbf{A} \cdot \mathbf{B} = (A_1 \mathbf{i_1}+A_2 \mathbf{i_2}+A_3 \mathbf{i_3}) \cdot (B_1 \mathbf{i_1}+B_2 \mathbf{i_2}+B_3 \mathbf{i_3}) \end{equation} And when using the orthonormality condition: \begin{equation} \mathbf{A} \cdot \mathbf{B} = A_1 B_1 + A_2 B_2 +A_3 B_3 \end{equation}

Answer 14

I hope the picture shows the basic intuition underlying the definition itself of dot products.

I wished to develop the picture by Processing, by processing.org, which I consider a very interesting tool, although not so apt to develop a picture like this one.

Comments welcome

Answer 15

Let $\hat{\mathbf a}$ be the unit vector corresponding to the vector $\mathbf a$. We have that $$\mathbf a \cdot \mathbf b = ||\mathbf a || \hat{ \mathbf a }\cdot ||\mathbf b || \hat{\mathbf b} = ||\mathbf a || \ ||\mathbf b || \ \hat{\mathbf a} \cdot \hat{\mathbf b} $$

Now let $A(\mathbf a,\mathbf b) = \hat{\mathbf a} \cdot \hat{\mathbf b}$ so that $\mathbf a \cdot \mathbf b = ||\mathbf a || \ ||\mathbf b || A(\mathbf a,\mathbf b)$.

What we want to show is that $A$ is in fact the cosine of the angle between $\mathbf a$ and $\mathbf b$. Let's go with $\hat{\mathbf x},\hat{\mathbf y}$ as the usual x and y unit vectors. It's crucial here, that we use the property of the dot product, that $\hat{\mathbf x} \cdot \hat{\mathbf y} = 0$ and that $\hat{\mathbf x} \cdot \hat{\mathbf x} = \hat{\mathbf y} \cdot \hat{\mathbf y}= 1$

Now take a vector $\mathbf a = \alpha \hat{\mathbf x} + \beta \hat{\mathbf y}$. We know that $\mathbf a \cdot \hat{\mathbf x} = a$ by the above facts. We also know that $\mathbf a \cdot \hat{\mathbf x} = ||\mathbf a|| \ ||\hat{\mathbf x}|| A(\mathbf a, \hat{\mathbf x}) = ||\mathbf a|| A(\mathbf a, \hat{\mathbf x})$. If $\theta$ is the angle between $\mathbf a$ and the x-axis, then $||\mathbf a|| \cos \theta = a$.

So overall we have that $a = ||\mathbf a|| \cos \theta = \mathbf a \cdot \hat{\mathbf x} = ||\mathbf a|| A(\mathbf a, \hat{\mathbf x})$. So $\hat{\mathbf a} \cdot \hat{\mathbf x} = A(\mathbf a, \hat{\mathbf x}) = \cos \theta$ where $\theta$ is the angle between $\mathbf a$ and the x unit vector.

So from the above argument we have that $\hat{\mathbf a} \cdot \hat{\mathbf x} = \cos \theta$ where $\theta$ is the angle between $\mathbf a$ and the x unit vector. And hopefully, this is also obvious from the picture that you drew, if you take one of your vectors to lie along the x-axis. But what do we do if we take $\hat{\mathbf a} \cdot \hat{\mathbf b}$ where $\mathbf b$ may not lie along the x-axis?

You notice that we made a choice above, to choose $ \hat{\mathbf x}$ and $\hat{\mathbf y}$ as a basis to write our vectors in. So all we have to do is make another choice. Take some unit vector perpendicular to $\hat{\mathbf b}$, lets call it $\hat{\mathbf c}$. Now any vector $\mathbf a = \alpha \hat{\mathbf b} + \beta \hat{\mathbf c}$ And now repeating the above argument means that $\hat{\mathbf a} \cdot \hat{\mathbf b} = \cos \theta$ where $\cos \theta$ is the angle betwen $\mathbf a$ and $\mathbf b$.

Note that all of this, is in some sense, backwards. What the dot product is really cooked to do is to have that, in any set of orthonormal basis vectors $\{ \mathbf v_i \}_i$, that $\mathbf w = \sum_i \mathbf w \cdot \mathbf v_i \ \mathbf v_i$. It's a well defined linear function that gives us a specific formula to write vectors in terms of special sorts of basis (ones filled with perpendicular unit vectors). In this sense, we can define "the angle between two unit vectors" as the inverse cosine of the dot product between them. That is to say $\theta := \arccos(\hat{\mathbf a} \cdot \hat{\mathbf b})$. The properties of the dot product are precisely what we need for such an angle function to exist in the first place. This is the heart of why hilbert spaces and banach spaces are so different.