Here is another elegant proof in $\mathbb{R}^2$:
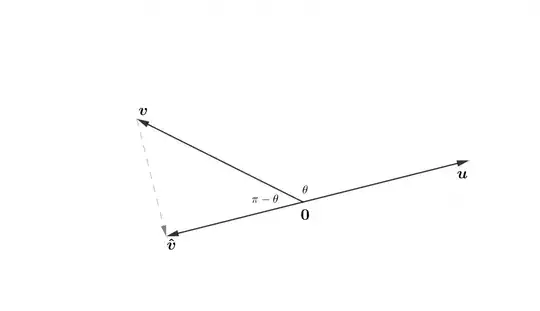
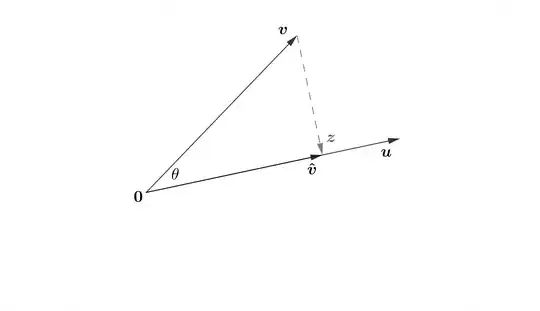
Let $\mathbf{u}$ and $\mathbf{v}$ be given. Choose $a$ such that $\hat{\mathbf{v}}=a\mathbf{u}$ forms a right triangle with $\mathbf{v}$ and $\mathbf{0}$ as shown in Figure 1. For simplicity, assume $a\gt0$ and thus $\hat{\mathbf{v}}$ makes the same angle $\theta$ with $\mathbf{v}$ (a nice exercise is to show the proof holds when $\theta$ is obtuse).
 $\tag{Fig. 1}$
$\tag{Fig. 1}$
By definition $$\tag{1}\cos\theta = \frac{|\hat{\mathbf{v}} |}{|\mathbf{v}|}.$$ Since $a\mathbf{u}=(au_1,au_2)$ and $\mathbf{z}=(z_1,z_2)$ are perpendicular their slopes multiply to $-1$: $$\frac{au_2}{au_1}\frac{z_2}{z_1}=-1\implies au_1z_1+au_2z_2=0$$ and so $$\hat{\mathbf{v}}\cdot \mathbf{z}=\hat{\mathbf{v}} \cdot (\hat{\mathbf{v}}-\mathbf{v})=0$$ $$\implies \hat{\mathbf{v}}\cdot \hat{\mathbf{v}}- \hat{\mathbf{v}}\cdot \mathbf{v}=0$$ $$\tag{2}\implies \hat{\mathbf{v}}\cdot \mathbf{v} =|\hat{\mathbf{v}}|^2. $$ Putting everything together $$a(\mathbf{u}\cdot \mathbf{v})=\hat{\mathbf{v}}\cdot \mathbf{v}=|\hat{\mathbf{v}}||\mathbf{v}|\cos\theta=a(|\mathbf{u}||\mathbf{v}|\cos\theta)$$ $$\tag{3}\implies \mathbf{u}\cdot \mathbf{v}=|\mathbf{u}||\mathbf{v}|\cos\theta. \qquad \qquad \square$$
Discussion: Going back over the proof, in particular Figure 1, we can see that the decisive step was the decomposition of the vector $\mathbf{v}$ into the sum of two vectors $$\tag{4} \mathbf{v}= \hat{\mathbf{v}} +(-\mathbf{z})=\hat{\mathbf{v}} +\mathbf{z}',$$ one a multiple of $\mathbf{u}$ and the other orthogonal to it. Alternatively, we could say that the cosine law for dot products fell out of the orthogonal projection of $\mathbf{v}$ onto the line $L$ (the $1$-dimensional subspace of $\mathbb{R}^2$ spanned by $\mathbf{u}$). In fact, the vector $\hat{\mathbf{v}}$ is called the orthogonal projection of $\mathbf{v}$ onto $\mathbf{u}$ and, as our proof shows, $$\tag{5} \hat{\mathbf{v}}=\mathbb{proj}_L\mathbf{v}=\frac{\mathbf{v}\cdot\mathbf{u}}{\mathbf{u} \cdot\mathbf{u}}\mathbf{u}.$$ Orthogonal projections naturally generalise to higher dimensions and lead to the orthogonal decomposition theorem, which states that, if $\{\mathbf{u_1},\mathbf{u_2},...,\mathbf{u_p}\}$ is any orthogonal basis of a subspace $W \subset\mathbb{R}^n$, then $$\tag{6} \hat{\mathbf{v}}=\frac{\mathbf{v}\cdot\mathbf{u_1}}{\mathbf{u_1}\cdot\mathbf{u_1}}\mathbf{u_1}+...+\frac{\mathbf{v}\cdot\mathbf{u_p}}{\mathbf{u_p}\cdot\mathbf{u_p}}\mathbf{u_p}.$$ Geometrically, this theorem states that the projection $\mathbb{proj}_W\mathbf{v}$ is the sum of $1$-dimensional projections onto the basis vectors (which coordinitise $W$). Figure 2 demonstrates the case for $\mathbb{R}^3$.
 $\tag{Fig. 2}$
$\tag{Fig. 2}$
So, with the above pictures in mind, we can outline the general proof in $\mathbb{R}^n$. Let $\mathbf{u}$ and $\mathbf{v}$ be any two linearly independent vectors in $\mathbb{R}^n$, then they span a plane $\pi$. Using the properties of orthogonal projections outlined above, the Gram-Schmidt process allows us to construct an orthonormal basis $\{\mathbf{b_1}, \mathbf{b_2}\}$ of $\pi$. Now, it easy to define (exercise) a linear transformation $T$, mapping $\{\mathbf{b_1}, \mathbf{b_2}\}$ to the standard basis $\{\mathbf{e_1}, \mathbf{e_2}\}$ of the plane $\pi'$ consisting of all n-tuples $\mathbf{x}=(x_1,x_2,0,...,0)$. The map $T$ is an isometry (exercise)-that is, $T$ is a distance preserving map: $$\tag{7} | \mathbf{u}-\mathbf{v}|= | T(\mathbf{u})-T(\mathbf{v})|.$$ Since $T$ is an isometry, it also preserves dot products. Clearly, in the plane $\pi'$, $$\tag{8} T(\mathbf{u})\cdot T(\mathbf{v})=|T(\mathbf{u})||T(\mathbf{v})|\cos\theta,$$ which we can prove by another orthogonal projection! Since $T$ is an isometry, the result must also hold in the plane $\pi$. $\qquad \qquad \square$
A Note on Isometries: A function $h:\mathbb{R}^n\rightarrow\mathbb{R}^n$ is an isometry iff it equals an orthogonal transformation followed by a translation: $$\tag{9} h(\mathbf{x})=A\mathbf{x} +\mathbf{p}.$$ There is however another, more geometrically appealing way to view isometries: as reflections. A famous result states that every isometry of $\mathbb{R}^n$ is a composition of at most $n+1$ reflections in hyperplanes. This can be visualised most evocatively in $\mathbb{R}^2$, where it is known as the three reflections theorem. A nice exercise is to show, via a drawing, that $$\tag{10} \mathbb{refl}_L \mathbf{v}=2\mathbb{proj}_L \mathbf{v}-\mathbf{v}.$$
Edit: For the case $\theta$ is obtuse, we get the following picture: