I'm looking for the intuition behind this property, hopefully one that would be at a high-school level of reasoning. Looking through several of the answers here, I came onto this one, whose answers, to me, didn't provide the intuition. (Specifically for the case of multiplying each vector's components rather than the "trig definition"). If anyone could provide a simpler, intuitive answer that would be great.
Asked
Active
Viewed 2,602 times
0
-
A lot of people like to think of the dot product as a way of measuring the "parallelness" of vectors and the cross product (when it's defined) as a way of measuring the "perpendicularness" of vectors. With this intuition, perpendicular vectors are NOT AT ALL parallel, so their dot product is zero. – Dec 01 '14 at 16:40
-
Or if you're familiar with physics, you could just always think about the concept of "work" when talking about dot products. That is, an object moving perpendicular to a force means that the force is not doing any work on that object. – Dec 01 '14 at 16:40
-
Nobody seems to have mentioned this yet: the formula $u\cdot v = |u||v| \cos \theta$ can be derived using the law of cosines, which certainly falls within most high school curricula. – Ben Grossmann Dec 01 '14 at 18:08
5 Answers
2
Let's stick to $\mathbb{R}^2$.
First notice that if one vector lies along the $x$ axis $u = x\hat{i}$ and the other $v = y\hat{j}$ lies along the $y$ axis, then their dot product is zero.
Next, take an arbitrary pair of vectors $u, v$ which are perpendicular. If we can rotate both of them so that they both lie along the axes and the dot product is invariant under that rotation, then we have the result.
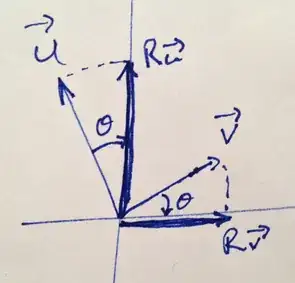
That is, let $R$ be the linear transformation or matrix such that $Ru$ and $Rv$ lie along the axes. Then if it is the case that $$Ru \cdot Rv = u \cdot v \ \ \ - (\star)$$ then we're done, because $Ru \cdot Rv = 0$ and hence $u \cdot v = 0$.
Remember that $Ru \cdot Rv = 0$ by our first observation.
That's the intuition. Make sense?
Now it turns that intuition holds up because ($\star$) is true. What follows now is some algebra demonstrating ($\star$). It takes up more room than the idea, which is unfortunate as the idea is the more important thing.
A rotation $R$ can be written for some $\theta$ as
$$R = \begin{pmatrix} \cos\theta \ \sin\theta \\ -\sin\theta \ \cos\theta \end{pmatrix}$$
Writing $u$ and $v$ now as column vectors with $u = {u_x \choose u_y}$ and $v = {v_x \choose v_y}$, then
$$Ru = \begin{pmatrix} \cos\theta \ \sin\theta \\ -\sin\theta \ \cos\theta \end{pmatrix} \begin{pmatrix} u_x \\ u_y \end{pmatrix} = \begin{pmatrix} u_x\cos\theta + u_y\sin\theta \\ -u_x\sin\theta + u_y\cos\theta \end{pmatrix}$$
Similarly,
$$Rv = \begin{pmatrix} \cos\theta \ \sin\theta \\ -\sin\theta \ \cos\theta \end{pmatrix} \begin{pmatrix} v_x \\ v_y \end{pmatrix} = \begin{pmatrix} v_x\cos\theta + v_y\sin\theta \\ -v_x\sin\theta + v_y\cos\theta \end{pmatrix}$$
Hence
$$Ru \cdot Rv = \begin{pmatrix} u_x\cos\theta + u_y\sin\theta \\ -u_x\sin\theta + u_y\cos\theta \end{pmatrix} \cdot \begin{pmatrix} v_x\cos\theta + v_y\sin\theta \\ -v_x\sin\theta + v_y\cos\theta \end{pmatrix}$$
$$ = ( u_x\cos\theta + u_y\sin\theta )(v_x\cos\theta + v_y\sin\theta) + (-u_x\sin\theta + u_y\cos\theta)(-v_x\sin\theta + v_y\cos\theta) $$
$$ = u_xv_x(\cos^2\theta + \sin^2\theta) + u_xv_y(\sin\theta\cos\theta - \sin\theta\cos\theta) + u_yv_x (\sin\theta\cos\theta - \sin\theta\cos\theta) + u_yv_y(\cos^2\theta + \sin^2\theta)$$
$$ = u_xv_x + u_yv_y$$
$$= u \cdot v$$
That is $Ru \cdot Rv = u \cdot v$, as desired.
Simon S
- 26,524
1
Using $(a_1,b_1) \cdot (a_2,b_2) = a_1a_2 + b_1b_2$, having a dot product of zero means $$ \frac{b_1}{a_1} = - \frac{a_2}{b_2}, $$ so the "slope" of one vector is negative the reciprocal of the "slope" of the other, which means they are perpendicular.
Santiago Canez
- 2,511
1
Consider two vectors $A$ and $B$. By projecting on $A$, decompose $B$ in a parallel and a normal component.
As regards the modules (lengths),
the dot product is the product of $A$ and $B^\parallel$,
the cross product is the product of $A$ and $B^\perp$.
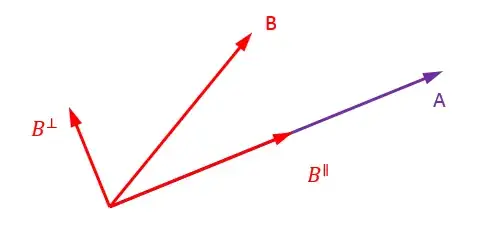
What can you conclude when $B^\parallel=0$ or $B^\perp=0$ ?
0
For your specific question of why the dot product is 0 for perpendicular vectors, think of the dot product as the magnitude of one of the vectors times the magnitude of the part of the other vector that points in the same direction. So, the closer the two vectors' directions are, the bigger the dot product. When they are perpendicular, none of vector A is going in the direction of vector B.
In the image below, dot product is |B||A|cos$\theta$.
|A|cos$\theta$ can be thought of as the amount of A going in the direction of B.
turkeyhundt
- 7,733
-
OK so that would work for the dot product equaling |a||b|cos(θ), but what about when you're multiplying the components of vectors (a1b1+a2b2)? – idanp Dec 01 '14 at 16:50
-
If they are perpendicular, they will share no common components. Imagine they are on the x and y axes, respectively. One vector is all x and the other is all y. So the x component of A times the x component of B will be zero (since B consists only of y direction). Similarly multiplying the y components will give zero also. Then, to generalize, rotating this pair of vectors together will not change their dot product. – turkeyhundt Dec 01 '14 at 16:54
0
It can be though as the component of one vector along the other, since they are perpendicular they have no mutual componenets, or in another sense they are very dissimiliar, belonging to entirely different dimensions, for vectors that are very similiar and are close dimensionally, the dot product is large.
In the image below, dot product is |B||A|cos$\theta$.
|A|cos$\theta$ can be thought of as the amount of A going in the direction of B.
turkeyhundt
- 7,733
RE60K
- 17,716