Why is the SVM margin equal to $\frac{2}{\|\mathbf{w}\|}$?

Question

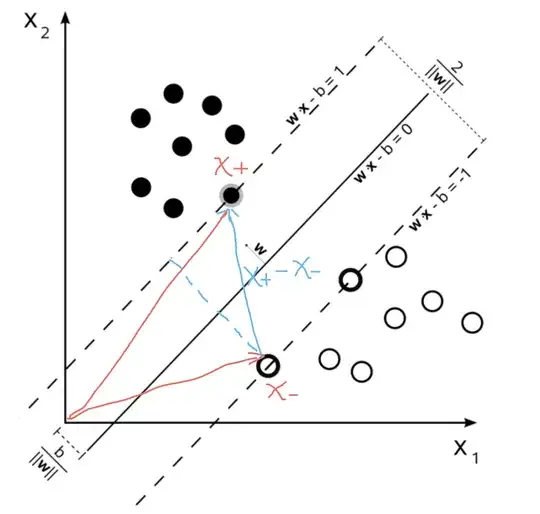
I am reading the Wikipedia article about Support Vector Machine and I don't understand how they compute the distance between two hyperplanes.

In the article,

By using geometry, we find the distance between these two hyperplanes is $\frac{2}{\|\mathbf{w}\|}$

I don't understand how the find that result.

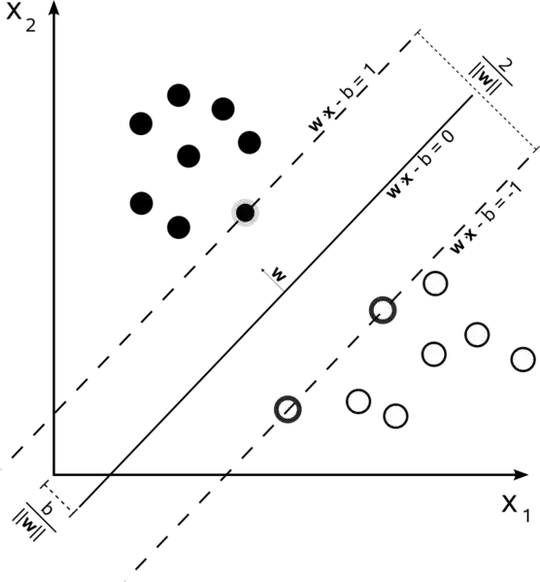
What I tried

I tried setting up an example in two dimensions with an hyperplane having the equation $y = -2x+5$ and separating some points $A(2,0)$, $B(3,0)$ and $C(0,4)$, $D(0,6)$ .

If I take a vector $\mathbf{w}(-2,-1)$ normal to that hyperplane and compute the margin with $\frac{2}{\|\mathbf{w}\|}$ I get $\frac{2}{\sqrt{5}}$ when in my example the margin is equal to 2 (distance between $C$ and $D$).

How did they come up with $\frac{2}{\|\mathbf{w}\|}$ ?

Answer 1

Let $\textbf{x}_0$ be a point in the hyperplane $\textbf{wx} - b = -1$, i.e., $\textbf{wx}_0 - b = -1$. To measure the distance between hyperplanes $\textbf{wx}-b=-1$ and $\textbf{wx}-b=1$, we only need to compute the perpendicular distance from $\textbf{x}_0$ to plane $\textbf{wx}-b=1$, denoted as $r$.

Note that $\frac{\textbf{w}}{\|\textbf{w}\|}$ is a unit normal vector of the hyperplane $\textbf{wx}-b=1$. We have $$ \textbf{w}(\textbf{x}_0 + r\frac{\textbf{w}}{\|\textbf{w}\|}) - b = 1 $$ since $\textbf{x}_0 + r\frac{\textbf{w}}{\|\textbf{w}\|}$ should be a point in hyperplane $\textbf{wx}-b = 1$ according to our definition of $r$.

Expanding this equation, we have \begin{align*} & \textbf{wx}_0 + r\frac{\textbf{w}\textbf{w}}{\|\textbf{w}\|} - b = 1 \\ \implies &\textbf{wx}_0 + r\frac{\|\textbf{w}\|^2}{\|\textbf{w}\|} - b = 1 \\ \implies &\textbf{wx}_0 + r\|\textbf{w}\| - b = 1 \\ \implies &\textbf{wx}_0 - b = 1 - r\|\textbf{w}\| \\ \implies &-1 = 1 - r\|\textbf{w}\|\\ \implies & r = \frac{2}{\|\textbf{w}\|} \end{align*}

Answer 2

Let $\textbf{x}_+$ be a positive example on one gutter, such that $$\textbf{w} \cdot \textbf{x}_+ - b = 1$$

Let $\textbf{x}_-$ be a negative example on another gutter, such that $$\textbf{w} \cdot \textbf{x}_- - b = -1$$

The width of margin is the scalar projection of $\textbf{x}_+ - \textbf{x}_-$ on unit normal vector , that is the dot production of $\textbf{x}_+ - \textbf{x}_-$ and $\frac{\textbf{w}}{\|\textbf{w}\|}$

\begin{align} width & = (\textbf{x}_+ - \textbf{x}_-) \cdot \frac{\textbf{w}}{\|\textbf{w}\|} \\ & = \frac {(\textbf{x}_+ - \textbf{x}_-) \cdot {\textbf{w}}}{\|\textbf{w}\|} \\ & = \frac{\textbf{x}_+ \cdot \textbf{w} \,{\bf -}\, \textbf{x}_-\cdot \textbf{w}}{\|\textbf{w}\|} \\ & = \frac{1-b-(-1-b)}{\lVert \textbf{w} \rVert} \\ & = \frac{2}{\|\textbf{w}\|} \end{align}

The above refers to MIT 6.034 Artificial Intelligence

Answer 3

The margin equals the shortest distance between the points of the two hyperplanes. Let $\mathbf{x_1}$ be a point of one hyperplane, and $\mathbf{x}_2$ be a point of the other hyperplane. We want to find the minimal value of $\lVert \mathbf{x}_1 - \mathbf{x}_2 \rVert$. Since \begin{align} \mathbf{w}\cdot\mathbf{x}_1 - b &= 1,\\ \mathbf{w}\cdot\mathbf{x}_2 - b &= -1, \end{align} we have $$\mathbf{w}\cdot(\mathbf{x}_1 - \mathbf{x}_2) = 2.$$ By the Cauchy-Schwarz inequality, we have $$\lVert \mathbf{w} \rVert \lVert \mathbf{x}_1 - \mathbf{x}_2 \rVert \geq 2,$$ and therefore $$\lVert \mathbf{x}_1 - \mathbf{x}_2 \rVert \geq \frac{2}{\lVert \mathbf{w} \rVert },$$ where equality holds when $\mathbf{w}$ and $\mathbf{x}_1-\mathbf{x}_2$ are linearly dependent (which is clearly always possible).