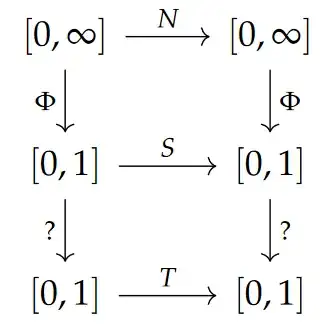Produce an explicit bijection between rationals and naturals

Question

I remember my professor in college challenging me with this question, which I failed to answer satisfactorily: I know there exists a bijection between the rational numbers and the natural numbers, but can anyone produce an explicit formula for such a bijection?

Answer 1

We will first find a bijection $h_{+}:\mathbb Z^+\to \mathbb Q^+$. From there, we easily get a bijection $h:\mathbb Z\to \mathbb Q$ by defining: $$h(n)=\begin{cases}h_{+}(n)&n>0\\ 0&n=0\\ -h_{+}(-n)&n<0 \end{cases}$$

From there, we can use any of the bijections $\mathbb N\to\mathbb Z$ to get our bijection between $\mathbb N$ and $\mathbb Q$. (We'll need a specific such bijection below, $s$.)

Now, every positive integer can be written uniquely as $p_1^{a_1}p_2^{a_2}\cdots$, where the $p_1=2,p_2=3,p_3=5,\dots$ is the sequence of all primes, and the $a_i$ are non-negative integers, and are non-zero for only finitely many $i$s.

Similarly, every positive rational number can be written uniquely as $p_1^{b_1}p_2^{b_2}\cdots$ where the $b_i$ are integers and only finitely many of the $b_i$ are non-zero.

So define $s:\mathbb N\to\mathbb Z$ (where we take $\mathbb N$ to include $0$):

$$s(n)= (-1)^n\left\lfloor\frac{n+1}{2}\right\rfloor $$

The sequence $s(0),s(1),s(2),s(3),\dots$ would be $0,-1,1,-2,2\dots$, and this is a bijection from $\mathbb N$ to $\mathbb Z$. The only properties we really need for $s$ is that $s$ is a bijection and $s(0)=0$.

Then for any $n=p_1^{a_1}p_2^{a_2}\cdots\in\mathbb Z^+$, define $$h_{+}(n)=p_1^{s(a_1)}p_2^{s(a_2)}\cdots $$

This then defines our bijection $h_{+}:\mathbb Z^+\to \mathbb Q^{+}$.

A potientially interesting feature of $h_+$ is that it is multiplicative - that is, if $\gcd(m,n)=1$ then $h_{+}(mn)=h_+(m)h_{+}(n).$

---

Another answer.

We again assume $0\in\mathbb N.$

We will need an explicit bijection $\phi:\mathbb N\to\mathcal P_{\text{Fin}}(\mathbb N),$ where $\mathcal P_{\text{Fin}}(\mathbb N)$ is the set of all finite subsets of $\mathbb N.$

We will also use that if $q\neq 1$ is a positive rational number, then $q$ can be written uniquely as a continued fraction:

$$\left[a_0,a_1,\dots,a_k\right]=a_0+\cfrac1{a_1+\cfrac{1}{\ddots +\cfrac{1}{a_k}}}$$ where $a_0$ is a non-negative integer, the other $a_i$ are positive integers, and $a_k>1.$

We define $g_+:\mathcal P_{\text{Fin}}(\mathbb N)\to\mathbb Q^{+}$ as:

$$\begin{align} &g_+(\emptyset)=1\\ &g_+(\{n\})=n+2\\ &g_+\left(\left\{b_0<b_1<\cdots<b_k\right\}\right)=\left[b_0,b_1-b_0,\dots,b_{k-1}-b_{k-2},b_{k}-b_{k-1}+1\right],\quad k>0 \end{align}$$

The uniqueness of the continued fractions ensures this is a bijection. We had to do some a slight hack to deal with the problem of the empty set.

Then we define $b:\mathbb Z\to \mathbb Q$ similar to before:

$$b(m)=\begin{cases} 0&m=0\\ g_+(\phi(m))&m>0\\ -g_+(\phi(-m))&m<0 \end{cases}$$ And then compose with any bijection $\mathbb N\to\mathbb Z.$ You can use the function $s$ from the previous section. Then $b\circ s$ is a bijection.

This leaves $\phi,$ but every natural number $n$ can be written uniquely in binary, as $n=\sum_{a\in A_n} 2^{a}$ for some finite set $A_n\subseteq \mathbb N.$ Then we can take $\phi(n)=A_n.$

This means that if $n\in\mathbb N$ then $b(2^n)=n+2$ and $b(0)=1.$ Also, $b(1+2^n)=g_+(\{0,n\})=\frac{1}{n+1}.$

$g_+$ is nice because it can be extended to $\mathcal P(\mathbb N)\to\mathbb R^+$ to show a bijection between these two sets, because every irrational number has a unique infinite continued fraction.

Answer 2

We will first create a bijection from $\mathbb{N}$ to $\mathbb{Q}^{+}$ and then use this to create a bijection from $\mathbb{N}$ to $\mathbb{Q}$.

Step One: Let us first define Stern's diatomic series. This process formalizes the Stern-Brocot tree mentioned above.

$a_{1} = 1 \\ a_{2k}=a_{k} \\ a_{2k+1}=a_{k}+a_{k+1}$

To get a feel for this series, let us list out the first few terms.

$a_{1}=1 \\ a_{2}=a_{1}=1 \\ a_{3}=a_{1}+a_{2}=1+1=2 \\ a_{4}=a_{2}=1 \\ a_{5}=a_{2}+a_{3}=1+2=3 \\ a_{6}=a_{3}=2 \\ a_{7}=a_{3}+a_{4}=2+1=3 \\ a_{8}=a_{4}=1$

Now to obtain the $n^{th}$ rational number, we define $f: \mathbb{N} \rightarrow \mathbb{Q}^{+}$, by $f(n)= \dfrac{a_{n}}{a_{n+1}}$.

Let us list out the first few terms.

$f(1)= a_{1}/a_{1+1} = 1/1 \\ f(2)= a_{2}/a_{2+1} = 1/2 \\ f(3)= a_{3}/a_{3+1} = 2/1 \\ f(4)= a_{4}/a_{4+1} = 1/3 \\ f(5)= a_{5}/a_{5+1} = 3/2 \\ f(6)= a_{6}/a_{6+1} = 2/3 \\ f(7)= a_{7}/a_{7+1} = 3/1 $

This function enables us to say that the $6^{th}$ rational number is $2/3$. Moreover, this function is a bijection. For proof of this, see Theorem 5.1 here http://faculty.plattsburgh.edu/sam.northshield/08-0412.pdf.

Since $f$ is a bijection this implies that $f^{-1}$ exists. That means given a rational number we can find the corresponding natural number. For example suppose you have a fraction, say it is $1/4$. Can we determine the $n$ such that $f(n)=1/4$? The answer is a resounding yes. Given a positive rational number, $q \in \mathbb{Q}$, the $n$ such that $f(n)=q$ is found by $n=f^{-1}(q)$. This function, $f^{-1}$, is given as follows:

$f^{-1}(1)=1 \\ f^{-1}(q)= 2f^{-1} \bigg(\dfrac{q}{1-q} \bigg) ~ \text{if} ~ q<1 \\ f^{-1}(q) = 2f^{-1}(q-1)+1 ~\text{if}~ q>1$

As an example, we see from above that $f(5)={3/2}$. Let us plug $(3/2)$ into $f^{-1}$ and see if we get 5.

$f^{-1}(3/2)=2f^{-1} \bigg(\dfrac{3/2}{1-(3/2)} \bigg)+1=2f^{-1} \bigg(\dfrac{1}{2} \bigg)+1.$ A quick calculation yields that $f^{-1} \bigg(\dfrac{1}{2} \bigg)=2$ and so we get $f^{-1}(3/2)=2f^{-1} \bigg(\dfrac{1}{2} \bigg)+1=2(2)+1=5$.

Step Two: We showed there exists a bijection between $\mathbb{N}$ and $\mathbb{Q}^{+}$. We now attempt to show there exists an explicit bijection between $\mathbb{N}$ and $\mathbb{Q}$. Using the work done in Step One, it appears easier to first create a bijection between $\mathbb{Z}$ and $\mathbb{Q}$. The reason for doing so is because we have already created a bijection from the positive integers (natural numbers) to the positive rationals. So it only seems natural that by adding in the negative integers, we can map them to the negative rationals and thus obtain a bijection. We do this as follows:

$$ g(z) = \begin{cases} \dfrac{a_{z}}{a_{z+1}}, & \text{if } z>0 \\ \\ - \dfrac{a_{-z}}{a_{-(z-1)}}, & \text{if } z<0 \\ \\ 0, & \text{if } z=0 \end{cases} $$ where the $a_{i}$ term refers to the $i^{th}$ term in Stern's diatomic series.

We already referenced a proof by Northshield showing that $g(z)=\dfrac{a_{z}}{a_{z+1}}$ if $z>0$ is a bijection from $\mathbb{N} \rightarrow \mathbb{Q}^{+}$. Equivalently, we may write this as $g$ is a bijection from $\mathbb{Z}^{+}$ to $\mathbb{Q}^{+}$ for $z>0$. Now, it follows by the symmetry of the problem that $g(z)=- \dfrac{a_{-z}}{a_{-(z-1)}}$ is a bijection from $\mathbb{Z}^{-}$ to $\mathbb{Q}^{-}$ if $z<0$. That is, $g$ is a bijection between the negative integers and the negative rationals. So we have covered all the positive and negative rationals. The only element in the rationals that is not accounted for is the zero element. So we shall have the integer $0$ mapping to the rational number $0$. However, $g$ is a bijection from the integers to the rationals. We wish to find a bijection from the natural numbers to the rationals. So we shall now define the well-known bijection from the natural numbers to the integers.

$$ h(n) = \begin{cases} \dfrac{n}{2}, & \text{if }n\text{ is even} \\ -\dfrac{n-1}{2}, & \text{if }n\text{ is odd} \end{cases} $$

You may check for yourself that $h$ is a bijection. It follows that $g~\circ~ h: \mathbb{N} \rightarrow \mathbb{Q}$ is a bijection since the composition of two bijections is a bijection. Thus, we have an explicit bijection from $\mathbb{N}$ to $\mathbb{Q}$.

However, given a rational number, can we find what this rational number maps to in the set of natural numbers? Although I do not prove it, the answer is yes and is given by the following piece-wise defined function which is an extension of the function defined in Step One. We first define $g^{-1}: \mathbb{Q} \rightarrow \mathbb{Z}$ as

$$ g^{-1}(q) = \begin{cases} 2f^{-1}(q-1)+1, & \text{if } q>1 \\ 1, & \text{if } q=1 \\ 2f^{-1} \bigg(\dfrac{q}{1-q} \bigg), & \text{if } 0<q<1 \\ 0, & \text{if } q=0 \\ -2 \Bigg(f^{-1} \bigg(\dfrac{-q}{1+q}\bigg) \Bigg), & \text{if } -1<q<0 \\ -1, & \text{if } q=-1 \\ -2(f^{-1}(-q-1)+1), & \text{if } q<-1 \end{cases} $$

We now define the function $h^{-1}: \mathbb{Z} \rightarrow \mathbb{N}$ as follows:

$$ h^{-1}(z)= \begin{cases} 2z, & \text{if } z>0 \\ 1, & \text{if } z=0 \\ -2z-1, & \text{if } z<0 \\ \end{cases} $$

Then $h^{-1} \circ g^{-1}: \mathbb{Q} \rightarrow \mathbb{N}$ is the bijection we are looking for.

Answer 3

Recently I was reading some papers by Don Zagier and found this one most interesting. Here, you can get not only a satisfactory proof of the bijection, but also you will have the notion of the rational number immediately after, or before, a given number, which we don't have in Cantor's proof.

Theorem:

The map $$S(x)=\frac{1}{2\lfloor x\rfloor-x+1}$$ has the property that, among the sequence $S(0),S(S(0),S(S(S(0)),\cdots $ every positive rational numbers appears once and only once.

Therefore if we write $S^n(x)$ for $n^{th}$ iterate of $S$, then we obtain an explicit bijection $F:\mathbb{N}\to \mathbb{Q}^{+}$ by $F(n)=S^n(0) $. The proof is explained in the link I have mentioned above.

Answer 4

Preliminaries

I will be using the Continued Fraction conception. Firstly, let us consider only rationals that are less than 1. So $$q < 1, \quad q\in\mathbb{Q}$$ So every rational $q$ can be written as a continued fraction: $$q = \cfrac{1}{a_1 + \cfrac{1}{a_2 +\cfrac{1}{a_3 + ...}}} := [a_1, a_2, a_3, ...]$$ Note that none of the $a_i$ is zero and for every $q\in\mathbb{Q}$ its q.f. is of the finite length. Also note that we're using only that kind of q.f.'s in which all the numerators are 1's.

Formula

Let us construct a bijection $\Phi$ between rationals and naturals as follows: $$\Phi: q \mapsto \prod_{i=1}^{n_q}p_{i}^{a_i - 1},$$ where $n_q$ is the length of q.f. for $q$ and $p_i$ is $i$th prime number. The inverse is straightforward.

Example

$$\Phi\Big(\frac{30}{43}\Big) = 2^03^15^27^3 = 25725$$ This is because $$\frac{30}{43} = \cfrac{1}{1+\cfrac{1}{2+\cfrac{1}{3+\cfrac{1}{4}}}} := [1,2,3,4]$$ And vice-versa: $$\Phi^{-1}(225) = \frac{10}{13} = \cfrac{1}{1+\cfrac{1}{3+\cfrac{1}{3}}}$$ This is because $$225 = 2^03^25^2$$

---

Of course this works iff there is bijection between those kind of continued fractions and rationals. But it is not too hard to prove.

---

P.S. I feel that I'm missing something here. Please, verify.

Answer 5

The method used here cobbles together parts and pieces of the Euler's totient function to create our sequence that bijectively covers all the rational numbers.

The function is implemented using the python programming language, but the interested reader can figure out what is happening by inspecting the output.

Here is the program:

#--------*---------*---------*---------*---------*---------*---------*---------*
# Desc: Define a bijection of natural numbers to the rational numbers
#--------*---------*---------*---------*---------*---------*---------*---------*

import sys
import fractions

def moreTicks(curTick):
    for k in range(1, curTick):
        if fractions.gcd(curTick, k) == 1:
            moreTicksList.append(fractions.Fraction(k, curTick))
    return curTick + 1


#--------*---------*---------*---------*---------*---------*---------*---------#
while True:#                       M A I N L I N E                             #
#--------*---------*---------*---------*---------*---------*---------*---------#
#                                  # initialize state of function machine
    step = 0
    negSide = 0
    posSide = 0
    curTick = 2
    phiList = []
    print(0, ', ', end='')

    while True:
        #print('expand by phi(n) count on working range')
        moreTicksList = []
        curTick = moreTicks(curTick)
        for i in range(negSide, posSide + 1):
            for f in moreTicksList:
                print(f + fractions.Fraction(i, 1), ', ', end='')
        for f in moreTicksList:
            phiList.append(f)
        #print("add phiList to '-' side")
        negSide = negSide - 1
        print(negSide, ', ', end='')
        for f in phiList:
            print(f + fractions.Fraction(negSide, 1), ', ', end='')
        #print("add phiList to '+' side")
        posSide = posSide + 1
        print(posSide, ', ', end='')
        for f in phiList:
            print(f + fractions.Fraction(posSide, 1), ', ', end='')
        step = step + 1
        if step == 7:
            print('...', end='')
            sys.exit()

Here is the output sequence (you can use the slider to see further out):

0 , 1/2 , -1 , -1/2 , 1 , 3/2 , -2/3 , -1/3 , 1/3 , 2/3 , 4/3 , 5/3 , -2 , -3/2 , -5/3 , -4/3 , 2 , 5/2 , 7/3 , 8/3 , -7/4 , -5/4 , -3/4 , -1/4 , 1/4 , 3/4 , 5/4 , 7/4 , 9/4 , 11/4 , -3 , -5/2 , -8/3 , -7/3 , -11/4 , -9/4 , 3 , 7/2 , 10/3 , 11/3 , 13/4 , 15/4 , -14/5 , -13/5 , -12/5 , -11/5 , -9/5 , -8/5 , -7/5 , -6/5 , -4/5 , -3/5 , -2/5 , -1/5 , 1/5 , 2/5 , 3/5 , 4/5 , 6/5 , 7/5 , 8/5 , 9/5 , 11/5 , 12/5 , 13/5 , 14/5 , 16/5 , 17/5 , 18/5 , 19/5 , -4 , -7/2 , -11/3 , -10/3 , -15/4 , -13/4 , -19/5 , -18/5 , -17/5 , -16/5 , 4 , 9/2 , 13/3 , 14/3 , 17/4 , 19/4 , 21/5 , 22/5 , 23/5 , 24/5 , -23/6 , -19/6 , -17/6 , -13/6 , -11/6 , -7/6 , -5/6 , -1/6 , 1/6 , 5/6 , 7/6 , 11/6 , 13/6 , 17/6 , 19/6 , 23/6 , 25/6 , 29/6 , -5 , -9/2 , -14/3 , -13/3 , -19/4 , -17/4 , -24/5 , -23/5 , -22/5 , -21/5 , -29/6 , -25/6 , 5 , 11/2 , 16/3 , 17/3 , 21/4 , 23/4 , 26/5 , 27/5 , 28/5 , 29/5 , 31/6 , 35/6 , -34/7 , -33/7 , -32/7 , -31/7 , -30/7 , -29/7 , -27/7 , -26/7 , -25/7 , -24/7 , -23/7 , -22/7 , -20/7 , -19/7 , -18/7 , -17/7 , -16/7 , -15/7 , -13/7 , -12/7 , -11/7 , -10/7 , -9/7 , -8/7 , -6/7 , -5/7 , -4/7 , -3/7 , -2/7 , -1/7 , 1/7 , 2/7 , 3/7 , 4/7 , 5/7 , 6/7 , 8/7 , 9/7 , 10/7 , 11/7 , 12/7 , 13/7 , 15/7 , 16/7 , 17/7 , 18/7 , 19/7 , 20/7 , 22/7 , 23/7 , 24/7 , 25/7 , 26/7 , 27/7 , 29/7 , 30/7 , 31/7 , 32/7 , 33/7 , 34/7 , 36/7 , 37/7 , 38/7 , 39/7 , 40/7 , 41/7 , -6 , -11/2 , -17/3 , -16/3 , -23/4 , -21/4 , -29/5 , -28/5 , -27/5 , -26/5 , -35/6 , -31/6 , -41/7 , -40/7 , -39/7 , -38/7 , -37/7 , -36/7 , 6 , 13/2 , 19/3 , 20/3 , 25/4 , 27/4 , 31/5 , 32/5 , 33/5 , 34/5 , 37/6 , 41/6 , 43/7 , 44/7 , 45/7 , 46/7 , 47/7 , 48/7 , -47/8 , -45/8 , -43/8 , -41/8 , -39/8 , -37/8 , -35/8 , -33/8 , -31/8 , -29/8 , -27/8 , -25/8 , -23/8 , -21/8 , -19/8 , -17/8 , -15/8 , -13/8 , -11/8 , -9/8 , -7/8 , -5/8 , -3/8 , -1/8 , 1/8 , 3/8 , 5/8 , 7/8 , 9/8 , 11/8 , 13/8 , 15/8 , 17/8 , 19/8 , 21/8 , 23/8 , 25/8 , 27/8 , 29/8 , 31/8 , 33/8 , 35/8 , 37/8 , 39/8 , 41/8 , 43/8 , 45/8 , 47/8 , 49/8 , 51/8 , 53/8 , 55/8 , -7 , -13/2 , -20/3 , -19/3 , -27/4 , -25/4 , -34/5 , -33/5 , -32/5 , -31/5 , -41/6 , -37/6 , -48/7 , -47/7 , -46/7 , -45/7 , -44/7 , -43/7 , -55/8 , -53/8 , -51/8 , -49/8 , 7 , 15/2 , 22/3 , 23/3 , 29/4 , 31/4 , 36/5 , 37/5 , 38/5 , 39/5 , 43/6 , 47/6 , 50/7 , 51/7 , 52/7 , 53/7 , 54/7 , 55/7 , 57/8 , 59/8 , 61/8 , 63/8 , ...

---

The sequence 'calibrates' the rational number 'tick marks' on our ideal 'measuring rod'.

Answer 6

Set $\Bbb N = \{1,2,3,4,\dots\}$.

Here we will define a bijective mapping between $\Bbb N$ and the subset of rational numbers

$\quad \Bbb Q_{\gt 0}^{\lt 1} = \{q \in \Bbb Q \mid 0 \lt q \lt 1\}$

For integer $n \ge 1$ define the set

$\tag 1 F_n = \{s/t\in \Bbb Q \mid [s, t \in \Bbb N] \land [t \le n] \land [s \lt t\}]$

We have a chain of inclusions

$\tag 2 \emptyset = F_1 \subset F_2 \subset F_3 \subset \dots \subset F_k \subset \dots $

and denote the union of these sets by $F$; observe that $F = \Bbb Q_{\gt 0}^{\lt 1}$.

Let the number of elements in the set $F_k$ be denoted by $f_k$.

If $k \gt 1$ let $G_k = F_k \setminus F_{k-1}$; observe that $G_k$ has an ordering relation $\le$ defined on it.

We define a function $\Gamma: \Bbb N \to F$ by the specification

$\quad$ Given $m \in \Bbb N$
$\quad$ Find $k \in \Bbb N$ such that $f_k \lt m \le f_{k+1}$
$\quad$ Set $\Gamma(m)$ to the

$\tag 3 [m-f_k]^\text{-th} \text{ element of } G_{k+1}$

Exercise: Show that $\Gamma$ is a well defined function that puts the sets into a $\text{1:1 correspondence}$.

See also the wikipedia article Farey sequence.

Answer 7

This is a bijection between the Stern-Brocot tree and the tree of Natural numbers. Every left node is given by $ L_n = [2 P_n ] $ and every right one by $ R_n= [2 P_n +1 ]$ where $P_n $ is the value of the parent node and $P_0=[1]$. We have the sequence of transformations $ P_n \rightarrow [ L_n , R_n ]$, $L_n \rightarrow P_{n+1}$, $R_n \rightarrow P^\prime_{n+1}$ .

In list notation for the tree (count the brackets) this is

$$ n = 1 \mapsto [1,[2],[3]] $$

$$n = 2 \mapsto [1,[2,[4], [5]], [3,[6], [7]]] $$ $$ n = 3 \mapsto [1,[2,[4,[8],[9]],[5,[10],[11]]],[3,[6,[12],[13]],[7,[14],[15]]]] $$ and so on.

Answer 8

I would like to make two comments, both in the direction of dynamics.

---

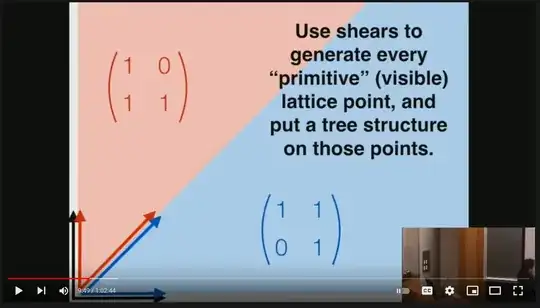
1. Consider the matrices $L=\begin{pmatrix}1&0\\1&1\end{pmatrix}$ and $R=\begin{pmatrix}1&1\\0&1\end{pmatrix}$ which act as shears on the first quadrant $\mathbb{R}_{\geq0}^2$:

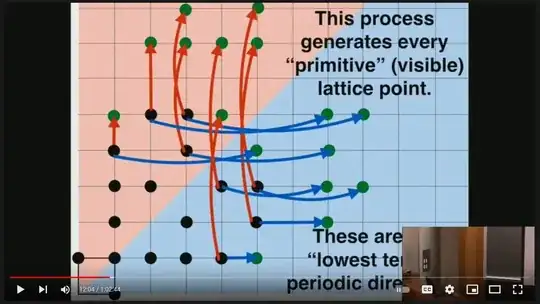
Thinking of nonnegative rational numbers as (slopes of rays from the origin through) integer points in $\mathbb{R}^2_{\geq0}$, successive iterates of $L$ and $R$ count $\mathbb{Q}_{\geq0}$:

(A rigorous way of saying/proving this is that $L$ and $R$ freely generate the monoid $\operatorname{SL}(2,\mathbb{Z}_{\geq0})$ of $2\times 2$ matrices with nonnegative integer entries and determinant $1$.)

Choosing an ordering on binary words now produces a bijection $\mathbb{Z}_{\geq0}\to\mathbb{Q}_{\geq0}$. Alternatively one can use some geometric ordering on the "visible points" (e.g. according to polar coordinates).

I have taken the above screenshots from D. Davis' talk "Periodic paths on the pentagon: Swarthmore College Math/Stat Colloquium" (https://youtu.be/5kyundHawJ8; other recordings of the talk seems to be also available); the associated paper is "Periodic paths on the pentagon, double pentagon and golden L" (https://arxiv.org/abs/1810.11310) by Davis & Lellièvre. (They adapt this counting procedure to enumerate closed orbits of billiards on the double pentagon; from the dynamical point of view the above procedure counts the periodic translation trajectories on the square torus or square billiard table.)

Of course this is nothing but the (...-Kepler-...-) Calkin-Wilf tree mentioned above in disguise; indeed, $L(z)$ and $R(z)$ are the two offsprings of $z$.

---

2. The second comment is about the Newman map mentioned above, which is defined by

$$N:[0,\infty]\to[0,\infty],\,\, x\mapsto \begin{cases}0 &\text{, if }x=\infty\\ \dfrac{1}{1-\{x\}+\lfloor x\rfloor}&\text{, otherwise}\end{cases},$$

where $\lfloor x\rfloor$ is the floor of $x$ and $\{x\}=x-\lfloor x\rfloor$ is the fractional part of $x$.

$N$ is a bimeasurable bijection that preserves $\mathbb{Q}_{>0}$. As mentioned above, the orbit of $0$ under $N$ is in one-to-one correspondence with nonnegative rational numbers. Bonanno & Isola, in their paper "Orderings of the rationals and dynamical systems" (https://arxiv.org/abs/0805.2178, Thm.2.3 on p.176), proved that up to a change of coordinates $N$ is the dyadic odometer ( = Von Neumann-Kakutani adding machine) (see e.g. What are the applications of dynamical odometers? or Unclear construction in a paper of Ornstein and Weiss):

Theorem (Bonanno-Isola): Put $\Phi: [0,\infty]\to [0,1], x\mapsto\begin{cases}1&\text{, if }x=\infty\\ \dfrac{x}{x+1}&\text{ otherwise}\end{cases}$, $S=\Phi\circ N\circ \Phi^{-1}$, $?:[0,1]\to[0,1]$ be the (restriction of the) Minkowski question mark function (which is a homeomorphism that is not absolutely continuous) (see e.g. Intuition in understanding Minkowski question mark ?(x) function, Academic reference concerning Minkowski's question mark function), $T$ be the odometer. Then:

(The coordinate change $\Phi$ is also not accidental; it transforms the Stern-Brocot tree into the Farey tree.)

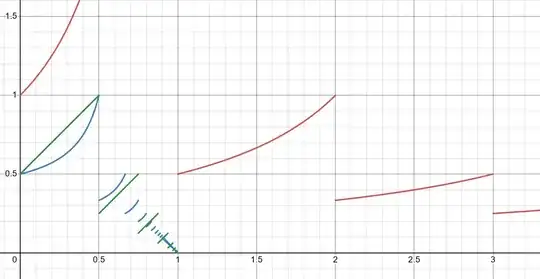
Here is a humble graph (https://www.desmos.com/calculator/rg6xwg5qj1), where $N$ is red, $S$ is blue and (an approximation of) $T$ is green:

Thus we have another geometric way of enumerating the rational numbers using the odometer ($0$ is sent to $0$ by $?\circ \Phi$). Arguably it's easier to iterate $T$ than $N$.

Answer 9

The following is not a rigorous mathematical proof but rather a sketch of an idea.

First, represent any rational number $\frac{a}{b}$ with $a, b\in\mathbb{N}$, $b\ne 0$ by the order pair $(a, b)$. In this way, $\mathbb{Q}$ can be represented by the set of order pairs:

$$ \begin{align} (1, 1),\ (2&, 1),\ ..., (k, 1),\ ...\\ (2, 1),\ (2&, 2),\ ..., (k, 2),\ ...\\ &\vdots\\ (n, 1),\ (n&, 2),\ ..., (k, n),\ ...\\ &\vdots\\ \end{align} $$

Denote by $R_1$ the set in the first row in the table, $R_2$ the second row, $R_k$ for the $k$-th row. Then, it's easy to see that there's a bijection from $\mathbb{N}\to R_i$, for all $i\in\mathbb{N}_+$.

Let $N_0=\{2n: n\in\mathbb{N}\}$, $N_1=\{2n+1: n\in\mathbb{N}\}$. It follows that $\mathbb{N}=N_0\bigcup N_1$. Observe that the mappings $\mathscr{i}: n\to n$, $f: 2n\mapsto n$ and $g: 2n+1\mapsto n$ are all bijective. In other words, the mappings $\mathscr{i}: \mathbb{N}\to \mathbb{N}$, $f: N_0\to\mathbb{N}$ and $g: N_1\to\mathbb{N}$ are bijective. Thus, we can create a bijection $h_1: \mathbb{N}\to \mathbb{N}\sqcup(N_0\cup N_1)$, where $\sqcup$ denotes the disjoint union, by combining three bijections $\mathscr{i}:\mathbb{N}\to N_0\cup N_1$ (note: $N_0\cup N_1=\mathbb{N}$), $f: N_0\to\mathbb{N}$ and $g: N_1\to (N_0\cup N_1)$.

Next, create a bijection $r_1: \mathbb{N}\to R_1\cup (N_0\cup N_1)$ by connection $h_1$ and $r_1': \mathbb{N}\to R_1$. Now, rewrite $r_1: \mathbb{N}\to R_1\cup\mathbb{N}$ and repeat the above process indefinitely but starting from the next row. We then obtain a bijection that maps $\mathbb{N}$ to every row in the table, or a bijective mapping from $\mathbb{N}\to\mathbb{Q}$.