There are 3 definitions of Minkowski function:
1) If $[a_0; a_1, ...]$ is a continuous function representation of n
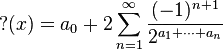
2) Consider the different ways of interpreting an infinite string of bits beginning with 0 as a real number in [0,1]. One obvious way to interpret such a string is to place a binary point after the first 0 and read the string as a binary expansion. Another interpretation views a string as the continued fraction $[0; a_1, a_2, … ]$, where the integers $a_i$ are the run lengths in a run-length encoding of the string. The effect of the question mark function on [0,1] can then be understood as mapping the second interpretation of a string to the first interpretation of the same string. (Wiki)
3) $?(x) = \lim_{n -> + \infty} \frac{B_n \cap [0, x]}{2^n + 1}$, where $B_n$ is the nth Stern-Brocot series.
I think I understand the definitions separately, but I have problems mapping them to each other, especially second to third.