5

By definition, a set $S$ is called countable if there exists an bijective function $f$ from $S$ to the natural numbers $N$.

If we take a function $g\colon\mathbb{Z\times N\to Q}$ given by $g(m, n) = \frac{m}{ n} $ to "construct" rational numbers, $g$ would only be a surjection from the countable set $\mathbb{Z\times N}$ to $\mathbb Q$. It's not injective, or is it?

Asaf Karagila
  • 393,674
user1511417
  • 907
  • 3
    If there's a surjection then there is an injection. You may need here the Axiom of Choice, though. – Timbuc Feb 06 '15 at 10:57
  • I don't agree. A function can be surjective and not injective. – user1511417 Feb 06 '15 at 11:03
  • I didn't say otherwise: I wrote that if you have a surjection then you can build, with AC, and injection, not that the surjection has to be also an injection. – Timbuc Feb 06 '15 at 11:10
  • @user1511417 You got the tricky part. It is not just the same case like counting $\mathbb{N}^2$. – mvw Feb 06 '15 at 11:20
  • 1
    @Timbuc: Why involve the axiom of choice, where all the sets you deal with are countable? – Asaf Karagila Feb 06 '15 at 11:22
  • @AsafKaragila That has a very simple answer: I really don't know. First, I feel not that uncomfortable using big weapons to kill flies. Second, I love AC as it's made my mathematical life very nice. Third, I really don't know how to begin constructing an injection out of an injection: I thought something like "choose (here kicks in AC in my non-set-theoretical mind!) an element $;(a,b)\in f^{-1}(q);,;;q\in\Bbb Q;$ and...etc." Why being countable makes AC unnecessary isn't very clear to me. Thanks. – Timbuc Feb 06 '15 at 11:26
  • @Timbuc: Because you can enumerate the domain (or otherwise well-order it) and pick the smallest element (in the enumeration) in the preimage. – Asaf Karagila Feb 06 '15 at 11:29
  • Oh, rats: that's simple. Thanks @AsafKaragila. I gather that it doesn't matter whether the set is finite or infinite, it is possible to choose from a countable list because of the well ordering of the naturals? – Timbuc Feb 06 '15 at 11:34
  • See as well Explicit bijections – mvw Feb 06 '15 at 11:51

6 Answers6

9

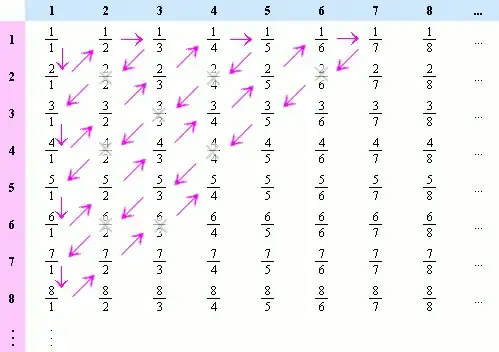
Explicit bijections are overrated.

We can prove the following three things (without the axiom of choice, which has been mentioned in the comments):

  1. If $A\subseteq\Bbb N$ then it is either finite or countably infinite.
  2. If $f\colon\Bbb N\to X$ is surjective, then $X$ is finite or countably infinite.
  3. There is a surjection from $\Bbb N$ onto $\Bbb Q$.

The first proof is quite easy, we simply start to enumerate $A$ according to the order induced from the usual order of the the natural numbers. Either we "finish" the set, in which case it's finite, or the enumeration produces a bijection of $A$ with $\Bbb N$.

The second proof is also easy, since the function is a surjection, every $x\in X$ has a least $n\in\Bbb N$ such that $f(n)=x$. This minimal $n$ is unique, so we defined an injection from $X$ into $\Bbb N$, which is a bijection with a subset of $\Bbb N$. By the first claim, $X$ is finite or countably infinite.

The last proof is also not difficult. First write a surjection of $\Bbb N$ onto $\Bbb{N\times N}$ and a surjection from $\Bbb N$ onto $\Bbb Z\setminus\{0\}$, compose them to a surjection from $\Bbb N$ onto $\Bbb{N\times (Z\setminus\{0\})}$. Then you the surjection you have defined, $(n,m)\mapsto\frac nm$.

Now we can conclude the fourth statement:

  1. $\Bbb Q$ is countably infinite.

Of course $\Bbb Q$ is not finite, and since there is a surjection from $\Bbb N$ onto $\Bbb Q$, the claim is proved.

Asaf Karagila
  • 393,674
2

Here's an intuitive but very helpful to understand picture. enter image description here

Andrei Rykhalski
  • 1,325
  • 9
  • 14
1

You are correct. In fact, this is not the function used to count rational numbers.

Imagine listing all of those numbers excluding the ones in which the fraction can be simplified.

A possible bijection could be that function that gives the position of the rational number in that list. Since the list contains each rational number, the function is surjective. But each number has a different position in the list: hence, the function is surjective.

This is an "intuitive" point of view. If you want a more formal demonstration here it is:

Define the mapping $\psi: \mathbb Q \rightarrow \mathbb Z \times \mathbb N$ such that for every $\frac{m}{n} \in \mathbb Q$ in canonical form $\psi(\frac{m}{n})=(m,n)$

Then $\psi$ is clearly injective. From the fact that cartesian product of countably infinite sets is countably infinite, $\mathbb Z \times \mathbb N$ is countable. Because the domain of injection to a countable set is countable, $\mathbb Q$ is countable.

Lonidard
  • 4,253
  • That is not the bijection used for anything: that function simply is not a bijection. – Timbuc Feb 06 '15 at 11:13
  • Timbuc, you are right. I meant function. Thanks for the comment, I'll edit the post – Lonidard Feb 06 '15 at 11:14
  • That's plausible for me. Thanks. For a bijection it's a prerequisite that $Q$ is in its canonical form. – user1511417 Feb 06 '15 at 11:20
  • Exactly. In most of the proofs I've seen, this is part of the requirements. – Lonidard Feb 06 '15 at 11:26
  • 1
    Wait, how is $\psi$ surjective? $(2,4)$ is not in its image, and if it is then $(1,2)$ is not, and if it is, then it's not a function! – Asaf Karagila Feb 06 '15 at 11:31
  • Asaf, you are correct. I must invoke the fact that domain of injection to countable set is countable. Quite a stupid mistake – Lonidard Feb 06 '15 at 11:36
  • There's also a gap here, which I explain in my answer. You essentially claim that it suffices to show a surjection from a countable set onto $\Bbb Q$, which is true, but it is true because we can prove that an infinite subset of a countable set is countably infinite; therefore there is a bijection between $\Bbb Q$ and a set which we can prove to be countably infinite. – Asaf Karagila Feb 06 '15 at 11:44
  • It seems quite obvious to me, actually. If $A$ is a subset of $B$ then $B\geA$. If this was not true, B would be a proper a subset of A, contradicting our hypothesis. – Lonidard Feb 06 '15 at 12:07
  • Yes, but why isn't there some intermediate infinite cardinality? Something smaller than $\aleph_0$? – Asaf Karagila Feb 06 '15 at 12:13
  • I am not proving that $|\mathbb N|=|\mathbb Q|$. I am proving that $\mathbb Q$ is countable, as requested. – Lonidard Feb 06 '15 at 12:19
0

Consider the plane $\mathbb Z\times\mathbb Z$. Clearly you can fill it by spiraling from the origin. Avoid counting the undefined fractions and those already seen before (after simplification).

  • I preferred to work in $\mathbb Z\times\mathbb Z$ as the trajectory can be described with just one word. –  Feb 06 '15 at 11:37
0

The Farey sequence gives a bijection between the nonnegative rationals and $\mathbb{N}$.
Step 0: Start with two numbers $\frac01,\frac10$ ($\frac10$ is just a place-holder.) $\frac01$ is rational number $1$.
Step N: between consecutive numbers$\frac{a}{b},\frac{c}{d}$, write $\frac{a+c}{b+d}$ These are rationals number $2^{N-1}+1$ to number $2^N$
The sequence starts
$$\frac01,\frac10\\ \frac01,\frac11,\frac10\\ \frac01,\frac12,\frac11,\frac21,\frac10\\ \frac01,\frac13,\frac12,\frac23,\frac11,\frac32,\frac21,\frac31,\frac10$$
To include the negatives, put the negative numbers in the even positions and positive numbers in the odd positions.

Empy2
  • 50,853
0

Let us enumerate the elements of $\{0\}\cup\{1,2,...\}\!\!\times\!\!\{1,2,...\}\!\!\times\!\!\{+,-\}$. Start with $0$. Then, for given $n$, list all $2n$ elements $(j,k,\pm)$ such that $j+k=n$, successively in the order $(1,n-1),...,(n,1)$, with $+$ signs attached, followed by the same elements with $-$ signs. Do this consecutively for $n=1,2,...$. This list is countable. Now run through the list in order and delete any element $(l,m,\pm)$ for which there was an earlier-occurring element $(j,k,\pm)$ (with the same sign) such that $j/k=l/m$. Now we have a countable list that is in one-to-one correspondence with the rational numbers $\Bbb Q$: namely, $(j,k,\pm)$ corresponds to $q\in\Bbb Q$ if and only the signs are the same and $j/k=q$, with the initial $0$ corresponding to the $0$ in $\Bbb Q$.

John Bentin
  • 18,454