15

I have to calculate $$\int_0^\infty\frac{\log x dx}{x^2-1},$$

and the hint is to integrate $\frac{\log z}{z^2-1}$ over the boundary of the domain $$\{z\,:\,r<|z|<R,\,\Re (z)>0,\,\Im (z)>0\}.$$

I don't understand. The boundary of this domain has a pole of the integrand in it, doesn't it? Doesn't it make this method useless?

Bartek
  • 6,265

5 Answers5

13

$$\int_0^{\infty} \dfrac{\log(x)}{1-x^2} dx = \int_0^{1} \dfrac{\log(x)}{1-x^2} dx + \int_1^{\infty} \dfrac{\log(x)}{1-x^2} dx$$ $$\int_1^{\infty} \dfrac{\log(x)}{1-x^2} dx = \int_1^0 \dfrac{\log(1/x)}{1-1/x^2} \left(-\dfrac{dx}{x^2} \right) = \int_1^0 \dfrac{\log(x)}{x^2-1} dx=\int_0^1 \dfrac{\log(x)}{1-x^2}dx$$ Hence, $$\int_0^{\infty} \dfrac{\log(x)}{1-x^2} dx = 2\int_0^{1} \dfrac{\log(x)}{1-x^2} dx$$ Now note that in $(0,1)$, we have $$\dfrac1{1-x^2}= \sum_{k=0}^{\infty} x^{2k} \,\,\,\,\,\,\,\, \text{(Geometric/Taylor series)}$$ $$\int_0^{1} \dfrac{\log(x)}{1-x^2} dx = \int_0^1 \left( \sum_{k=0}^{\infty} x^{2k} \right)\log(x) dx = \sum_{k=0}^{\infty} \int_0^1 x^{2k} \log(x) dx = -\sum_{k=0}^{\infty}\dfrac1{(2k+1)^2}$$ (If $\displaystyle \int_0^{1} \dfrac{\log(x)}{1-x^2} dx$, exists, we can afford to swap the integral and summation thanks, to dominated convergence theorem.)

Hence, $$\int_0^{\infty} \dfrac{\log(x)}{1-x^2} dx = - \sum_{k=0}^{\infty} \dfrac2{(2k+1)^2} =-\dfrac{\pi^2}4$$ Your integral is $$\int_0^{\infty} \dfrac{\log(x)}{x^2-1} dx = - \int_0^{\infty} \dfrac{\log(x)}{1-x^2} dx = \dfrac{\pi^2}4$$

  • Thank you for the answer. I don't understand what's happening in your solution from the point where the first summation symbol appears. Could you explain that line? – Bartek Feb 03 '13 at 22:20
  • @Bartek Have added couple of lines. Is it clear now? –  Feb 03 '13 at 22:23
  • Thank you, I understand the geometric series thing now. But where does $\pi^2/4$ come from? – Bartek Feb 03 '13 at 22:25
  • @Bartek We have $$\zeta(2) = 1 + \dfrac1{2^2} + \dfrac1{3^2} + \cdots = \dfrac{\pi^2}6$$ Hence, $$\zeta(2) = \left(1 + \dfrac1{3^2} + \dfrac1{5^2} + \cdots \right) + \left(\dfrac1{2^2} + \dfrac1{4^2} + \dfrac1{6^2} + \cdots \right)$$ i.e.$$\zeta(2) = \left(1 + \dfrac1{3^2} + \dfrac1{5^2} + \cdots \right) + \dfrac{\zeta(2)}4$$ i.e.$$ \left(1 + \dfrac1{3^2} + \dfrac1{5^2} + \cdots \right) = \dfrac{3\zeta(2)}4 = \dfrac34 \times \dfrac{\pi^2}6 = \dfrac{\pi^2}8$$ –  Feb 03 '13 at 22:27
  • Thank you very much! I understand now. I will look at the proofs you've linked to. I still wonder what the hint means, but I see that your solution is good and quick. – Bartek Feb 03 '13 at 22:35
9

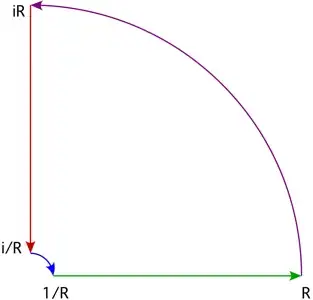
Following the hint, let $$f(z) = \frac{\log z}{z^2-1}$$ where $\log$ is the principal branch of the complex logarithm. Since $z=1$ is a simple zero for $z^2-1$ and $\log 1 = 0$, the function $f$ has a removable singularity at $z=1$.

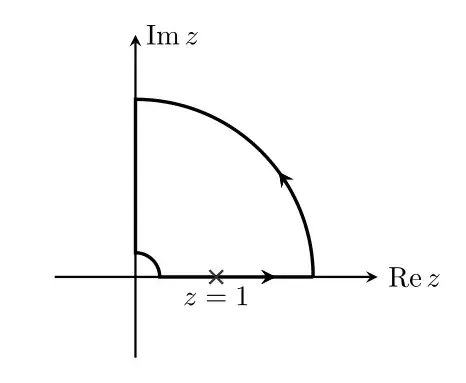
enter image description here

Integrate $f$ along the contour. It's easy to check (using standard estimates) that the integral of $f$ along the two quarter-circles tend to $0$ as $R \to \infty$ and $r \to 0^+$. The function $f$ is holomorphic on and inside the contour, so Cauchy's integral theorem will give you (after passing to the limit)

$$ \int_0^\infty \frac{\log x}{x^2-1}\,dx - \int_0^\infty \frac{\log it}{(it)^2-1}\,i\,dt = 0 $$ i.e. $$ \int_0^\infty \frac{\log x}{x^2-1}\,dx = -\int_0^\infty \frac{\log t + i\pi/2}{t^2+1}\,i \,dt = \frac{\pi^2}{4} \tag{*}$$

using $\int_0^\infty \frac{\log t}{1+t^2}\,dt = 0$ (see e.g. this question) and the elementary $\int_0^\infty \frac{1}{1+t^2}\,dt = \frac{\pi}{2}$.

Added As pointed out by robjohn, just take the real part of (*) to finish it off.

Community
  • 1
mrf
  • 43,639
  • My answer is similar, but I wanted to bring out extra information available within the equations. If you feel it is too close, I can delete mine. – robjohn Feb 04 '13 at 08:58
  • @robjohn Nah, leave it up. I should have thought of just taking the real part, but I guess I was distracted trying to find a duplicate and only finding the $\log x/(1+x^2)$-integral. – mrf Feb 04 '13 at 09:00
7

While similar to mrf's answer, this is simplified by equating the real and imaginary parts of $(3)$.

Since there are no singularities inside the contour in the hint, we get $$ \oint\frac{\log(z)}{z^2-1}\mathrm{d}z=0\tag{1} $$ Breaking the countour into four pieces as follows

$\hspace{4.5cm}$enter image description here

$(1)$ and the triangle inequality yield $$ \left|\color{#00A000}{\int_{1/R}^R\frac{\log(x)}{x^2-1}\mathrm{d}x} \color{#C00000}{-\int_{1/R}^R\frac{\log(ix)}{-x^2-1}\mathrm{d}ix}\right| \le\color{#0000FF}{\frac{\log(R)+\pi/2}{1-1/R^2}\frac{\pi}{2R}} +\color{#800080}{\frac{\log(R)+\pi/2}{R^2-1}\frac{\pi R}{2}}\tag{2} $$ which, as $R\to\infty$, guarantees $$ \begin{align} \int_0^\infty\frac{\log(x)}{x^2-1}\mathrm{d}x &=\int_0^\infty\frac{\log(ix)}{-x^2-1}\mathrm{d}ix\\ &=-i\int_0^\infty\frac{\log(x)}{x^2+1}\mathrm{d}x +\frac\pi2\int_0^\infty\frac1{x^2+1}\mathrm{d}x\tag{3} \end{align} $$ By equating the real and imaginary parts in $(3)$, we get not only the desired answer $$ \int_0^\infty\frac{\log(x)}{x^2-1}\mathrm{d}x=\frac{\pi^2}{4}\tag{4} $$ but also $$ \int_0^\infty\frac{\log(x)}{x^2+1}\mathrm{d}x=0\tag{5} $$

robjohn
  • 345,667
  • I didn't get the right side of (2), can you explain this for me? – Mauro Jun 03 '15 at 11:47
  • 1
    On the blue arc, the triangle inequality says $$\begin{align}|\log(z)| &=|-\log(R)+i\arg(z)|\ &\le\log(R)+\pi/2\end{align}$$ and $$\begin{align}|z^2-1| &\ge1-|z^2|\ &=1-1/R^2\end{align}$$ and the length of the arc is $\dfrac\pi{2R}$. On the purple arc $$\begin{align}|\log(z)| &=|\log(R)+i\arg(z)|\ &\le\log(R)+\pi/2\end{align}$$ and $$\begin{align}|z^2-1| &\ge|z^2|-1\ &=R^2-1\end{align}$$ and the length of the arc is $\dfrac{\pi R}2$. – robjohn Jun 03 '15 at 12:28
2

Note

$$I(a)=\int_0^\infty\frac{\ln x}{(x+1)(x+a)}dx\overset{x\to\frac a x} = \frac{1}{2}\int_0^\infty\frac{\ln a}{(x+1)(x+a)}dx= \frac{\ln^2a}{2(a-1)} $$ Then $$\int_0^\infty\frac{\ln x}{x^2-1}dx=I(-1)=-\frac14 [\ln(e^{i\pi})]^2=\frac{\pi^2}4 $$

Quanto
  • 97,352
2

This is somewhat similar to the answer by user17762, but instead I make use of the dilogarithm function, which can be related to the infinite series used in that answer:

$$ \operatorname{Li_2}(z) = -\int_0^z \frac{\ln(1-t)}{t} dt $$

$$ \int_0^\infty \frac{\log x}{x^2-1} dx = \int_0^1 \frac{\log x}{x^2-1} dx + \int_1^\infty \frac{\log x}{x^2-1} dx $$

Substituting $u=\frac{1}{x}$ into the second integral yields:

$$ \int_1^\infty \frac{\log x}{x^2-1} dx = \int_0^1 \frac{\log x}{x^2-1} dx $$ $$ \int_0^\infty \frac{\log x}{x^2-1} dx = 2 \int_0^1 \frac{\log x}{x^2-1} dx $$

Now substituting $u=\frac{1-x}{1+x}$ yields:

\begin{align*} \int_0^\infty \frac{\log x}{x^2-1} dx = 2 \int_0^1 \frac{\log x}{x^2-1} dx &= -\int_0^1 \frac{\log (1-u)}{u} du + \int_0^1 \frac{\log (1+u)}{u} du \\ &= -\int_0^1 \frac{\log (1-u)}{u} du + \int_0^{-1} \frac{\log (1-v)}{v} dv \\ &= \operatorname{Li_2}(1) - \operatorname{Li_2}(-1) \\ &= \frac{\pi^2}{6} - \frac{-\pi^2}{12} \\ &= \frac{\pi^2}{4} \end{align*}

Community
  • 1
Tyler Streeter
  • 559