Are the integration contours of this improper integral properly selected?

Question

I have been recently trying to review some topics on improper integrals. The Integral I am trying to solve is:
$$ \int_0^\infty {log(x) \over x^2 -1} dx $$

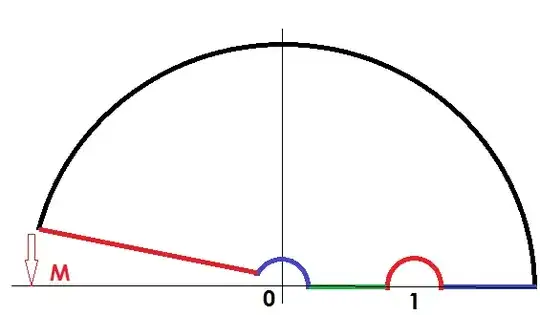
The branch cut of the $log(x)$ is excluded by rotating the red line by an infinitesimal angle M. The origin and the pole on the real axis are both excluded by going around them. I have denoted the semicircle around the origin with $S_{\epsilon}$ and the other semicircle around the pole at 1 with $S_\delta$. The large semicircle is $S_R$. $\epsilon$, $\delta$ and $R$ are the corresponding radii. On the described contour $\Gamma$ the integral should vanish. The integral is

$$ \int_\Gamma {log(x) \over x^2 -1} dx = \int_R^\epsilon {log(re^{i\pi})e^{i\pi} \over r^2 -1} dr + \int_\pi^0 {log(\epsilon e^{i\phi})\epsilon e^{i\phi} \over (\epsilon e^{i\phi})^2 -1} d\phi + \int_\epsilon^{1-\delta} {log(r) \over r^2 -1} dr + \int_\pi^0 {log(\delta e^{i\phi})\delta e^{i\phi} \over (\delta e^{i\phi})^2 -1} d\phi + \int_{1+\delta}^R {log(r) \over r^2 -1} dr + \int_\epsilon^{1-\delta} {log(r) \over r^2 -1} dr + \int_0^\pi {log(R e^{i\phi})R e^{i\phi} \over (R e^{i\phi})^2 -1} d\phi = 0 $$

Taking the limits $R \to \infty$, $\delta \to 0$ and $\epsilon \to 0$, the integrals over the semicircles $S_{\epsilon}$ , $S_\delta$ and $S_R$ vanish. Therefore we are left with:

$$ \int_0^\infty {log(r)+i\pi \over r^2-1}dr + \int_0^\infty {log(r) \over r^2-1}dr=2\int_0^\infty {log(r) \over r^2-1}dr+\int_0^\infty {i\pi \over r^2-1}dr = 0 $$

The last integral is divergent (Mathematica), however, again according to Mathematica the answer to my question is $\pi^2 \over 4$. I have tried to calculate the last integral by using the same contour as before without the indent contour $S_\epsilon$ around zero and including only the pole at $r=1$ with factor $\frac12$. This second contour I have denoted by $\gamma$. If I had tried to go a full half circle, I would have had both poles at $r=1$ and $r=-1$ included and the residue theorem would have given me zero. Therefore I have excluded one of them by the wedge and obtained $$ \int_\gamma {i\pi \over r^2-1}dr = \int_R^0 {i\pi e^{i\pi} \over r^2-1}dr + \int_0^R {i\pi \over r^2-1}dr = 2 \int_0^\infty {i\pi \over r^2-1}dr =i \pi Res({i\pi \over r^2-1},r=1) $$ Evaluating the residue I have obtained precisely $-{\pi^2 \over 2}$. Is this selection of contour allowed? Dropping one pole and keeping the other? Is the selection of the integration contour that arbitrary? I always have such moments doubt. This is why I would appreciate any ideas or comments.

Thanks, Alex

Answer 1

Unfortunately, the divergent integral is part of the integration process. Fortunately, it all works out. Personally, I do not like semicircular contours with logs, although sometimes they do work out. I prefer using keyhole contours on modified integrands. Thus, consider the integral

$$\oint_C dz \frac{\log^2{z}}{z^2-1}$$

where $C$ is a keyhole contour about the positive real axis (where I am taking the branch cut), modified with semicircular divots above and below the real axis at $z=1$. Because the singularity at $z=1$ is removed, the integrals about those divots will vanish. Also, as you point out, the integrals about the circular contours about the origin, both small and large, also vanish as radii go to $0$ and $\infty$, respectively. Thus we have

$$\int_0^{1-\epsilon} dx \frac{\log^2{x}}{x^2-1} + i \epsilon \int_{\pi}^{0} d\phi \, e^{i \phi} \frac{\log^2{(1+\epsilon e^{i \phi})}}{(1+\epsilon e^{i \phi})^2-1}+\\ \int_{1+\epsilon}^{\infty} dx \frac{\log^2{x}}{x^2-1} + \int^{\infty}_{1+\epsilon} dx \frac{(\log{x}+i 2 \pi)^2}{x^2-1}+\\ i\epsilon \int_{2 \pi}^{\pi} d\phi \, e^{i \phi} \frac{[\log{(1+\epsilon e^{i \phi})}+i 2 \pi]^2}{(1+\epsilon e^{i \phi})^2-1}+ \int_{1+\epsilon}^{\infty} dx \frac{(\log{x}+i 2 \pi)^2}{x^2-1}$$

being equal to $i 2 \pi$ times the residue of the integrand at the pole $z=-1$. Thus, with a little algebra, we have

$$-i 4 \pi \int_0^{\infty} dx \frac{\log{x}}{x^2-1} + 4 \pi^2 PV \int_0^{\infty} dx \frac{1}{x^2-1} - 4 \pi^2 i\epsilon \int_{2 \pi}^{\pi} d\phi \, e^{i \phi} \frac{1}{(1+\epsilon e^{i \phi})^2-1} = i 2 \pi \frac{(i \pi)^2}{2 (-1)}$$

Now the last two terms on the RHS are equal to

$$4 \pi^2 \lim_{\epsilon \to 0} \left [\int_0^{1-\epsilon} dx \frac{1}{x^2-1}+ \int_{1+\epsilon}^{\infty} dx \frac{1}{x^2-1}\right ] -i 4 \pi^2 \lim_{\epsilon \to 0} \, \epsilon \int_{2 \pi}^{\pi} d\phi \, e^{i \phi} \frac{1}{(1+\epsilon e^{i \phi})^2-1} $$

For the integrals in the bracket, you can see they sum to zero by substituting $x=1/u$ in the second integral:

$$\int_{1+\epsilon}^{\infty} dx \frac{1}{x^2-1} = \int_{1/(1+\epsilon)}^{\infty} \frac{du}{u^2} \frac{1}{(1/u^2)-1} =\int_0^{1-\epsilon} du \frac{1}{1-u^2} $$

Thus we have

$$-i 4 \pi \int_0^{\infty} dx \frac{\log{x}}{x^2-1} - 4 \pi^2 \left ( -i \frac{\pi}{2}\right) = i \pi^3$$

or

$$\int_0^{\infty} dx \frac{\log{x}}{x^2-1} = \frac{\pi^2}{4}$$

Note that I did not invoke residues technically, although it did work out that way. Rather, I got the result from a careful treatment of the integration contour in the face of a seemingly-divergent integral which is really just a badly expressed contour integral.

ADDENDUM

The integral may be evaluated using real techniques as well. You should be able to show, by splitting the integration interval into $[0,1]$ and $[1,\infty]$ and using a substitution trick similar to the one I used above in showing that the Cauchy PV is zero, to show that

$$\int_0^{\infty} dx \frac{\log{x}}{x^2-1} = -2 \int_0^1 dx \frac{\log{x}}{1-x^2}$$

Now Taylor expand the denominator of the integrand to get

$$-2 \sum_{k=0}^{\infty} \int_0^1 dx \, x^{2 k} \, \log{x}$$

Use the fact that

$$\int_0^1 dx \, x^{2 k} \, \log{x} = -\frac{1}{(2 k+1)^2}$$

and get

$$\int_0^{\infty} dx \frac{\log{x}}{x^2-1} = 2 \sum_{k=0}^{\infty} \frac{1}{(2 k+1)^2} = \frac{\pi^2}{4}$$

Answer 2

I have finally figured out how to solve the integral in a very simple way. Take a keyhole contour as suggested by Ron Gordon. It is easy to see that the contributions from the divots round 1 are zero. This is due to the fact that the integrand function $ {log(z) \over z^2 - 1} $, i.e. the $log(z)$ is analytic near 1, and the integrand can be expressed as $$ {log(z) \over z^2 - 1} = {a_{-1} \over z – 1} +\phi(z) $$ Where $\phi(z)$ is an analytic function in the neighborhood of 1. Now since $\phi(z)$ is analytic and therefore bounded, the integral of it along the divots I zero. The remaining part also vanishes. The trick is to use $log^2(z)$. So what we get is $$ (\int_{\epsilon}^{1-\epsilon} + \int_{1+\epsilon}^R) {(log(r)+2 i \pi)^2 \over z^2 -1 } -(\int_{\epsilon}^{1-\epsilon} + \int_{1+\epsilon}^R) {log^2(r) \over z^2 -1 } = {2 i \pi (i\pi)^2 \over -2} $$ This is equal to: $$ -4 i \pi \int_0^{\infty} + V.P. \int_0^{\infty} {4\pi^2 \over z^2 – 1} = {2 i \pi (i\pi)^2 \over -2} $$

Equating the real and the imaginary parts we get the results. Note that the $V.P.$ is automatically equal to zero.

Thanks for the help.