$\newcommand{\angles}[1]{\left\langle\, #1 \,\right\rangle}
\newcommand{\braces}[1]{\left\lbrace\, #1 \,\right\rbrace}
\newcommand{\bracks}[1]{\left\lbrack\, #1 \,\right\rbrack}
\newcommand{\ceil}[1]{\,\left\lceil\, #1 \,\right\rceil\,}
\newcommand{\dd}{{\rm d}}
\newcommand{\ds}[1]{\displaystyle{#1}}
\newcommand{\expo}[1]{\,{\rm e}^{#1}\,}
\newcommand{\fermi}{\,{\rm f}}
\newcommand{\floor}[1]{\,\left\lfloor #1 \right\rfloor\,}
\newcommand{\half}{{1 \over 2}}
\newcommand{\ic}{{\rm i}}
\newcommand{\iff}{\Longleftrightarrow}
\newcommand{\imp}{\Longrightarrow}
\newcommand{\pars}[1]{\left(\, #1 \,\right)}
\newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}}
\newcommand{\pp}{{\cal P}}
\newcommand{\root}[2][]{\,\sqrt[#1]{\vphantom{\large A}\,#2\,}\,}
\newcommand{\sech}{\,{\rm sech}}
\newcommand{\sgn}{\,{\rm sgn}}
\newcommand{\totald}[3][]{\frac{{\rm d}^{#1} #2}{{\rm d} #3^{#1}}}
\newcommand{\ul}[1]{\underline{#1}}
\newcommand{\verts}[1]{\left\vert\, #1 \,\right\vert}$
$\ds{I\equiv\int_{0}^{\infty}{\ln\pars{x} \over \pars{x - 1}\root{x}}\,\dd x:
\ {\large ?}}$.
\begin{align}
I&\equiv\
\overbrace{\int_{0}^{\infty}{\ln\pars{x} \over \pars{x - 1}\root{x}}\,\dd x}
^{\ds{\color{#c00000}{x\ \mapsto\ x^{2}}}}\ =\
\int_{0}^{\infty}{\ln\pars{x^{2}} \over \pars{x^{2} - 1}x}\,2x\,\dd x
=-4\int_{0}^{\infty}{\ln\pars{x} \over 1 - x^{2}}\,\dd x
\\[5mm]&=-4\int_{0}^{1}{\ln\pars{x} \over 1 - x^{2}}\,\dd x
-4\int_{1}^{0}{\ln\pars{1/x} \over 1 - x^{-2}}\,\pars{-\,{\dd x \over x^{2}}}
=-8\int_{0}^{1}{\ln\pars{x} \over 1 - x^{2}}\,\dd x
\\[5mm]&=-4\ \overbrace{\int_{0}^{1}{\ln\pars{x} \over 1 - x}\,\dd x}
^{\ds{\color{#c00000}{x\ \mapsto\ 1 - x}}}\ -\
4\ \overbrace{\int_{0}^{1}{\ln\pars{x} \over 1 + x}\,\dd x}
^{\ds{\color{#c00000}{x\ \mapsto\ -x}}}\ =\
-4\int_{0}^{1}{\ln\pars{1 - x} \over x}\,\dd x
+4\int_{0}^{-1}{\ln\pars{-x} \over 1 - x}\,\dd x
\\[5mm]&=-4\int_{0}^{1}{\ln\pars{1 - x} \over x}\,\dd x
+4\braces{\overbrace{\left.\vphantom{\LARGE A}%
-\ln\pars{1 - x}\ln\pars{-x}\right\vert_{0}^{-1}}^{\ds{=\ \color{#c00000}{0}}}\ +\
\int_{0}^{-1}{\ln\pars{1 - x} \over x}\,\dd x}
\\[5mm]&=4\int_{-1}^{1}\bracks{-\,{\ln\pars{1 - x} \over x}}\,\dd x
=4\int_{-1}^{1}{\rm Li}_{2}'\pars{x}\,\dd x
=4\bracks{%
\underbrace{{\rm Li}_{2}\pars{1}}_{\ds{\color{#c00000}{\pi^{2} \over 6}}}\ -\
\underbrace{{\rm Li}_{2}\pars{-1}}_{\ds{\color{#c00000}{-\,{\pi^{2} \over 12}}}}}
=4\pars{\pi^{2} \over 4}
\\[5mm]&=\color{#66f}{\Large \pi^{2}}
\end{align}
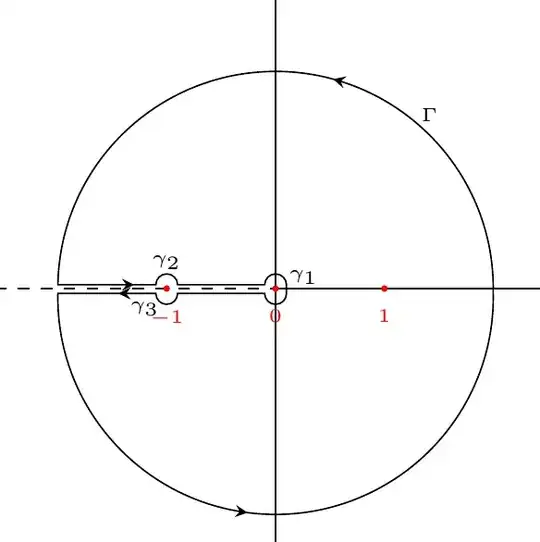
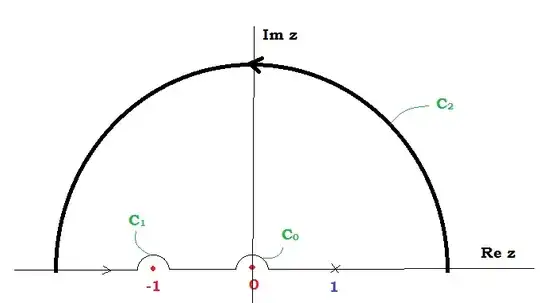
Furthermore, where exactly is your branch cut located?
– tired Nov 19 '14 at 21:24