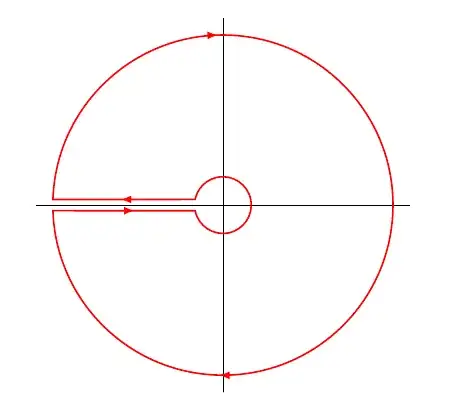
I am asked to show that
$$\displaystyle \int_{0}^{\infty} \frac{\ln(x)}{(x^2-1)} = \frac{\pi^2}{4}.$$
So I think I'm supposed to use residues to solve this integral and integrate around a contour on the real line. The thing is that I don't know how to choose this contour since the poles will lie on the path and I would also have to bent around zero since $\ln(x)$ has a non essential singularity there. I tried to do this with the methods that I've learned but I got as an answer $-\pi^2$ which is wrong. Any help on how to proceed is appreciated.