Contour integration $ \int_0^\infty \frac{\log x}{1-x^{8}}\,dx\, $

Question

I am tasked to compute the integral

$$ \int_0^\infty \frac{\log(x)}{1-x^{8}}\,dx\, $$

using contour integration. I've seen some approaches to complex logarithms, but never with such a function in the denominator.

I can't seem to figure out which contour fits this problem best. If I choose a semicircle in the upper right quadrant I can avoid the singularity at the origin, but I still can't deal with the singularity at $z = i$ (or the integral along that line, in fact).

I'd really appreciate some help here.

This contour and setup may work https://math.stackexchange.com/a/1613373/254075. — sharding4, Jun 19 '17 at 00:53
Good first question! Don't forget about how $log$ behaves near $0$, and the choice of branch cut. — B. Mehta, Jun 19 '17 at 00:54

Simply Beautiful Art · Answer 1 · 2017-06-19T01:55:03.233

8

Hint:

Consider the following contour with $\Gamma=\Gamma_1\cup\Gamma_2\cup\Gamma_3$ and an angle of $\pi/8$.

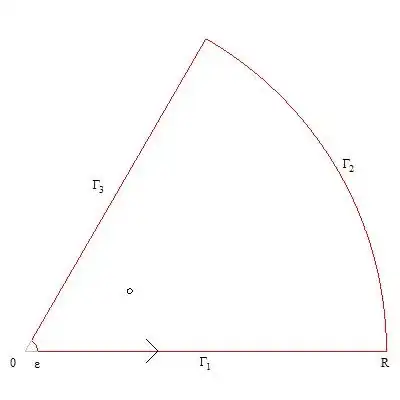
It is trivial to show that

$$\lim_{R\to\infty}\int_{\Gamma_2}\frac{\ln(z)}{1-z^8}~\mathrm dz=0$$

$$\lim_{(e,R)\to(0^+,\infty)}\int_{\Gamma_1}\frac{\ln(z)}{1-z^8}~\mathrm dz=\int_0^\infty\frac{\ln(z)}{1-z^8}~\mathrm dz$$

$$\lim_{(e,R)\to(0^+,\infty)}\int_{\Gamma_3}\frac{\ln(z)}{1-z^8}~\mathrm dz=-e^{\pi i/8}\int_0^\infty\frac{\ln(z)+\frac\pi8}{1+z^8}~\mathrm dz$$

and the indent likewise tends to zero. Thus, we have

$$\int_0^\infty\frac{\ln(z)}{1-z^8}~\mathrm dz=e^{\pi i/8}\int_0^\infty\frac{\ln(z)+\frac\pi8}{1+z^8}~\mathrm dz+\oint_\Gamma\frac{\ln(z)}{1-z^8}~\mathrm dz$$

The right integral may then be dealt with using the residue theorem.

Now consider $f(z)=\frac{[\ln(z)]^2}{1+z^8}$ and the keyhole contour with $C=C_1\cup C_2\cup C_3\cup C_4$ and $r,R$ being the inner radius and outer radius respectively.

We then have:

$$\lim_{(r,R)\to(0^+,\infty)}\int_{C_2}f(z)~\mathrm dz=\lim_{(r,R)\to(0^+,\infty)}\int_{C_4}f(z)~\mathrm dz=0$$

$$\lim_{(r,R)\to(0^+,\infty)}\int_{C_1}f(z)~\mathrm dz=\int_0^\infty\frac{[\ln(z)]^2}{1+z^8}~\mathrm dz$$

$$\lim_{(r,R)\to(0^+,\infty)}\int_{C_3}f(z)~\mathrm dz=-\int_0^\infty\frac{[\ln(z)+2\pi i]^2}{1+z^8}~\mathrm dz$$

Adding these together, we find that

$$\begin{align}\lim_{(r,R)\to(0^+,\infty)}\oint_Cf(z)~\mathrm dz&=\int_0^\infty\frac{[\ln(z)]^2-[\ln(z)+2\pi i]^2}{1+z^8}~\mathrm dz\\&=\int_0^\infty\frac{-4\pi i\ln(z)+4\pi^2}{1+z^8}~\mathrm dz\end{align}$$

Thus,

$$\int_0^\infty\frac{\ln(z)}{1+z^8}~\mathrm dz=-\frac1{4\pi}\Im\left[\lim_{(r,R)\to(0^+,\infty)}\oint_Cf(z)~\mathrm dz\right]$$

$$\int_0^\infty\frac1{1+z^8}~\mathrm dz=\frac1{4\pi^2}\Re\left[\lim_{(r,R)\to(0^+,\infty)}\oint_Cf(z)~\mathrm dz\right]$$

Now apply residue theorem and you are done!

edited Jun 19 '17 at 01:55

answered Jun 19 '17 at 00:57

Simply Beautiful Art

74,685

There's no square on the log in the original question? – Robert Israel Jun 19 '17 at 01:00
@RobertIsrael Corrected the last line. The idea is that the squared parts cancel... – Simply Beautiful Art Jun 19 '17 at 01:01
@RobertIsrael standard trick to handle log above and below the branch cut – sharding4 Jun 19 '17 at 01:02
Seems like there is a problem with $\int_0^\infty\frac{-4\pi i\ln(z)+4\pi^2}{1-z^8}~\mathrm dz$ though. $\int_0^\infty\frac{4\pi^2}{1-z^8}~\mathrm dz$ ins't convergent, is it? – sharding4 Jun 19 '17 at 01:04
@sharding4 Ah, that is an interesting problem... – Simply Beautiful Art Jun 19 '17 at 01:16
@sharding4 Think it can be handled as the principal value of that integral? – Simply Beautiful Art Jun 19 '17 at 01:22
No. Don't think so. Would be a handy spot for "renormalization." – sharding4 Jun 19 '17 at 01:24
They do $\int_0^\infty\frac{\log x, dx}{x^2-1}$ here -> https://math.stackexchange.com/q/293990/254075 using an "indented quarter circle" contour – sharding4 Jun 19 '17 at 01:29
Ugh. that last suggestion won't work because of eighth roots of unity like $i$ on the contour. – sharding4 Jun 19 '17 at 01:32
@sharding4 Indeed, I was just pondering the use of an arc with angle $\pi/\alpha$... – Simply Beautiful Art Jun 19 '17 at 01:32
@sharding4 :D I think I've done it right this time. – Simply Beautiful Art Jun 19 '17 at 01:45
I think so. I wondered whether the $1+z^8$ would have to pop out in the calculation. – sharding4 Jun 19 '17 at 01:52
I'm very thankful to both of you sharding4 and SBA for your hard work. This integral was on one of our exam tests and I'm very surprised by the approach required to evaluate it. Thank you – Agony Jun 19 '17 at 09:48

score 3 · Answer 2 · answered Jun 19 '17 at 04:17

We can also evaluate the integral by substituting $x^8 = t$, the integral then becomes:

$$-\frac{1}{64}\int_0^{\infty}\frac{t^{-\frac{7}{8}}\log(t) dt}{t-1}$$

We can evaluate this integral using the result:

$$\int_0^{\infty}\frac{x^{-p}dx}{1+x} = \frac{\pi}{\sin(\pi p)}\tag{1}$$

This is easy to prove using contour integration of $\dfrac{z^{-p}}{1+z}$ along the keyhole contour given in Simply Beautiful Art's answer. It follows from Eq. (1) that:

$$\int_0^{\infty}\frac{x^{-p}dx}{a+x} = \frac{\pi a^{-p}}{\sin(\pi p)}$$

for positive real $a$. Taking minus the derivative w.r.t. $p$ yields:

$$\int_0^{\infty}\frac{x^{-p}\log(x)dx}{a+x} = \frac{\pi a^{-p}\log(a)}{\sin(\pi p)} + \frac{\pi^2 a^{-p}\cos(\pi p)}{\sin^2(\pi p)} \tag{2}$$

To compute the desired integral, we need to put $a = -1$, but the above result has been obtained for real positive $a$. We can deal with this problem by analytically continuing the result, the integral is a analytic function in a cut-plane where we have a branch point at the origin. The branch cut can be chosen in an arbitrary way, but for negative real $a$ it matters how you choose the branch cut, unless $a = -1$.

If we put the branch cut on the negative imaginary axis, then an analytic continuation of $a$ from the positive real axis to the negative real axis can be written as an integral that avoids the singularity at $x = -a$ by deforming the contour there a bit into the positive imaginary direction. The original integral with positive $a$ could have been deformed that way, and if we then move $a$ along a path in the upper half plane into the indentation of the contour, the integral changes in an analytic way. The interpretation of the result is then that it yields the principal part of the integral minus $\pi i$ times the residue at $x = -a$.

If we put the branch cut along a path in the upper half plane, then analytically continuing $a$ to negative real values, amounts to pushing the singularity at $z = -a$ from above onto the contour, so the contour is then going to be deformed into the negative half plane. This means that the result can be interpreted as the principal value of the integral plus $\pi i$ times the residue at $x = -a$.

But since we're considering the case $a = -1$ where the integrand only has a removable singularity at $x = 1$, the analytic continuation is the integral from zero to infinity for both choices of the branch cut. We can directly verify this by inserting $a = \exp(\pm i\pi)$ in Eq. (2), as expected this yields a result that is independent of the sign in the exponential, the result is then:

$$\int_0^{\infty}\frac{x^{-p}\log(x)dx}{x -1} =\frac{\pi^2}{\sin^2(\pi p)}$$

Using this result we see that the original integral evaluates to:

$$-\frac{\pi^2}{16}\left(1+\frac{\sqrt{2}}{2}\right)$$

Contour integration $ \int_0^\infty \frac{\log x}{1-x^{8}}\,dx\, $

2 Answers2

Hint: