Euler’s formula states that $e^{i x} = \cos(x) + i \sin(x)$.
I can see from the MacLaurin Expansion that this is indeed true; however, I don’t intuitively understand how raising $e$ to the power of $ix$ produces rotation. Can anyone give me an intuitive understanding?
Starting with this formulation of $e^x$ $$ e^x=\lim_{n\to\infty}\left(1+\frac xn\right)^n\tag{1} $$ and extending this definition to $e^{ix}$: $$ e^{ix}=\lim_{n\to\infty}\left(1+\frac{ix}{n}\right)^n\tag{2} $$ For a complex number $z$, let $|z|$ be its magnitude and $\arg(z)$ be its angle. If it is not already known, only a small amount of algebra and trigonometry is needed to show that $$ \begin{align} |wz|&=|w|\cdot|z|\tag{3a}\\ \arg(wz)&=\arg(w)+\arg(z)\tag{3b} \end{align} $$ Induction then shows that \begin{align} |z^n|&=|z|^n\tag{4a}\\ \arg(z^n)&=n\arg(z)\tag{4b} \end{align} Let us take a closer look at $1+\dfrac{ix}{n}$. $$ \begin{align} \left|\,1+\frac{ix}{n}\,\right|&=\sqrt{1+\frac{x^2}{n^2}}\tag{5a}\\ \tan\left(\arg\left(1+\frac{ix}{n}\right)\right)&=\frac xn\tag{5b} \end{align} $$ Using $(4a)$, $(5a)$, and $(2)$, we get $$ \begin{align} |e^{ix}| &=\lim_{n\to\infty}\left|\,1+\frac{ix}{n}\,\right|^n\\ &=\lim_{n\to\infty}\left(1+\frac{x^2}{n^2}\right)^{n/2}\\ &=\lim_{n\to\infty}\left(1+\frac{x^2}{n^2}\right)^{\frac{n^2}{2n}}\\ &=\lim_{n\to\infty}e^{\frac{x^2}{2n}}\\[12pt] &=1\tag{6} \end{align} $$ It can be shown that when $x$ is measured in radians $$ \lim_{x\to0}\frac{\tan(x)}{x}=1\tag{7} $$ Using $(4b)$, $(5b)$, and $(7)$, we get $$ \begin{align} \arg(e^{ix}) &=\lim_{n\to\infty}n\arg\left(1+\frac{ix}{n}\right)\\ &=\lim_{n\to\infty}n\arg\left(1+\frac{ix}{n}\right) \frac{\tan\left(\arg\left(1+\frac{ix}{n}\right)\right)}{\arg\left(1+\frac{ix} {n}\right)}\\ &=\lim_{n\to\infty}n\frac xn\\ &=x\tag{8} \end{align} $$ Using $(6)$ and $(8)$, we get that $e^{ix}$ has magnitude $1$ and angle $x$. Thus, converting from polar coordinates: $$ e^{ix} = \cos(x) + i\sin(x)\tag{9} $$ We get the rotational action from $(9)$ and $(3)$.
Consider a particle moving along the path $f(t)=e^{i t}$. It's instantaneous velocity is given by the derivative, and convince yourself that it is, treating $i$ as a constant, $ie^{it}$ Thus we see
$$\text{Velocity} = i\text{Position} = \text{Position (rotated by} \frac{\pi}{2} \text{radians)}$$
Because $f(0) = 1$, intitial velocity is $i$. Moving the position slightly and changing the velocity shows us that $|f(t)| = 1$ and thus $|\frac{d}{dt}f(t)|=1$. If $t =\theta$, the particle will have traveled $\theta$ radians around the unit circle.
Let's look at the $|e^{ix}|$, this is always constant $ (|\cos x + i \sin x| = \sqrt{ \cos^2x + \sin^2x} = 1)$. The only thing that is changed is $x$, now if we assign coordinates to real $(\cos x$) as $x$-coordinate and complex value $(\sin x)$ as $y$-coordinate (or imaginary axis), then this is same as parametric equation of unit circle with $x$ as parameter. As $x$ increases, the path traced by the point will be circular.
I don't know exactly what kind of intuition you're looking for. You're probably thinking about $e^{i\theta}$ the same way you would $2^2$; that is, $e^{i\theta}$ is found by multiplying $e$ by itself $i\theta$ times. While this is useful for introducing exponentiation of the form $n^m$ when $n,m$ are positive integers, it doesn't really make sense to try and apply this kind of reasoning to expressions of the form $a^x$ or $a^z$ for real or complex arguments.
The only sort of intuition I can suggest is the following: what is $e$? It's typically defined by the expression $\sum_{n=0}^{\infty} \frac{1}{n!}$. This isn't an alternate interesting fact but a definition for the number $e$. We also define $e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!}$, and we observe that this series converges for all real $x$. This is just what the expression $e^x$ means. Similarly, $e^{i \theta}$ is defined by $\sum_{n=0}^{\infty} \frac{(i \theta)^n}{n!}$, and it just so happens that this converges absolutely for all $z$, giving us Euler's formula.
This is why $e^{i\theta}$ is a rotation about the unit circle in $\mathbb{C}$. Because it's defined that way.
$\exp(z)$ is the function which is its own derivative. It's natural to introduce coordinates since we're thinking about the circle (a 2D figure).
We can consider it's real and imaginary parts: $\exp(iy) = c(y) + is(y)$, differentiating gives $\exp(iy) = - i c'(y) + s'(y)$ comparing with the previous gives $s'(y) = c(y)$ and $c'(y) = - s(y)$.
From the power series we find the real part is all the even powers so $c(-y) = c(y)$ and the imaginary part is all the odd powers so $s(-y) = -s(y)$, this lets us conclude Pythagoras' theorem $c(y)^2 + s(y)^2 = \exp(iy)\exp(-iy) = 1$.
From that we easily deduce that the path $(c(y),s(y))$ lies on the unit circle and is arc-length parametrized. Therefore it returns to its starting point when $y$ reaches $2 \pi$.
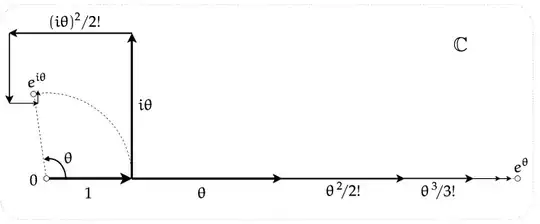
No rotation is involved. The equality is simply describing the location of a point on the complex circle. Motion implies time. There is no motion without time. Motion is change in the time dimension. Therefore, motion of a point in the complex plane is, in itself, a 3 dimensional graph. We can involve time by changing the equation to $e^{i\Theta} = \cos(t)+i\sin(t)$. This gives 3 dimensions, time and the complex circle. A perfect example is a point moving on a circle on an oscilloscope when the horizontal and vertical deflection voltages are $V_h=V\cos(t), V_v=V\sin(t)$. Deflection of the electron beam is proportional to voltage. $e^{i\theta}=e^{it}$. This easy substitution just begs to be motion before changing $\theta$ to $t$.
We could change the graph to another form by converting time to another dimension. Call it the ''$z$'' dimension, where $z=t$. This is done to put $t$ into a spatial form, "freezing" it. The graph becomes the continuous function $z=e^{it}+t$, where t (or substitute $x$ or $\theta$) is a real number. Notice that variables $t,x$ are both describing static loci, as the function is not in motion. Yes, it is an unusual function as the locus is a circle plus a component along the $z$ axis. All said, it is a 3 dimensional graph. It is a helix in the perpendicular $z$ direction.
"Freezing" time and changing dimensions is commonly done. Throw a ball straight up into the air (the $y$ direction). Visualize the motion. Now, convert the time dimension to the orthogonal $x$ dimension. Graphing results in a parabola in the $(x,y)$ plane, where $t=x$.
It is worth repeating that moving the point on the helix or throwing the ball sideways (the trajectory of a ball thrown laterally is a parabola) is so compelling due to the easy substitutions. Remember, $t$ is frozen. Any additional motion would be yet another dimension from the converted graphs, which are geometric entities in their own right. Consider $f(x)=x$. Most people would consider this a static function. Few people would be compelled to have a point moving along the line. A point used as a cursor would be just fine. But formalizing this motion would result in going into another dimension. Resist temptation. But if you have a quarter and must...
Treat yourself and go to a spiral gumball machine to watch a 4 dimensional gumball. It is also the graph of $f(z)=re^\frac{ia_rt^2}{2}+\frac{ka_rt^2}{2}$, where $z$ is a complex number. The solution is wherever the ball is at a given time.
$$z'=\frac{ka_rt^2}{2}$$$$t'=re^{\frac{ia_rt^2}{2}}$$$$f(z)=z'+t'$$
The primed numbers are used to differentiate coordinates from other numbers
r is the radius of the gumball drop
$a_r$ is the acceleration of the ball down the slope, different for different helices
k is a proportionality constant related to the pitch
For constant a, $d=\frac{at^2}{2}$ or $s=\frac{at^2}{2}$ for circular units
In general, consider the complex plane to be the initial location of the gumball for any size gumball machine with helices on the same helicoid ("filled in" helix or a screw).
The big picture is the important thing. Every point on the complex plane $(r,\theta)$ is mapped by a function $f(z)$ to 2 new variables $(z',t')$.
I visualize this as a rotating plane accelerating on the $z'$-axis changing shape as the inner radii accelerate faster.
Going back to the beginning, modify Euler's formula to: $$e^{if(\theta)}=\cos(f(\theta))+ i\sin(f(\theta))$$
The questioner's implicit choice is $t=f(\theta)$. Euler's formula is $\theta=f(\theta)$. Consider $f(x)=x$. Add $z'$. Call it a trivial change. $f(x)=x$ is so fundamental it doesn't even need 2 dimensions. It can be described by the real number line as $x=x$. When $t$ represents time, $t=f(\theta)$ puts the function in motion, creating another dimension $t'$. The case of $t=f(\theta)$ could be considered the trivial case in $t'$, as $z'=f(x)=x$ is in $z'$. A dimension is added, but the variables don't change. $f(\theta)=a_rt^2/2$ is what sends the gumball into the 4th dimension as a complex function. The graph of $e^{i\theta}$ is "smeared" by multiple values of the phasor representing it's location. In most cases, this is resolved by creating a $z'=t'$ dimension, as noted earlier, to graph the function. In the gumball's case, the $z'$ dimension is already taken up by the necessity of the gumball to stay in the fixed loci of the helix. The only choice is to go into the time range to graph the function uniquely. Velocity, in a circle, IS ORTHOGANAL to that circle, confirming motion is in a new dimension.
$e^{it}$ is more than position.
It is the time dimension.
PART 2
THE 4 DIMENSIONAL PARABOLA, $W=Z^2$
$x^2-y^2=z$ is a hyperbolic paraboloid, where $x,y,z$ are real numbers. It is a beautiful saddle shaped 3 dimensional quadric. It is the usual end of the road for students of complex numbers in that it shows where the hidden (imaginary) roots of $y=x^2$ are. It is formed by rotating the real part of $y=x^2$, a parabola, 90° into the complex $(z)$ plane, then flipping it (reflection in the complex plane). This is the skeleton of the function: 2 parabolas intersecting at their vertices, rotated 90° from each other. One parabola's vertex then moves along the other's locus, the resulting parabolas parallel to the one before it. They do this mutually, so it doesn't matter which one moves. It creates the same geometric figure. Unknown to some, this hyperbolic paraboloid only gives the real values of a more general squaring function $f(z)=f(x+yi)^2$, where $z$ is a complex number. In the following, I use "$a$" as the real value of the function. Therefore, $a=x^2$. $a$ could be described as "altitude".
Map $(x,y)$ to $(a,t)$, where $z=x+yi, w=a+ti, x,y,a,t$ are real numbers, $w$ and $z$ are complex. $$w=z^2=(x+yi)^2=x^2-y^2+2xyi$$ $$=a+ti$$ $$=Re+Im$$ The real part: $x^2-y^2=a$ is the equation of our hyperbolic paraboloid. Not always done, the following is a 2 function derivation which illustrates it's construction very well. $$a=f(x)=x^2$$ let $$u=x^2, v=(yi)^2$$ $$Re=u+v=x^2-y^2$$ At any point along our 2-dimensional parabola, $u$, add the imaginary component, $v$, in an orthogonal direction (or add the real parabola to the imaginary).
The imaginary part: $2xy=a$ is the equation of a hyperbolic paraboloid. It is rotated $\pi/4$ (45°) CCW in the complex plane ($z$ plane) from the $x^2-y^2=a$ hyperbolic paraboloid. The problem is, it is an imaginary hyperbolic paraboloid and $a$ is real. How do we graph it? The $a$ dimension is already taken. As is always done, a 2 function derivation is performed on $w$. $$w=Re+Im$$ $$ =a+ti$$ let $$u=x^2-y^2, v=2xy$$ $$w=u+vi$$ These 2 functions are then transformed, rotated, or changed in some way to a $w$ plane, often with the $w$ plane being coincident with the $z$ plane (a rotation).
What is needed is a 2 dimensional solution to $w$ instead of a strictly 2 function solution. We already have the dimension $a$. We're halfway there. All we need is one more orthogonal dimension. Remember, changing time to another dimension is commonly done. Now, we are going to change a space dimension into a time dimension. We know $a=2xy$. Let $t=2xy$. This "collapses" the $a$ dimension and places the range strictly in the $z$ plane. It is still a hyperbolic paraboloid. It still has 3 dimensions. But it "unfreezes" time. The graph becomes a hyperbola approaching the origin in the 2nd and 4th quadrants, instantly becoming 2 perpendicular lines (which coincide with the $x,y$ axes), then moving away from the origin in the 1st and 3rd quadrants. Call this the time hyperbolic paraboloid, designate $hp_t$.
The mapping of the 4 dimensional parabola is the sum of the original hyperbolic paraboloid, the "space hyperbolic paraboloid", $hp_s$, and $ hp_t$. As in any graph of any complex number, it is determined by the intersection of a real number and an imaginary number. So, at time $2xy$, the time hyperbola will project a 3 dimensional algebraic line onto $hp_s$ (the intersection of a hyperbolic right cylinder, at a particular instant, onto $hp_s$). The result is a line (of intersection) moving towards or away (depending on the sign of $2xy$) the origin from or to infinity. This line is a skewed hyperbola. At the origin, the skewed hyperbola becomes the skeletal space parabolas (defined shortly).
I like to call $a=x^2$ and $a=(iy)^2$ the skeletal space parabolas. The vertices of the $hp_s$ hyperbolas follow the loci of these parabolas. The vertices of the $hp_t$ hyperbolas similarly follow the skeletal time parabolas $t=R^2$ and $t=i(iR)^2$, where $R$ is real and lies along the $x=y$ axis. This is easier to see when $hp_t$ is in the "$a$" range. In the "$t$" range this still occurs, but the time parabolas are coincident with the real degenerate hyperbola.
In polar coordinates: $z=re^{i\theta}=x+yi$ where $r,\theta$ are real $$f(z)=f(re^{i\theta})=z^2=r^2e^{i2\theta}=(x^2-y^2)+2xyi$$ $x^2-y^2=r^2\cos^2(\theta)-r^2\sin^2(\theta)=r^2(\cos^2(\theta)-\sin^2(\theta))=r^2\cos(2\theta)$ by double angle identity. $2xy=2r\cos(\theta) r\sin(\theta) =2r^2\sin(\theta) \cos(\theta)=r^2\sin(2\theta)$ by double angle identity $$z^2=r^2\cos(2\theta)+ir^2\sin(2\theta)$$ In Euler's formula:$$e^{if(\theta)}=\cos(f(\theta))+i\sin(f(\theta))$$ when$$f(z)=z^2, f(\theta)=\arg(\theta)=2\theta$$ $$t=r^2\sin(2\theta)=f(r,\theta)$$ $$a=r^2\cos(2\theta)$$ $t$ is a function of 2 variables as is $a$. In general: $$z=r\cos(\theta)+ir\sin(\theta)$$ $$f(z)=f(r\cos(\theta))+if(r\sin(\theta))$$ where$$a=f(r\cos(\theta)) , t=f(r\sin(\theta))$$THOUGHTS ON THE GRAPH
One might casually note that $z^2$, in it's entire range of $t$, seems to "reconstruct" our traditional h-p. The hyperbolic paraboloid, as we know it, exists statically (doesn't change) in $t$. It is a summation of every instant in time. Call it blocktime or a timescape. Similarly, $hp_t$, in the time range, exists statically in space, appearing as moving cylindrical (spatial value unchanging for each instant in time) hyperbolas. It is the summation of every value in $a$. Hence, the intersection of $hp_t$ and $hp_s$ create $z^2$. The traditional h-p is not a complex function, as a single point $(x,y)$ maps to an infinite number of times $(x,y)→(a,ℝ)$. The difference between $z^2$ and the hyperbolic paraboloid as we know it, is the difference between a cylinder, as we know it, and a circle moving along a helix. The beauty is in the details.
3 dimensions could be defined as a space. As 2 non-parallel surfaces intersect in a curve, 2 non-parallel spaces intersect in a surface. An algebraic line through time is a surface. To map the $z$ plane (a surface) to a function of $z$ (single valued result) , the $w$ plane must be a surface. $hp_t$ and $hp_s$ intersect in that surface.
FLATLANDERS' HOPELESS PROBLEM
Flatlanders (creatures who live in a plane) have a problem. They did their math on $z^2$ and have come up with 2 hyperbolic paraboloids. One has it's axis along the x-axis and the other on an axis rotated $\pi/4$ from the x-axis. Both look like our $hp_t$. They have figured out that complex functions have complex solutions. They find it hard to visualize a solution with all the crisscrossing lines they've created. So, take a moment to reflect on the glory of the geometry that is available to us.
Shitty answers from lame books. The next geometric approach a will appeal to euler's formulas is explored in detail by Needham (1997).
By re-expressing $e^{i \theta}$ as a power series $e^{x} = 1 + x +\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots$, we have:
$$e^{i \theta} = 1 + (i \theta) +\frac{(i \theta)^2}{2!}+\frac{(i \theta)^3}{3!}+\cdots$$
$$e^{i \theta} = 1 + i \theta -\frac{\theta^2}{2!}-\frac{i \theta^3}{3!}+\cdots$$
"This series is just as meaningful as the series for $e^x$, but instead of the terms all having the same direction, here each term makes a right angle with the previous one, producing a kind of spiral." (Needham, 1997)
If we visualize complex numbers as vectors then we are adding these real vectors and imaginary vectors that gets smaller at every term of the power series.
What might not be obvious is that the path it takes as theta changes is actually a circle.
So, we must show two things:
Then, by splitting real and imaginary parts we get:
$$C(\theta)=1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\cdots$$
$$S(\theta)=\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\cdots$$
Thus, $e^{i\theta}=C(\theta)+iS(\theta)$.
Suppose we use the following definition of the exponential function: $$ e^x=\lim_{n\to\infty}\left(1+\frac{x}{n}\right)^n \, . $$ This definition makes sense even when $x$ is a complex number. If $n$ is very large, then $$ 1+\frac{i\theta}{n}\approx\cos\left(\frac{\theta}{n}\right)+i\sin\left(\frac{\theta}{n}\right) $$ using linear approximation. Hence, $$ \left(1+\frac{i\theta}{n}\right)^n\approx\cos\theta+i\sin\theta \, . $$ by de Moivre's theorem. It seems reasonable that in the limit as $n\to\infty$, this approximation turns into exact equality.
