Limits in complex plane.

Question

Let $z$ and $z_n$ be complex numbers and assume $z_n \rightarrow z$. It it true that $$\lim\limits_{n\to \infty}\left(1+\frac{z_n}{n}\right)^n= \lim\limits_{n\to \infty}\left(1+\frac{z}{n}\right)^n ?$$

Note that $\lim\limits_{n\to \infty}\left(1+\frac{z}{n}\right)^n$ exists and I take it as the definition of $e^z$. Further this relation is true (and easy) for real variables.

Note further that if the approach $z_n \rightarrow z$ is non tangential (in otherwords within a Stolz angle) then I have a proof of the above limit equality.

I would like to see either a proof of the general case or a counterexample.

Further what happens if $z_n \rightarrow z$ from outside the radius of $|z|$ ?

Answer 1

Note that we have for $0\leq k\leq n$ $$\frac{\binom{n}{k}}{n^k}=\frac{n(n-1)\cdots(n-k+1)}{k! n^k}\leq \frac{1}{k!}$$

Hence if we put $$\exp(z)-(1+\frac{z}{n})^n=\sum_{k\geq 0} a_{n,k}z^k$$ all the $a_{n,k}$ are $\geq 0$. Let $R>0$, and $z\in \mathbb{C}$, $|z|\leq R$. We have:

$$|\exp(z)-(1+\frac{z}{n})^n|\leq \sum_{k\geq 0} |a_{n,k}||z|^k\leq \sum a_{n,k}R^k=\exp(R)-(1+\frac{R}{n})^n$$ If $z_n\to z$, there exists a $R$ such that $|z|\leq R$ and $|z_n|\leq R$ for all $n$, and hence we get $\displaystyle \exp(z_n)-(1+\frac{z_n}{n})^n\to 0$, and we easily conclude.

Answer 2

Using the methods from this answer, we show the following: $$ \begin{align} \left|\frac{\left(1+\frac{z}n\right)^n}{\left(1+\frac{z+\delta}n\right)^n}\right| &=\left|\,1-\frac\delta{n+z+\delta}\,\right|^n\tag{1a}\\ &\ge\left(1-\frac{|\delta|}{n-|z+\delta|}\right)^n\tag{1b}\\[3pt] &\ge1-\frac{n\,|\delta|}{n-|z+\delta|}\tag{1c} \end{align} $$ Explanation:
$\text{(1a)}$: distribute the exponent over the quotient
$\phantom{\text{(1a): }}$simplify the quotient
$\text{(1b)}$: triangle inequality (twice)
$\text{(1c)}$: Bernoulli's Inequality $$ \begin{align} \left|\frac{\left(1+\frac{z+\delta}n\right)^n}{\left(1+\frac{z}n\right)^n}\right| &=\left|\,1+\frac\delta{n+z}\,\right|^n\tag{2a}\\ &\ge\left(1-\frac{|\delta|}{n-|z|}\right)^n\tag{2b}\\[3pt] &\ge1-\frac{n\,|\delta|}{n-|z|}\tag{2c} \end{align} $$ Explanation:
$\text{(2a)}$: distribute the exponent over the quotient
$\phantom{\text{(2a): }}$simplify the quotient
$\text{(2b)}$: triangle inequality (twice)
$\text{(2c)}$: Bernoulli's Inequality

Therefore, $$ 1-\frac{n\,|\delta|}{n-|z|}\le\left|\frac{\left(1+\frac{z+\delta}n\right)^n}{\left(1+\frac{z}n\right)^n}\right|\le\frac1{1-\frac{n\,|\delta|}{n-|z+\delta|}}\tag3 $$ Furthermore, $$ \begin{align} \left|\,\arg\left(\frac{\left(1+\frac{z+\delta}n\right)^n}{\left(1+\frac{z}n\right)^n}\right)\,\right| &=n\left|\,\arg\left(\frac{1+\frac{z+\delta}n}{1+\frac{z}n}\right)\,\right|\tag{4a}\\ &=n\left|\,\arg\left(1+\frac{\delta}{n+z}\right)\,\right|\tag{4b}\\[3pt] &\le n\sin^{-1}\left(\frac{|\delta|}{|n+z|}\right)\tag{4c}\\[3pt] &\le\frac\pi2\frac{n\,|\delta|}{n-|z|}\tag{4d} \end{align} $$ Explanation:
$\text{(4a)}$: distribute the exponent
$\phantom{\text{(4a): }}$$\arg\left(z^n\right)=n\arg(z)$
$\text{(4b)}$: simplify the quotient
$\text{(4c)}$: $|\arg(1+z)|\le\sin^{-1}(|z|)$
$\text{(4d)}$: $\sin^{-1}(x)\le\frac\pi2x$ for $0\le x\le1$
$\phantom{\text{(4d):}}$ triangle inequality

For $|\delta|\lt\frac12$ and $n\ge2|z|+1$, $(3)$ gives the thin annulus $$ 1-2|\delta|\le\left|\frac{\left(1+\frac{z+\delta}n\right)^n}{\left(1+\frac{z}n\right)^n}\right|\le\frac1{1-2|\delta|}\tag5 $$ and $(4)$ gives the thin sector $$ \left|\,\arg\left(\frac{\left(1+\frac{z+\delta}n\right)^n}{\left(1+\frac{z}n\right)^n}\right)\,\right|\le\pi|\delta|\tag6 $$ As $\delta\to0$, the intersection of the annulus and the sector tend to $1$:

---

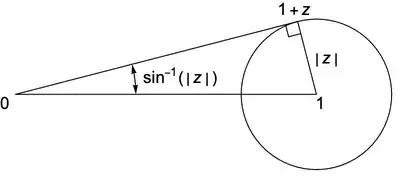
Concerning $\bf{(4c)}$

In the justification of $\text{(4c)}$, it is claimed that $$ |\arg(1+z)|\le\sin^{-1}(|z|)\tag7 $$ As illustrated below, the maximum of $\arg(1+z)$ is attained on the tangent to the circle of radius $|z|$ centered at $1$. In that arrangement, $\arg(1+z)=\sin^{-1}(|z|)$. Symmetry gives $(7)$.

Answer 3

I'm too lazy for inequalities today, so here's an outline. :) If you manipulate the limits, you'll see that you can set $z=0$ without loss of generality. Then it suffices to prove $$n\log\left(1+\frac{z_n}{n}\right)\to0,$$ which follows from $\log(1+x)=x+o(x)$.

Answer 4

A more mundane approach:

Let $f_n(z) = ( 1+{ z \over n})^n$ and note that $f_n(z) \to e^z$ pointwise. We see that $f'_n(z) \to e^z$ and $f''_n(z) = {n-2 \over n} ( 1+{ z \over n})^{n-2}$ and so $|f''_n(z)| \le ( 1+{ |z| \over n})^{n-2} \le e^{|z|}$. In particular, $f''_n(z)$ is bounded on bounded sets (the important part is uniformly in $n$).

Suppose $|w-z| \le 1$ and let $M$ be a bound on $f''_n(w)$, then Taylor's theorem gives us the bound $|f_n(w)-f_n(z)-f'_n(z) (w-z) | \le {1 \over 2} M |w-z|^2$, or $|f_n(w)-f_n(z) | \le {1 \over 2} M |w-z|^2 + |f'_n(z) (w-z)|$. Substituting $w=z_n$ and taking limits we get $f_n(z_n) \to e^z$.