Raising something to an imaginary number is weird, I have a hard time wrapping my head around that.
And $e$ seems even more common and comes up in many situations, such as:
I'd really like to have some light shed on the matter.
How do I begin to form an intuitive grasp of $e^i$ ?
Essentially, the complex exponential characterizes rotations. I will not go into the mathematical "reasons" for why the equations are "true" but rather expand on how to get an intuitive feel for what they mean. This discussion will be quite informal.
The imaginary exponential is characterized by $$e^{iy} = \cos(y) + i\sin(y)$$ where $y\in\mathbb{R}$ and the full exponential can then be defined as $$e^z = e^{x+iy} = e^x\cos(y) + ie^x\sin(y)$$ where I have written $z\in\mathbb{C}$ in terms of its real and imaginary parts $x,\ y\in\mathbb{R}$.
Now complex numbers are really just elements of $\mathbb{R}^2$ imposed with a special structure. So if you regard $e^{iy}$ as a point on the complex plane, you see that the point lies on the unit circle, with coordinates $\left(\cos(y),\ \sin(y)\right)$. More precisely, with our traditional convention of measuring angles counter clock-wise from the positive $x$ (in this case Real) axis, we see that $e^{iy}$ is a point on the unit circle which forms angle $y$ (in Radians) with the positive Real axis.
In this respect, $e^i$ is just a point on the unit circle which is precisely $1$ radian counter clock-wise from the positive real axis. This also helps to explain why $e^{i\pi} = - 1$. A rotation of $\pi$ from the positive real axis is just the opposite side, i.e. the negative real axis.
Now with the full complex exponential, the imaginary part of $z$ signifies the rotational aspect of the number while the real part of the number signifies the magnitude. Each complex number is assigned a magnitude and an angle (called the argument). This is done precisely with the complex exponential.
You may recall that multiplying two complex numbers is equivalent to rotating one number by the angle of the second (and then applying the proper stretches and compressions). But notice that when we rotate something, all we're really doing is adding the appropriate angles together. So complex multiplication is connected to real angle addition. In hindsight, it probably seems natural that the exponential should be somehow related to complex rotations: The map which takes angle to point must satisfy $$f(\theta_1 + \theta_2) = f(\theta_1)f(\theta_2)$$ which is a property which characterizes the exponential function.
The other answers are very nice. I'd just like to add how this works, because it's very nifty and somewhat surprising if you see it the first time. Look at the series definition of $\exp(x)$:
$$ \exp x = \sum_{k=0}^\infty \frac{x^k}{k!} = 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} + \ldots $$
When $x$ is real, this has a fairly simple behavior, it grows monotonously. However, if you allow complex numbers, you can get minus signs in there because of $i^2 = -1$. Let $x = i\alpha$, and then:
$$ \exp i\alpha = \sum_{k=0}^\infty \frac{(i\alpha)^k}{k!} = 1 + i\alpha - \frac{\alpha^2}{2} - i\frac{\alpha^3}{3!} + \frac{\alpha^4}{4!} + i\frac{\alpha^5}{5!} + \ldots $$
Two interesting things happen:
If you collect all the odd terms, which are imaginary, you get:
$$ \mathrm{Im}\,(\exp i\alpha) = \alpha - \frac{\alpha^3}{3!} + \frac{\alpha^5}{5!}- \frac{\alpha^7}{7!}\pm \ldots = \sin \alpha $$ and this happens to be exactly the Taylor expansion of $\sin\alpha$! You start with the value of $\sin(0)=1$ as a first approximation, and keep adding Taylor terms. Since $\sin'0 = \cos 0 = 0 $ there is no $\alpha^1$ term, but $\sin''0 = -1$, so the $\alpha^2$ term is negative, and so on. Every term flips the sign and adds two bends, and you approximate $\sin \alpha$ better and better. A nice picture from the wikipedia article Taylor series:
All the even power terms are real, and they give $\cos \alpha$:
$$ \mathrm{Re}\,(\exp i\alpha) = 1 - \frac{\alpha^2}{2!} + \frac{\alpha^4}{4!} -\frac{\alpha^6}{6!} \pm \ldots = \cos \alpha $$
Which allows you to write the nice formula of Euler:
$$ \exp i\alpha = \cos \alpha + i\sin \alpha $$
As already said in the other answers, you can think of $\alpha$ as the angle from the x-axis (counterclockwise). Since for complex numbers, conventionally $z= x + iy$, it follows that $x = \cos \alpha$ and $y = \sin \alpha$. If I'm doing e.g. some computer graphics calculations, often all I need to remember is "$x = \cos$" and all else falls into place. Another Wikipedia illustration of this:
$e^{i\pi}=-1$ is a special case of
Euler's formula: $e^{i\theta}=\cos{\theta}+i\sin{\theta}$
which you can read about in many, many places. The proof comes from the power series of $e^x$, $\sin{x}$, and $\cos{x}$.
The intuitive way to think about it is the geometric interpretation of the complex numbers as a plane: a real axis and an imaginary axis. (Recall that all complex numbers have the form $a+ib$, for $a,b\in\mathbb{R}$.) Every complex number can also be expressed as $z=|z|e^{i\theta}$ for some $\theta$ (this is essentially polar coordinates).
So, $e^{i\theta}$ represent complex numbers of magnitude $1$, that is, the unit circle on the complex plane.
In this answer, I show that $$ e^{ix}=\lim_{n\to\infty}\left(1+\frac{ix}{n}\right)^n=\cos(x)+i\sin(x) $$ using the geometric properties of complex multiplication. It is argued there that, as shown in this answer, since $$ \lim_{x\to0}\frac{\tan(x)}{x}=1 $$ and $$ \lim_{n\to\infty}\left(1+\frac{x^2}{n^2}\right)^{n/2}=1 $$ that the product of $n$ copies of $1+ix/n$
$\hspace{5cm}$
that is, $$ \lim_{n\to\infty}\left(1+\frac{ix}{n}\right)^n $$ has length $1$ and argument $x$, which means that it equals $$ \cos(x)+i\sin(x) $$
Well do you know the power series of the exponential function? $$\exp(x)=\sum_{k=0}^\infty \frac{x^k}{k!}=1+x+\frac{x^2}{2}+\frac{x^3}{3\cdot 2}+\dots$$ And in Special $$\exp(ix)=\cos(x) + i \sin(x)$$ The $e$ function is so common because it is the only function which holds $$f'(x)=f(x) \quad f(0)=1$$ for all $x$
From @in_wolfram_we_trust's comment with link to a good explanation the key point for me was:
imaginary exponential growth continuously rotates a number
(This made the whole thing click for me, and none of the three answers so far have expressed it in such direct terms.)
Personally, my intuition for the complex exponential $x\mapsto e^{ix}$ is Lie-theoretic.
A smooth manifold is a topological space which is locally diffeomorphic to Euclidean space; a group is a set with an associative binary operation, inverses and an identity (often we speak of it encoding some form of symmetry; the collection of transformations which preserve a set of properties of a given object, if closed under multiplication and inverses, is a group); a space that is both a smooth manifold and a group in which multiplication and taking inverses are smooth maps is called a Lie group; the tangent space of the identity element (which will become equipped with a 'bracket' operation, but this operation is trivial if our group is abelian) is called a Lie algebra.
The circle group, as a subspace of the complex plane, is clearly a one-dimensional Lie group, and its Lie algebra is therefore a line, so in particular $\cong\bf R$. The preceding paragraph invokes a lot of heavy language to deal with what is essentially a very simple object; placing this example in perspective is something I find helpful though. For any tangent vector $X$ in the Lie algebra / tangent space, there is a unique one-parameter subgroup in the Lie group which, as a curve, has the given tangent vector at the identity. The exponential $\exp(tX)$ is defined to parametrize this curve.
Suppose our Lie group is realized concretely as a matrix group (see e.g. Ado's theorem). Then the tangent space is also a subspace of matrices, and the exponential map satisfies $\Phi'(t)=X\Phi(t)$, where $\Phi(t)=\exp(tX)$, which can be deduced using $\Phi(t+h)=\Phi(t)\Phi(h)$ and $\Phi'(0)=X$. Some calculus tells us we have $\exp(tX)=\sum_{n\ge0}(tX)^n/n!$. Then, using complex numbers and their multiplication as an acceptable substitute for our $2\times2$ matrices, the tangent space of $1$ on the unit circle is identified with the imaginary axis $i\bf R$, and our exponential is in fact $\exp:x\mapsto e^{ix}$.
The mystery, then, lies in how a geometrically-inspired "exponential map" manifests as a number being raised to powers (i.e. a bona fide exponential); this is not so mysterious, though, when we consider the fact that our $\exp$ (when restricted to linear subspaces of the Lie algebra; we actually don't have $\exp(AB)=\exp(A)\exp(B)$ in general - see the BCH formula) is an additive group homomorphism, exactly as a bona fide exponential.
Geometrically, $ze^{i \phi}$ rotates the complex number $z$ by $\phi$ radians. In terms of rotation, $e$ makes it so that if $\phi = 2 \pi$ (a full rotation), then $z e^{i \phi}$ rotates $z$ right back to where it started. In other words, $e^{i 2 \pi}=1$. Otherwise you can use any base you want. I am not sure, but complex exponentiation may have been defined this way so that the ideal properties of having $e$ as a base could be taken advantage of for calculus (such as, obviously, $\int e^x dx= e^x$).
$i$ itself can be considered a "rotating abstract plane with rotating force $\frac 1 2 \pi$". When you either multiply an object by $i$ or take it to the power of $i$, you are rotating that object. So when you take a number such as 5 and you multiply it by $i$, you have in essence rotated it by $\frac 1 2 \pi$ (which is 90 degrees). That's why, geometrically, you start with 5 on the $x$ axis at the point (5,0) but $5i$ is on the $y$ axis at the point (0,5), having been rotated $\frac 1 2 \pi$ radians.
Let's say you start with 1, and rotate it by $\frac 1 2 \pi$ radians. This would be written $1 i=i$, or $1e^{i \frac 1 2 \pi}=e^{i \frac 1 2 \pi}$. Then we want to rotate it by another $\frac 1 2 \pi$ radians. This would be written $i i=i^2$, or $e^{i \frac 1 2 \pi}e^{i \frac 1 2 \pi}=e^{i 2\frac 1 2 \pi}=e^{i \pi}$ (That is, $i^2=e^{i\pi}$. They both represent the same rotation).
And so what we've done, after starting with the complex number 1, is rotate by a full $\pi$ radians (which is 180 degrees). If we rotate the point (1, 0) by 180 degrees about the origin, we get to the point (-1, 0). This is why, geometrically, $ii=i^2=-1$; as well as why $e^{i \pi}=-1$. Both of these represent a rotation by 180 degrees, which, if it helps, you can think of as the same thing as multiplying the real and imaginary components of the complex number by -1.
You can think of any complex number $a + bi$ as a real matrix $\begin{pmatrix}a & b \\ -b & a \end{pmatrix}$. (You have to replace exponential function by matrix exponential, but in terms of the series expansion that's the same).
It's clear that $i$ is a $\pi/2$ rotation (-matrix), according to the comment's above. It's further clear that $i^2$ is $-1$, and so on. For me, this helped me understanding that imaginary numbers are an extension of the real numbers.
Note: not every matrix is allowed! Only matrices of the given specific form are allowed - but all operations you want to make (exponential, inverse, multiply by scalar, add, ...) will yield matrices of that form.
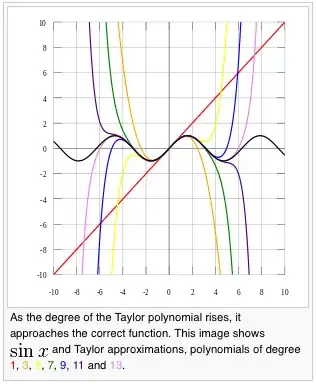
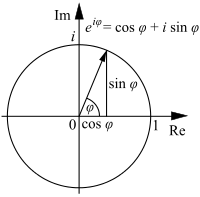
I'm with you on the infinite series thing. I find it perfectly rigorous, but unimpressive from an intuitive point of view.
Here's yet another way to think about $e^z$, which may or may not help you.
We can think of the exponential function $\exp : R \rightarrow R$ as the unique analytic function with the following properties:
$$\exp(0) = 1$$ $$\frac{d}{dx}\exp(x) = \exp(x)$$
You do need a bit of calculus to show that the function exists and is unique. You can prove this if you wish, or we can just take it as read.
Is there an obvious way to extend this function to the complex plane?
We will assume that $\exp(ix)$ is a complex-valued function. We will introduce two real-valued functions to represent the real and imaginary parts:
$$c : R \rightarrow R$$ $$s : R \rightarrow R$$ $$\exp(ix) = c(x) + i s(x)$$
Of course we know the reason for calling them $c$ and $s$, but let's pretend we don't, and just assume they're analytic functions, and see what we can find out about them.
Setting $x=0$ gives:
$$c(0) = 1$$ $$s(0) = 0$$
So far, so good. We would also like to preserve the property:
$$\frac{d}{dx}\exp(x) = \exp(x)$$
That is:
$$c(x) + i s(x) = \exp(ix) = i \exp'(ix) = i c'(x) + i^2 s'(x) = - s'(x) + i c'(x)$$
Note that again, no additional properties of $\exp$ are assumed beyond those we already gave. The second step uses the chain rule, but this is okay because we assumed $\exp$ was analytic.
Matching up real and imaginary components gives:
$$c(x) = - s'(x)$$ $$s(x) = c'(x)$$
So we have a coupled system of differential equations, and we also have initial conditions at $x=0$. Again, you need some calculus to show that $c$ and $s$ exist and are unique. The solution, of course, turns out to be $c(x) = \cos x$ and $s(x) = \sin x$.
One last thing you should know.
The exponential identity is useful for deriving almost every trigonometric identity that you will ever need. That, and Pythagoras' theorem ($\cos^2 \theta + \sin^2 \theta = 1$).
Suppose, for example, you need a formula for $\sin (a+b)$. Then:
$$\cos (a+b) + i \sin(a+b) = e^{i(a+b)} = e^{ia} e^{ib}$$ $$= ( \cos a + i \sin a ) (\cos b + i \sin b )$$ $$= \cos a \cos b + i \cos a \sin b + i \sin a \cos b - \sin a \sin b$$ $$= (\cos a \cos b - \sin a \sin b) + i (\cos a \sin b + \sin a \cos b)$$
Matching up real and imaginary parts gives:
$$\cos (a+b) = \cos a \cos b - \sin a \sin b$$ $$\sin (a+b) = \cos a \sin b + \sin a \cos b$$
$e^i$ is a unit vector whose angle with the real axis in the complex plane is $1$ radian.
See the Math Java Applet in http://basic-electronics.com/euler/ for a alternative and intuitive idea of $e^{i\pi}+1=0$. And here for a Visual Derivation of Euler's Formula.
Recall that $e^x$ can be defined as the limit as $\epsilon$ approaches 0 of $(1 + \epsilon \cdot x)^{1/\epsilon}$. If $x$ is a real number, like $1$, then we can think of this intuitively as the product of infinitely many values that are infinitesimally larger than $1$. Multiplying by a value that's larger than $1$ moves you away from the origin, so naturally, the end result, $e^1$, is a real number significantly greater than $1$.
But what if $x$ is an imaginary number, like $i$? We can think of $e^i$ as the product of infinitely many values of the form $(1 + \epsilon \cdot i)$, where $\epsilon$ is infinitesimal. Multiplying by such a value moves you counterclockwise around the origin, and so the end result, $e^i$, is still at a distance of $1$ away from the origin, but now it's counterclockwise of where you started.
An an approximation, try evaluating $(1 + 0.001 i)^{1000}$. Each factor of $(1 + 0.001 i)$ moves you an insignificant distance farther from the origin, but it also moves you a significant distance around the origin. So you end up with $r$ very close to $1$, and with $\theta$ very close to $1$ as well. If you look at $e^i$, then $r$ and $\theta$ are both exactly equal to $1$.
I think you have problem with understanding what exactly is meant by $e^{i}$ rather than formulas to compute.
In that case we have problems to intuitively understand what exactly is $a^x$ when the domain is $\mathbb{R}$ .This can be easily understood when the domain is integers. For eg: $a^2=a*a$ multiplying by $n$ times the number $a$ which is called as the base. We can also define the same thing similarly when $n$ is a rational number. But how can we define what exactly is $a^{\sqrt{2}}$ or $a^{\sqrt{\sqrt[3]{3}+\sqrt[5]{5}}}$ The same problem like raising to an imaginary number occurs.
But we can simply avoid such problems by defining logarithm and then using that to define what is $a^x$. Once you get the definition of $a^x$ with domain real numbers . The extension to imaginary numbers is easy .
