Finding out the argument a complex number

Question

So this is something I'm still having issues with. Lets say I have the following: $$z^6 = -8$$ Now if I take $\frac{1}{6}$ power on both sides, I get $z = \sqrt{2}i$. Now, if I look at the point that this is in, I mean the value for the real number is $0$ so it must be at angle $\frac{\pi}{2}$ right? For some reason though, it should be the $arg(z) = \frac{\pi}{6} + \frac{\pi}{3}k$ which I don't quite understand. Would appreciate some help, thanks in advance!

Answer 1

$$z^6=-8=2^3e^{i\pi}=2^3e^{(2n+1)\pi i}$$ where $n$ is any integer

$$\implies z=2^{3/6}e^{(2n+1)\pi i/6}$$ where $n=0,1,2,3,4,5$

Answer 2

Yes, your calculation is correct, as we can see by calculating: $(\sqrt(2) i)^6 = (-2)^3 = -8$

However, when we calculate roots of complex numbers the number of roots, there are always $n$ $n$th roots (This result is related to the Fundamental Theorem of Algebra). That is there are $2$ square roots, $3$ cube roots and so on.

In thus case, there are 6 roots and you haver successfully calculated one of them. In particluar, $\sqrt{2} i $ is a root lying on the X-axis with argyment $\pi /2 $.

The other roots all lie at intervals of $\pi /3$ or $60$ degrees from this root.

To calculate them all, note thta we are trying to solve

$z^6 = -8$

Now, $ z = (-8)^{\frac{1}{6}} = (-1)^{1/6} 8^{1/6} = \sqrt{2} \cdot (e^{(2n+1)\pi i})^{1/6} = \sqrt{2} \cdot e^{i \frac{(2n+1) \pi}{6}} $

Thus, $\arg (z) = {(2n + 1) \pi}{6} = \frac{\pi}{6} + n \cdot \frac{\pi}{3}$ as required.

Note that, we can set $n = 0,1, \dots , 5$ and get the required solutions:

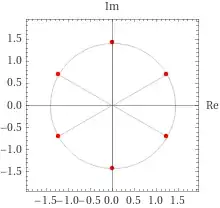
$z = \sqrt{2} e^{i \frac{\pi}{6}}, \sqrt{2} e^{ i \frac{ 3\pi }{6} }, \sqrt{2} e^{i \frac{5\pi}{6}}, \sqrt{2} e^{i \frac{9\pi}{6}}, - \sqrt{2} i, \sqrt{2} e^{i \frac{11\pi}{6}}$

You can see the $6$ sextic roots of $(-1)$ graphically using the complex plane: