I need to find an expression for $n$th derivative of $f(x) = e^{x^2}$. Really need help.
Asked
Active
Viewed 1.0k times
29
-
7Can you find the first few derivatives yourself? – Ben Millwood Sep 10 '12 at 17:43
-
I already did, but I can't see the patern – Mykolas Sep 10 '12 at 17:46
-
7Nevertheless, you'll find people much more willing to help you if you show that you've done some work yourself - besides, someone else might be able to see the pattern. – Ben Millwood Sep 10 '12 at 17:57
-
8http://en.wikipedia.org/wiki/Hermite_polynomials – Hans Lundmark Sep 10 '12 at 18:03
-
3try taking derivative of taylor expansion of $e^{x^2}$ – S L Sep 10 '12 at 18:05
-
also if you feel bored you can plugin for those stuff into WA .... I was kinda looking myself. – S L Sep 10 '12 at 18:06
-
For this kind f question it often help to use logarithmic differentiation: – kjetil b halvorsen Sep 10 '12 at 19:05
-
4More generally, $$ \frac{d^n}{dx^n}e^{x^p} = \left(\sum_{k \in \mathbb{Z}}a_{n,k;p}x^{kp-n} \right) e^{x^p} $$ where the coefficients $a_{n,k;p}$ form the exponential Riordan array $A_p = [1, (1+x)^p - 1]$. This can be proved using some of the techniques from http://math.stackexchange.com/questions/18284 and is given as an exercise (although not in those terms) in Comtet's Advanced Combinatorics. – Peter Taylor Sep 10 '12 at 19:52
9 Answers
34
Here is a less elementary solution.
We consider the exponential generating function
$$G(t,x) = \sum_{n=0}^{\infty} \frac{t^n}{n!} \frac{d^n}{dx^n}e^{x^2}.$$
Then we can identify this series as the McLaurin series of $e^{(x+t)^2}$ near $t = 0$. Thus we must have
$$G(t,x) = e^{(x+t)^2} = e^{x^2} e^{2xt} e^{t^2} = e^{x^2}\left( \sum_{k=0}^{\infty} \frac{(2x)^k}{k!} t^k \right)\left( \sum_{l=0}^{\infty} \frac{1}{l!} t^{2l} \right). $$
Expanding this series and comparing, we have
$$ \frac{d^n}{dx^n} e^{x^2} = \left( \sum_{j=0}^{\lfloor n/2 \rfloor} \frac{n!}{j!(n-2j)!}(2x)^{n-2j} \right) e^{x^2}. $$
Here is an example:
Sangchul Lee
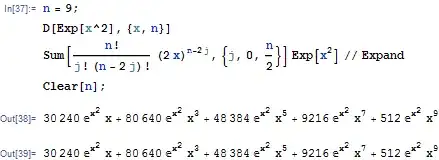
- 167,468
-
1I love this, particularly because my intuition was that a closed form expression using only simple operations like factorial would not be possible. – 2'5 9'2 Sep 10 '12 at 18:46
-
It would be even simpler to use the Hermite polynomials for this, no? – J. M. ain't a mathematician Sep 12 '12 at 02:22
-
@J.M., Unfortunately I know not much about the Hermite polynomials. I have heard of these polynomials, and also know that they are closely related to the Gaussian-weighted $L^2$ space, but the important thing is that I even do not know the exact definition or a representation formula for this nice family. That's why I just made a rather elementary approach. – Sangchul Lee Sep 12 '12 at 02:37
-
2In that case, you'll want to see the Rodrigues formula for the Hermite polynomials. Notice anything? ;) – J. M. ain't a mathematician Sep 12 '12 at 02:42
-
2@J.M., Now it's also clear to me! We may write $$\frac{d^n}{dx^n}e^{x^2} = i^{-n}H_n(ix)e^{x^2}.$$ – Sangchul Lee Sep 12 '12 at 02:46
-
-
I expanded the series but faild with comparing , how you get the result of comparing , can you help ? – Sep 12 '14 at 01:07
-
This same approach could be used in the $e^{-x^2}$ case to derive the explicit expression for the Hermite polynomials. +1 – WillG Aug 19 '21 at 15:55
13
I'm not sure if this is what you are after, but there is a recursion that you can establish. Each derivative will be the product of a polynomial in $x$ with $e^{x^2}$. If $f^{(n)}(x)=p_n(x)e^{x^2}$, then we have $$p_0(x)=1$$ and $$p_n(x)=2x\,p_{n-1}(x)+p^\prime_{n-1}(x)$$
This recursion has the following associated infinite matrix:
$$M=\begin{bmatrix} 0 & 1 & 0 & 0 & \cdots\\ 2 & 0 & 2 & 0 & \cdots\\ 0 & 2 & 0 & 3 & \cdots\\ 0 & 0 & 2 & 0 & \cdots\\ \vdots & \vdots & \vdots & \vdots & \ddots\\ \end{bmatrix}$$
viewed as a transformation on the vector space of polynomials in $x$ with basis $\left\{1,x,x^2,x^3,\ldots\right\}$. The first column of $M^n$ gives you the $n$th derivative of $f$. If there is any hope to solve the recursion explicitly (which I'm not optimisitic for) then I'd recommend further study of this matrix. Maybe it can be diagonalized, and that would give way to a formula for $f^{(n)}$.
-
-
Moreove, $p_n(x) = x g_n(x^2)$ for $n$ odd and $p_n(x)=h_n(x^2)$ for $n$ even. – lhf Sep 10 '12 at 18:08
-
-
1
8
Let $y=e^{x^2}$. We want to find $\frac{d^n y}{dx^n}$.
Note that $\ln y = x^2$ and so $\frac{1}{y} \frac{dy}{dx} = 2x\iff \frac{dy}{dx}=2xy$.
Differentiating again yields:
$\frac{d^2y}{dx^2}=2x\frac{dy}{dx}+2y$,
$\frac{d^3 y}{dx^3} = 2x \frac{d^2 y}{dx^2} + 4\frac{dy}{dx}$,
$\frac{d^4 y}{dx^4} = 2x \frac{d^3 y}{dx^3} + 6\frac{d^2 y}{dx^2}$.
We might guess that $\frac{d^n y}{dx^n} = 2x \frac{d^{n-1} y}{dx^{n-1}}+2(n-1) \frac{d^{n-2} y}{dx^{n-2}}$, which is easily proved by straightforward induction (we leave this as an exercise to the reader. ;) )
Let $u_k=\frac{d^k y}{dx^k}$ for easier notation. We thus have established
$u_n = 2x u_{n-1}+2(n-1)u_{n-2}$.
It is easy to find that the coefficient of $x^n y$ in $u_n$ is $2^n$, but I'm not seeing any nice way of solving the recursion at the moment.
Daniel Fischer
- 206,697
Is Ne
- 2,668
5
Another approach is to write:$$f(x+y)=\sum_{n=0}^\infty \frac{f^{(n)}(x)}{n!} y^n$$
Now $f(x+y)=f(x)f(y)e^{2xy}$. So if we let $g_n(x)=f^{(n)}(x)/f(x)$ then we see that:
$$f(y)e^{2xy} = \sum_{n=0}^\infty \frac{g_n(x)}{n!}y^n$$
But $$f(y)=\sum_{k=0}^\infty \frac{1}{k!} y^{2k}$$ and $$e^{2xy} = \sum_{m=0}^\infty \frac{(2x)^m}{m!}y^m$$
So:
$$f(y)e^{2xy} = \sum_{n=0}^\infty \frac{y^n}{n!} \sum_{m+2k=n} \frac{(2x)^m n!}{m!k!}$$
which gives us $$g_n(x)=\sum_{m+2k=n} \frac{(2x)^m n!}{m!k!}=\sum_{k=0}^{\lfloor n/2\rfloor}\frac{2^{n-2k}n!}{(n-2k)!k!}x^{n-2k}$$
And $f^{(n)}(x)=f(x)g_n(x)$.
Thomas Andrews
- 177,126
-
Well, I see @sos440 beat me to this answer, but since my answer is slightly organized differently, I'll leave it as is. – Thomas Andrews Sep 10 '12 at 19:27
1
The derivatives at $0$ may be found simply using the Taylor expansion: $$e^x = \sum_{k=0}^\infty {\frac{x^k}{k!}}$$ So that: $$e^{x^2} = \sum_{k=0}^\infty {\frac{x^{2k}}{k!}} = \sum_{k=0}^\infty {\frac{x^{k}}{k!}f^{(k)}(0)}$$ Leading to: $$f^{(2n)}(0) = {(2n)! \over n!} , \ f^{(2n+1)}(0) = 0$$ This means that for $f^{(n)}(x) = p_n(x) e^{x^2} = (\sum a^{(n)}_k x^k) e^{x^2}$:
$$a^{(2n)}_0 = {(2n)! \over n!}, \ \ a^{(2n + 1)}_0 = 0$$ And using alex's recursion: $$a^{(2n - 1)}_1 = {(2n)! \over n!}$$
Nathaniel Bubis
- 33,018
-
-
$$e^{x^2} = \sum_{k=0}^\infty {\frac{x^{2k}}{k!}} = \sum_{k=0}^\infty {\frac{x^{k}}{k!}f^{(k)}(0)}$$ – Mykolas Sep 10 '12 at 19:21
-
-
-
But this will only give an good approximation when x is close to zero, isn't it? – skan Apr 25 '20 at 15:17
1
Related problems (I), (II), (III), (IV), (V), (6), (7). I already posted a solution on this website related to this one.
Here is the first formula, which gives only the $n$th derivative of integer order of ${\rm e}^{x^2}$
$$ {{\rm e}^{{x}^{2}}}\sum _{s=0}^{n} \left( {x}^{2\,s-n}\sum _{k=0 }^{n}{2}^{k+s} \left[\matrix{n\\k+s}\right] \left\{\matrix{k+s\\s}\right\} \right)\,, $$
where $\left[\matrix{n\\k+s}\right]$ and $\left\{\matrix{k+s\\s}\right\}$ are the Stirling numbers of the first kind and the second kind respectively.
The second formula is more general. It is a unified formula for the $n$th derivative and the $n$th anti derivative of real orders (including integer orders) of ${\rm e}^{x^2}$ in terms of the Meijer $G$-function,
$$ \left( -1 \right)^{\frac{n}{2}}{2}^{n} G^{1, 2}_{2, 3}\left(-{x}^{2}\, \Big\vert\,^{-\frac{n}{2}, -\frac{n}{2}+\frac{1}{2}}_{-\frac{n}{2}, \frac{1}{2}, 0}\right)\,.$$
Note that,
(i) if $n > 0$, then the formula gives derivatives of order $n$ ($n$ can be integer or real ).
(ii) if $ n<0 $, then the formula gives anti-derivatives of order $n$ ($n$ can be integer or real).
(iii) if $n=0$, then it gives the original function.
Mhenni Benghorbal
- 47,431
1
I love to see questions like this in patterns/scheme. After the already given complete answers (especially the comment of Peter Taylor contains a very nice formal statement) here one more version, but which focuses on the visibility of the pattern in the coefficients. In Pari/GP I simply called
(exp(x^2) ) / exp(x^2)
(exp(x^2) ') / exp(x^2)
(exp(x^2) '' ) / exp(x^2)
(exp(x^2) ''' ) / exp(x^2)
with so many apostrophes as needed for the n'th derivative. In the result
1 + O(x^34)
2*x + O(x^33)
2 + 4*x^2 + O(x^32)
12*x + 8*x^3 + O(x^31)
12 + 48*x^2 + 16*x^4 + O(x^30)
120*x + 160*x^3 + 32*x^5 + O(x^29)
120 + 720*x^2 + 480*x^4 + 64*x^6 + O(x^28)
1680*x + 3360*x^3 + 1344*x^5 + 128*x^7 + O(x^27)
1680 + 13440*x^2 + 13440*x^4 + 3584*x^6 + 256*x^8 + O(x^26)
I find the pattern:
1 = exp(x^2)/exp(x^2)
2*x = exp(x^2)'/exp(x^2)
2* 1* 1 + 4*x^2 = exp(x^2)''/exp(x^2)
2* 2* 3*x + 8*x^3 = ...
3*4* 1* 1 +2* 4* 6*x^2 + 16*x^4 = ...
3*4* 2* 5*x +2* 8*10*x^3 + 32*x^5 = ...
4*5*6* 1* 1 + 3*4* 4*15*x^2 +2*16*15*x^4 + 64*x^6 = ...
4*5*6* 2* 7*x + 3*4* 8*35*x^3 +2*32*21*x^5 +128*x^7 = ...
After that I find it obvious how this continues (formal description&proof are in the other answers above) and leave that schematic description just for the accidental later reader here.
Gottfried Helms
- 34,920
1
The values of the derivatives all multiplied by a factor of $e^{x^2}$ are
$2x$
$2 + 4x^2$
$8x + 4x + 8x^2 = 12x + 8x^2$
$12 + 16x + 24x^2 + 16x^3 $
The if this polynomial progression is called $Q(n)$ the general pattern is:
$Q(n+1) = Q'(n) + 2xQ(n)$ where $Q(0) = 1$
Sidharth Ghoshal
- 16,771
0
A general formula \begin{equation*} \bigl(e^{x^\alpha}\bigr)^{(n)} =e^{x^\alpha}\sum_{k=0}^n x^{k\alpha-n} \sum _{j=k}^n s(n,j)\alpha^jS(j,k), \quad n\ge0 \end{equation*} was established at the site https://math.stackexchange.com/a/4262657/945479. See also https://math.stackexchange.com/a/4261764/945479, https://math.stackexchange.com/a/4263059/945479, and https://math.stackexchange.com/a/4263062/945479.
In particular, we obtain \begin{equation*} \bigl(e^{x^2}\bigr)^{(n)} =e^{x^2}\frac{n!}{(2x)^n} \sum_{k=0}^{n}\binom{k}{n-k}\frac{(2x)^{2k}}{k!}. \end{equation*}
References
- F. Qi and B.-N. Guo, Explicit formulas for special values of the Bell polynomials of the second kind and for the Euler numbers and polynomials, Mediterr. J. Math. 14 (2017), no. 3, Art. 140, 14 pages; available online at https://doi.org/10.1007/s00009-017-0939-1.
- F. Qi and M.-M. Zheng, Explicit expressions for a family of the Bell polynomials and applications, Appl. Math. Comput. 258 (2015), 597--607; available online at https://doi.org/10.1016/j.amc.2015.02.027.
- Feng Qi, Da-Wei Niu, Dongkyu Lim, and Yong-Hong Yao, Special values of the Bell polynomials of the second kind for some sequences and functions, Journal of Mathematical Analysis and Applications 491 (2020), no. 2, Paper No. 124382, 31 pages; available online at https://doi.org/10.1016/j.jmaa.2020.124382.
- Siqintuya Jin, Bai-Ni Guo, and Feng Qi, Partial Bell polynomials, falling and rising factorials, Stirling numbers, and combinatorial identities, Computer Modeling in Engineering & Sciences 132 (2022), no. 3, 781--799; available online at https://doi.org/10.32604/cmes.2022.019941.
qifeng618
- 1,691