96

The Pythagorean Theorem is one of the most popular to prove by mathematicians, and there are many proofs available (including one from James Garfield).

What's the most elegant proof?

My favorite is this graphical one:

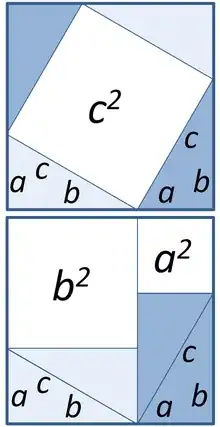
alt text

According to cut-the-knot:

Loomis (pp. 49-50) mentions that the proof "was devised by Maurice Laisnez, a high school boy, in the Junior-Senior High School of South Bend, Ind., and sent to me, May 16, 1939, by his class teacher, Wilson Thornton."

The proof has been published by Rufus Isaac in Mathematics Magazine, Vol. 48 (1975), p. 198.

Martin Sleziak
  • 53,687
Shane
  • 111

17 Answers17

75

I really like this one (image taken from cut-the-knot #4)

alt text

along with

$$(a+b)^2 = 4\cdot\frac{1}{2}a b + c^2$$ $$\Leftrightarrow c^2 = a^2 + b^2$$

It's so clear and easy ...

Note: Just to make it clear, the side of the square is a+b

NoChance
  • 6,427
Dario
  • 2,614
  • 8
    I would like to point out that the fact that the area of a rectangle is the product of the lengths of its sides is not trivial. Indeed, it's not even meaningful until you make sense of the notion of multiplying irrational numbers and justify that the usual algebraic rules apply to them. The elegance of this proof could be seen as an example of the power of the real number system. – Jack M Jun 16 '13 at 02:50
  • 3
    @JackM Here is a proof by Euclid that the area of a rectangle is length times width: aleph0.clarku.edu/~djoyce/java/elements/bookVI/propVI14.html It's phrased in really archaic language, but it basically says this: two equiangular parallelograms (I.e. rectangles) with dimensions $l_1$ and $w_1$ and $l_2$ and $w_2$ respectively have equal area if and only if the ratio of $l_1$ to $w_2$ is equal to the ratio of $l_2$ to $w_1$ (which we would write as $l_1w_1 = l_2w_2$). It relies on Eudoxus' theory of proportions, which was Dedekind's inspiration for his Dedekind cut construction. – Keshav Srinivasan Oct 27 '13 at 01:18
  • @JackM I found a proposition of Euclid that seems to demonstrate even more directly that area = length times width: aleph0.clarku.edu/~djoyce/java/elements/bookVI/propVI1.html – Keshav Srinivasan Nov 16 '13 at 17:03
50

The proof that uses the fact that shearing a parallelogram parallel to one of its sides preserves area is my favorite. Here's an animation from this site:

animated proof

Asaf Karagila
  • 393,674
Isaac
  • 36,557
40

More than dissection proofs, I find the proof using similarity most enlightening and intuitive. See post by Terence Tao: drop a perpendicular from C to the hypotenuse AB.

Image from Tao

In the figure, the triangles whose are areas are marked x and y are similar to the original triangle (which has area x+y). So accepting that areas of similar right-angled triangles are proportional to the squares of the hypotenuse, x:y:x+y are in ratio a2:b2:c2, which is Pythagoras's theorem.

See also the linked discussion by Alexander Giventhal where he remarks that this proof is more general than tiling or dissection proofs, and is even proved by Euclid. If you think of a2+b2=c2 as the geometrical result that the sum of areas of squares constructed with sides a and b is the area of a square placed on c, then the Pythagorean theorem is true not just for constructing squares on the sides, but any similar figures. For instance, as Euclid himself proves, something like the following is true (though it's still just saying a2+b2=c2):

From Giventhal

Community
  • 1
ShreevatsaR
  • 41,374
39

I think this proof is pretty water tight!

Proof of Pythagorean theorem

James Fennell
  • 807
  • 35
    How do we know that the tanks all have equal depth?! Trickery, I tells you! Trickery! – user642796 Dec 16 '12 at 13:17
  • 14
    This works for triangles of only one shape. – Michael Hardy Jan 22 '13 at 18:11
  • 9
    To make sure this is a general proof (and not a proof for one specific case) you'd need infinite ammounts of these contraptions, one for each possible triangle. – Dakkaron Feb 17 '14 at 08:42
  • What is the name of the blue liquid used here? – HeWhoMustBeNamed Oct 15 '17 at 10:31
  • 2
    Not really a mathematical proof, but +1 anyway because it's cool to watch. – Oscar Lanzi May 12 '18 at 16:02
  • I don't think of this as I know the Pythagoren theorem is true because I watched this demonstration. I think of this as I already figured out a proof that the answer to both of my questions at https://math.stackexchange.com/questions/3102944/existence-and-uniqueness-of-function-satisfying-intuitive-properties-of-distance are yes and I see that this demonstration matches the prediction. I love being smart enough to think of it that way and to check by other methods that the theory indeed does predict this observation. – Timothy Aug 18 '19 at 02:35
  • There is nothing wrong with this demonstration: the liquid flows through the holes at hypotenuse's corners. Gravity settles the scores. – Hulkster Mar 27 '23 at 13:25
22

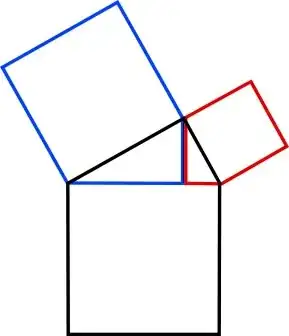
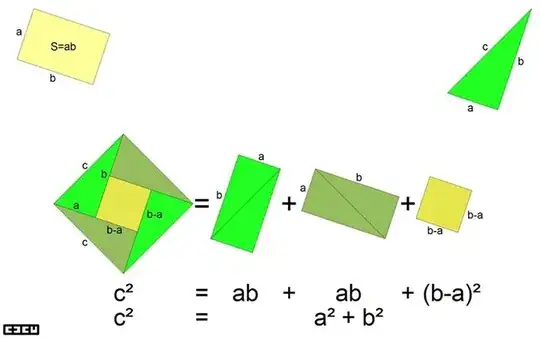
My favorite proof of the Pythagorean Theorem is a special case of this picture-proof of the Law of Cosines:

Proof Without Words: The Law of Cosines

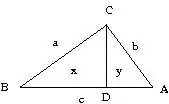
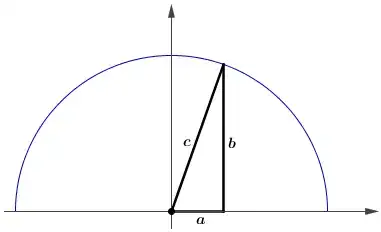
Drop three perpendiculars and let the definition of cosine give the lengths of the sub-divided segments. Then, observe that like-colored rectangles have the same area (computed in slightly different ways) and the result follows immediately.

When C is a right angle, the blue rectangles vanish and we have the Pythagorean Theorem via what amounts to Proof #5 on Cut-the-Knot's Pythagorean Theorem page. (Note that, as mentioned on CtK, the use of cosine here doesn't amount to an invalid "trigonometric proof".)

The picture works for obtuse C as well. (Proof left as an exercise for the reader.)

A final note ... Because the same-colored rectangles have the same area, they're "equidecomposable" (aka "scissors congruent"): it's possible to cut one into a finite number of polygonal pieces that reassemble to make the other. While there's at least one standard procedure for determining how to make the cuts, the resulting pieces aren't necessarily pretty. Some popular dissection proofs of the Pythagorean Theorem --such as Proof #36 on Cut-the-Knot-- demonstrate a specific, clear pattern for cutting up the figure's three squares, a pattern that applies to all right triangles. I have yet to find a similarly straightforward cutting pattern that would apply to all triangles and show that my same-colored rectangles "obviously" have the same area.

(Another exercise for the reader, perhaps? :)

Blue
  • 75,673
  • Yes, of course. Here's a picture for you in return. – t.b. Jul 31 '11 at 23:51
  • 1
    Are you saying it is your favorite proof because it kills two birds with one stone? – StudentofEuler2718 Aug 04 '13 at 17:30
  • 1
    Cay you define those trigonometric functions and prove their properties, without use of the Pythagorean theorem? – Hulkster Apr 01 '23 at 21:20
  • @Hulkster: I'm simply invoking cosine as a convenient shorthand for the standard "adjacent over hypotenuse" ratio in a right triangle, and leveraging the proportionality of lengths in similar (right) triangles. There is no appeal (explicit or implicit) to the Pythagorean theorem (or its trig-identity form, $\sin^2\theta+\cos^2\theta=1$), so there's no circular reasoning here. – Blue Apr 01 '23 at 21:39
20

Every time you walk on a floor that is tiled like this, you are walking on a proof of the Pythagorean theorem. Floor tiled with two sizes of square tiles

If you consider say the upper left corner of every small tile, you can see that these points lie on a periodic grid (shown in red). Each square in this grid is $c \times c$. Then you can choose either of two easy proofs:

(1) The $c \times c$ square is clearly a rearrangement of one $b \times b$ square and one $a \times a$ square.
- or -
(2) Each period of the periodic pattern covers what area of floor? On the one hand there is one $a \times a$ square and one $b \times b$ square per period, while on the other hand there is one $c \times c$ square per period.

(The second one is my favorite, since unlike most proofs it requires neither dissection nor algebra. You don't even need the red or blue lines: Once you see the tiling's periodicity, just note that it is $c \times c$ and you are done!)

Matt
  • 9,223
  • I thought Dario's was unbeatable for its simplicity but this one is even more elegant, especially option (2)! Thank you. – ProfDFrancis Feb 27 '20 at 00:39
17

Three similar houses. The red and the blue gables together make up the black one; therefore the same is true for the square side walls.

enter image description here

Christian Blatter
  • 226,825
13

This is not really a proof, in the sense that it depends on certain physical assumptions, but it forces you to think very hard about what those physical assumptions are. I learned it from Mark Levi's The Mathematical Mechanic, although unfortunately I don't have a diagram.

Consider a fish tank in the shape of a triangular prism, where the triangle on top has vertices $A, B, C$ ($C$ is the right angle) and the triangle on the bottom has opposite vertices $A', B', C'$. Let $a, b, c$ denote the lengths of the opposite sides. Run a rod through the edge $A A'$ on which the fish tank is allowed to pivot, and fill it with water. By conservation of energy, this system is in mechanical equilibrium.

On the other hand, I claim (and it is not hard to see) that the total torque about the rod is proportional to $c^2 - b^2 - a^2$, each contribution coming from the pressure of the water in the tank against the corresponding side.

Qiaochu Yuan
  • 419,620
10

From the first six books of the elements of Euclid by Oliver Byrne:

Pages 48 and 49 of the book

MvG
  • 42,596
10

This animated gif demonstrates the proof eloquently.

enter image description here

Robert Harvey
  • 170
7

In my opinion, one of the most elegant is the "calculus proof" by John Molokach:

Given a right triangle with legs $a$ and $b$ and hypotenuse $c$, construct a semicircle in a rectangular coordinate system like the picture below.

calculus proof Pythagorean theorem

The function $y$, whose graph is the semicircle, satisfies the IVP $$\left\{\begin{align} &y'=-x/y\\ &y(0)=c \end{align}\right.$$ The solution of this IVP is $y(x)^2=-x^2+c^2$. Since the curve passes through $(a,b)$, it follows that $$c^2=y(a)^2+a^2=b^2+a^2.$$

Pedro
  • 18,817
  • 7
  • 65
  • 127
6

In my opinion Euclid's proof in the Elements, I. 47, is the most brilliant and elegant proof of the pythagorean theorem. One just has to look at the figure to see the WHY of the theorem...the rest is filling in the details. It is just as beautiful and as fresh, and as compelling today, as it was in 300 B.C. (more or less) when Euclid created it.

All mathematicians should see and study the proof at least once in their lives...it is a priceless jewel of mathematical beauty.

mark villarino
  • 1
2

Richard Schwartz has a nice Java applet demonstrating a proof by rearrangement of the Pythagorean theorem which is a variation on the one that you like. He constructed a wood model demonstrating this proof, with triangles that swivel.

Agol
  • 929
  • 6
  • 13
1

http://www.math.ntnu.no/~hanche/pythagoras/

1

Not a proof in itself, but the book The Pythagorean Proposition by Loomis has probably the most comprehensive collection of proofs of the Pythagorean theorem.

Lucky
  • 1,149
1

This one is probably already included here.

But just for the image...

enter image description here

johannesvalks
  • 6,407
1

Scroll down to the bottom and I think this is the most visual friendly proof in existence, there is even a gif somewhere that covers all possible cases continuously.

The first proof you mentioned however is my favorite proof of the Pythagorean theorem.

StudentofEuler2718
  • 486