Maybe enough so to explain it to children.
-
7Related: Pythagorean Theorem Proof Without Words (request for words) and What is the most elegant proof of the Pythagorean theorem? – Zev Chonoles Oct 26 '13 at 15:51
-
Any explanation of the Pythagorean Theorem that can be understood by children cannot be called a ‘proof’ in the strictest sense of the word. It is at best a ‘demonstration’. – Berrick Caleb Fillmore Oct 27 '13 at 03:45
9 Answers
I wouldn't call this a proof, but it's a convincing argument good demonstration of what the theorem means, and I thought it was pretty cool. Hopefully should help with explaining it to kids, as you asked.

-
6
-
39I don't see how it's even a convincing argument. It just shows that for this particular triangle, it happens to be true that $a^2 + b^2 = c^2$. It doesn't show why it's true, and it doesn't give us any reason why it would be true for other triangle. – Keshav Srinivasan Oct 26 '13 at 17:32
-
5I can easily imagine an animated gif like this showing that $a^2 + b^2$ is less than or greater than $c^2$. – Keshav Srinivasan Oct 26 '13 at 17:34
-
1@KeshavSrinivasan moreover it's easy to create a contraption like that in real life that proves $a^2+b^2$ is greater or less than $c^2$ by adjusting the depth – ratchet freak Oct 26 '13 at 17:50
-
9@KeshavSrinivasan resize the gif; the proof will quickly follow with the help of some fairly trivial theorems from linear algebra – Christian Chapman Oct 26 '13 at 18:26
-
1@Keshav, I agree with you completely. How can nsanger call this a convincing argument, when it's not even an argument? – TonyK Oct 26 '13 at 22:23
-
1@enthdegree: You missed Keshav's point. If the big square is thicker (in the z-dimension, if you like) than the small squares, then the water won't fill it. Likewise, if the big square is thinner, then the water will overflow. – TonyK Oct 26 '13 at 22:29
-
@enthdegree Can you elaborate on this? How should the gif be resized, and what theorems of linear algebra are you referring to? – Keshav Srinivasan Oct 27 '13 at 00:06
-
1I apologize for using the word "argument", perhaps a better phrasing would have been "demonstration of what the theorem means." The OP was asking for something that could help explain the theorem to children, so I posted a gif that I thought would help accomplish that. The post was written in 20 seconds -- it wasn't something I put a lot of thought into, so please don't look too deeply into it. – Oct 27 '13 at 00:10
-
@TonyK I wasn't talking about the thickness of the squares. I was just saying that, if you didn't already know that the Pythagorean theorem was true, there's no reason to believe that the water in the two upper squares is going to match the space in the lower square. So if you just saw this animation, you might think this was just some kind of random coincidence for this particular triangle, and you can just as we'll imagine another right triangle for which $a^2 + b^2$ is less than or greater than $c^2$. – Keshav Srinivasan Oct 27 '13 at 00:11
-
1I don't understand how this demonstration works. How come the $c$ square ends up completely full? Since it's not completely lined up with the ground, shouldn't gravity cause some of its fluid to backwash into the $a$ square? It seems like some sleight-of-hand must be going on . . . – ruakh Oct 27 '13 at 04:16
'Picture proofs' are particularly elegant. I like this one:
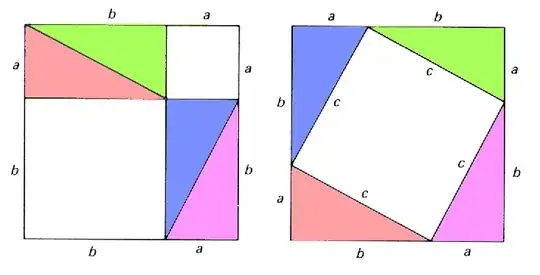
- 741
-
6this one seems to be the best as it avoid the use of formula of area of a triangle. Only requirement is the formula for area of square. – Paramanand Singh Oct 26 '13 at 16:47
-
@ParamanandSingh You don't need the formula for the area of a square. You can see from this that the area of a square of side $c$ is the same as the sum of the areas of squares of sides $b$ and $a$, you don't need to calculate those areas. – Jack M Oct 26 '13 at 21:33
-
Hm, this argument seems to rely on the area-preserving nature of rotations and translations. Is that trivial? (I'm being sarcastic.) What is trivial or non-trivial depends on one's axioms. Maybe my axioms take the area formula for a square as primitive. – Jesse Madnick Oct 27 '13 at 01:12
-
Fully agree with Jesse Madnick. And Jack M. you do need the area of a square of side $a$ as $a^{2}$. Normally this can be taken as an axiom or we can define the area of unit square as $1$ and then derive this formula by properties of addition of areas. – Paramanand Singh Oct 27 '13 at 05:00
-
You also need to prove that in the figure on the right the large white area is a square. It's obvious that all its sides have the length $c$, but are the angles right angles? – pts Oct 27 '13 at 06:59
-
1@pts That's not a big problem, since the second figure has rotational symmetry. – Tynam Oct 27 '13 at 08:41
-
@ParamanandSingh Oh, I see, you're seeing the pythagorean theorem as stating $a^2+b^2=c^2$. I would just directly state it as "sum of areas of squares equals big area". – Jack M Oct 27 '13 at 09:06
Every time you walk on a floor that is tiled like this, you are walking on a proof of the Pythagorean theorem.
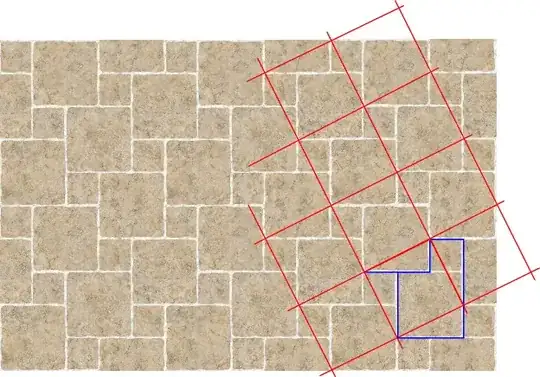 EDIT: Due to popular demand, I have added the grid in red on the right, with some triangle legs in blue.
EDIT: Due to popular demand, I have added the grid in red on the right, with some triangle legs in blue.
If you consider say the upper left corner of every small square, you can see that these points lie on a slightly diagonal periodic grid.
Each square in this grid is $c \times c$.
Then you can choose either of two easy proofs:
(1) The $c \times c$ square is clearly a rearrangement of one $b \times b$ square and one $a \times a$ square.
or
(2) Each period of the periodic pattern covers what area of floor? On the one hand there is one $a \times a$ square and one $b \times b$ square per period, while on the other hand there is one $c \times c$ square per period.
(The second proof is my favorite, since unlike most proofs it requires neither dissection nor algebra. Once you see that the tiling's periodicity is $c \times c$, you are done!)
- 9,223
-
7A picture that proves Pythagoras but contains no obvious triangle simply doesn't feel right for me :D . – us2012 Oct 26 '13 at 23:21
-
1If you are allowed to draw on the floor, you can draw the $c \times c$ grid. You will see the relevant triangle all over the place. If you are not allowed to draw on the floor, you will have to visualize the hypotenuses on your own. That is the fun part. The triangles are there. – Matt Oct 27 '13 at 19:17
-
1I have drawn some lines on the floor now so that you can see the triangles more easily. But I still recommend practicing seeing the triangles in your head even when they are not marked, so that you can enjoy the proof embedded in such floors whenever you walk on them. – Matt Nov 05 '13 at 13:29
-
This is great. I think it would be even better if the lengths were chosen so that
bis not2 a; e.g. lengths 1 and 3 instead of 1 and 2. That would have prevented my initial confusion due to the two little triangles being identical, leading to me regrouping them what turned out to be the less helpful of the two possible ways. – Don Hatch Oct 14 '20 at 19:47 -
@DonHatch I agree, it was just the first such picture I found. A picture "in general position" would of course be better. Also, I find it easiest to see the CxC grid in terms of the small squares being the grid points. This way the CxC grid is actually visually recognizable as a grid (without drawing lines on the floor). Placing the red grid this way (with grid points at the centers of the small squares) results in more tile shards but it is more symmetric, and a bunch of little triangle equivalences of the type you spotted are sufficient to fix the corners of the big square. – Matt Oct 14 '20 at 21:15
-
I see what you're saying; yes, that's now my favorite way of looking at it. Oh wait-- actually, try putting the grid points in the the centers of the large squares. Very few pieces, and no ambiguity on how to put them back together! The little square doesn't even need to be carved up. Now this is my favorite way of looking at it :-) – Don Hatch Oct 15 '20 at 00:59
For geometric proof using rearrangment there are few quite good example on the Wikipedia page. A beginner likely will not understand this quite well, because all those triangles in the picture can be confusing, so I recommend to start first with this "counting proof"
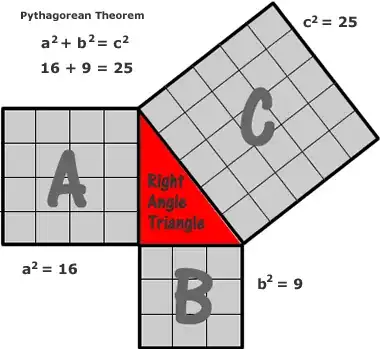
Then introduce the rearrangment pictures and animations, and at last introduce the actual formula $a^2 + b^2 = c^2$. It would be nice to lead them and help them to derive the formula by themselves, rather than just writing it on a board.
- 3,955
- 35,843
-
1I would consider this to be more of a demonstration than a proof. Such demonstrations would be undermined if the student has seen disappearing square puzzles. – Simon Oct 27 '13 at 09:22
-
1Also, how do you know that with squares of those sizes you end up with a right angle between A and B (without already knowing the pythagorean theorem)? – Mitch Oct 27 '15 at 17:43
You can cut up a square of sides $a+b$ into $a^2$, $b^2$ and four triangles of sides $a,b,c$.
You can also cut up the same square into a square of side $c$, and the same four triangles.
- 50,853
Consider the right figure and ignore the left one!

The area of the square of side $a+b$ is \begin{align*} (a+b)(a+b) &= a^2 + ab + ab + b^2\\ &= a^2 + 2ab + b^2 \end{align*}
It is equal to the sum of 4 triangles and 1 square. This sum is \begin{gather*} 4\times \frac{ab}{2} + c^2\\ 2ab+ c^2 \end{gather*}
By equating both, we have
\begin{align*} a^2 + 2ab + b^2 &= 2ab +c^2\\ a^2+b^2=c^2 \end{align*}
Now consider a single triangle so you have proven that $a^2+b^2=c^2$. Done!
- 3,896
-
1This relies on loads of non-trivial facts about area. You've got to know that the area of a rectangle is the product of its sides, and then you've got to consider that those sides might be real numbers, so you've got to know how to do arithmetic with real numbers. – Jack M Oct 27 '13 at 00:44
-
7"You've got to know that the area of a rectangle is the product of its sides." That's a non-trivial fact? That's practically my definition of area. – Jesse Madnick Oct 27 '13 at 01:06
-
1@JackM Euclid proved that area is length times width, and he did it without assuming anything about the arithmetic of real numbers. See my comment to you here: http://math.stackexchange.com/questions/803/what-is-the-most-elegant-proof-of-the-pythagorean-theorem/10867#comment1152889_10867 He did, however, use Eudoxus' theory of proportions, which basically says that two ratios are equal if and only if the same rational numbers are less than, greater than, or equal to them, so there is a reliance on something equivalent to our modern idea of real numbers, but not the arithmetic of real numbers. – Keshav Srinivasan Oct 27 '13 at 02:04
-
@JesseMadnick Not mine. I define area using a unit shape (like a square with a side of unit length) and counting the number of that shape you'd need to cover the shape whose area you'd want to measure. – Jack M Oct 27 '13 at 02:13
-
@JackM: Right, so by that definition, isn't the area of a rectangle equal to its length times its width, then? After, say, a 1-line argument? – Jesse Madnick Oct 27 '13 at 02:24
-
-
-
@JesseMadnick The point is that I'm not being pedantically formal, I'm just being practical. I'm thinking about how you would convince a hypothetical complete layman. Someone totally uninitiated wouldn't understand the motiviation behind a definition like "the area of a rectangle is the product of its sides", or that you can multiply lengths that aren't ratioanl numbers, but they would agree that (my definition of) area is invariant under rotation. – Jack M Oct 27 '13 at 09:04
-
@JackM Euclid's proof of the area of a rectangle doesn't involve the notion of multiplying irrational numbers at all. – Keshav Srinivasan Oct 27 '13 at 13:13
-
@JackM I found a proposition of Euclid that seems to demonstrate even more directly that area = length times width: http://aleph0.clarku.edu/~djoyce/java/elements/bookVI/propVI1.html – Keshav Srinivasan Nov 16 '13 at 17:03
I think that one of the simplest proofs is that attributed to US President James Abram Garfield.
The Cut the Knot page on the Pythagorean lists it as Proof #5.
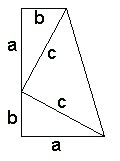
This proof, discovered by President J. A. Garfield in 1876 [Pappas], is a variation on the previous one. But this time we draw no squares at all. The key now is the formula for the area of a trapezoid - half sum of the bases times the altitude - $(a + b)/2·(a + b)$. Looking at the picture another way, this also can be computed as the sum of areas of the three triangles - $ab/2 + ab/2 + c·c/2$. As before, simplifications yield a² + b² = c².
For more of this story, see: A Mathematician for President, Let's Play Math.
PS
I just noticed that this proof was already given as an answer. I'll leave my response here as it contains more details.
PPS
My next favourite proof is probably the one based on a construction of similar triangles (Proofs #6 and #7). I think it cuts to the heart of the idea as seen by Euclid.
Then probably the simple picture proofs #3, #4, #9 - the latter already being posted as an answer to this question.
The original Euclidean proof constructed from the "Bride's Chair" always seemed a little convoluted to me.
What I will say will be the worst in terms of beauty but you need to ask yourself what is a square triangle. How is it defined ?
Well, the answer is that 2 vectors are square when their scalar product is 0, which leads (after 1 or 2 lines) to the Pythagore Theorem
Edit :
Vectors are A and B ; C = A - B to "complete the triangle"
In the general case, ||C||2 = (A-B).(A-B) = ||A||2 + ||B||2 - 2 A.B
We see that ||C||2 = ||A||2 + ||B||2 if and only if A.B == 0 (i.e are square by definition of being square)
- 1,124
-
-
-
In other words, don't explain Pythagore's formula with the area of the squares around the triangle. It does not make any sense. The formula says that the length of a "shortcut" is derived from the length of 2 legs of a path, it has nothing to do with areas – Thomas Oct 27 '13 at 10:09