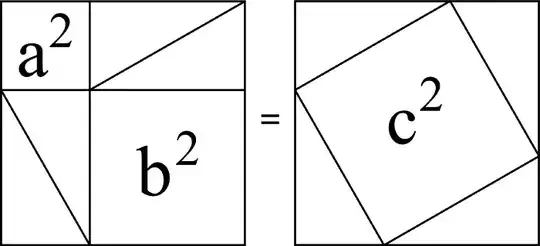
Pythagorean Theorem Proof Without Words (request for words)

Question

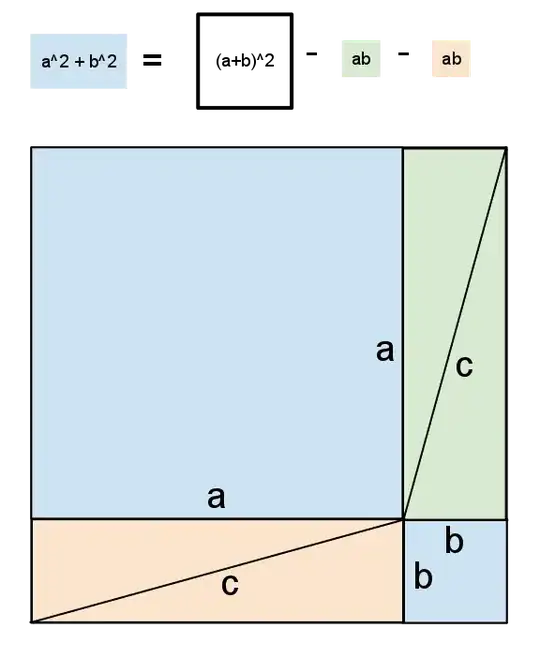
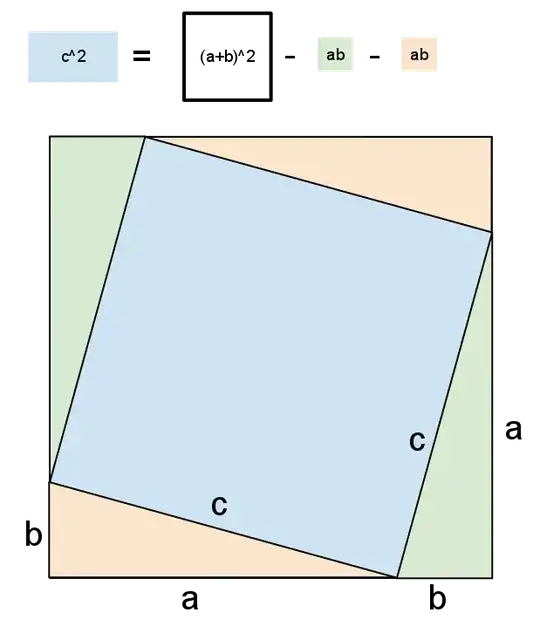
I was intrigued by a book I saw called Proofs without Words. So I bought it, and discovered that the entire book doesn't have any words in it. I figured at least it would have some words explaining the pictures or something to help understand the proofs. I was wrong.

The book gives several picture proofs of the Pythagorean theorem. Attached is the first one. Can someone add a few words (or even just arrows and labels or anything) which would help me understand how this pic proves the theorem (which says, as I know all of you know, that $a^2+b^2=c^2$, where $a$ and $b$ are the lengths of the perpendicular sides of a right triangle, and $c$ is the length of the hypotenuse).

$\qquad\quad$ enter image description here

One of Edward Tufte's books has a discussion of a Pythagorean theorem picture proof like the one above but with words. — Adam Wuerl, Jan 30 '12 at 01:39
Aside: From this Cut The Knot page: "Below is a collection of 956 approaches to proving the theorem. Many of the proofs are accompanied by interactive Java illustrations." — Pierre-Yves Gaillard, Jan 30 '12 at 08:10

score 70 · Accepted Answer · answered Jan 29 '12 at 23:26

70

How about just three letters?

$\;\;$ pythag

(Hat tip: Clipart Etc.)

answered Jan 29 '12 at 23:26

anon

151,657

1

Oh, this is nice. – Mark Beadles Jan 29 '12 at 23:28
Nice succinct answer. Frankly, the original proof I posted would have been just as wordless, but better with just those labels.
But I think we still need to prove that the four triangles in the left are congruent to the four on the right. They sure look congruent. But I don't think a geometry teacher would accept that answer. How do you prove that part?
– Jeff Jan 30 '12 at 00:19
2

@Jeff: What do you mean congruent? They're all the same triangle with sides $a$ and $b$, hypotenuse $c$ (these are actually the givens and the $a^2,b^2,c^2$ as areas are derived from these givens). – anon Jan 30 '12 at 00:24
IOW, How do you know that the ones in the left are the same triangles as the ones in the right? The ones on the right could be triangles which are really close the the ones on the left, they certainly look like the same triangles, but how do we know that they are the same (short of cutting up a piece of paper and sliding the triangles around). – Jeff Jan 30 '12 at 00:34
9

@Jeff: Because they're defined that way. Those are the givens: the fact that we construct both figures with the same triangle is our starting set of information, from which we derive the areas of the squares as $a^2,b^2,c^2$, and from there we derive $a^2+b^2=c^2$. – anon Jan 30 '12 at 00:38
4

Ohhhhhh. I see. Since the triangles are the same on both sides, the white area must be the same. Thanks. – Jeff Jan 30 '12 at 01:07
Brilliant. Nice answer. – rcollyer Jan 30 '12 at 02:10
2

you could also just symbolically tell the reader that the dimensions of the triangles are the same.... IIRC from math this is how that is done? http://i.stack.imgur.com/Iaae8.png – rlemon Jan 30 '12 at 02:11
What an amazing proof. – Xonatron Jan 30 '12 at 14:58
8

If it's really a proof, then it should make use of the parallel postulate, and it should fail if the parallel postulate fails. Presumably this assumption is hidden somewhere in the (lack of an) argument. I suppose that if the parallel postulate fails, we don't have squares with four right angles, and therefore you can't assemble things as shown. – Feb 02 '12 at 04:41

score 6 · Answer 2 · answered Jan 29 '12 at 23:29

6

The light gray and dark gray triangles are all copies of the same right triangle.

The outline of each figure is a square with side length $a+b$; in particular their area is the same. Because both figures contain 4 gray triangles (even in the same orientations on both sides), the total area of the white portions must be the same on both sides. On the left, the white consists of one square of area $a^2$ and another square of area $b^2$. On the right, the white consists of a single square of area $c^2$. Since the total area is the same, we must have $a^2+b^2=c^2$.

answered Jan 29 '12 at 23:29

hmakholm left over Monica

286,031

Good explanation. But I think we still need to prove that the triangles on the left are congruent to the triangles on the right. How? – Jeff Jan 30 '12 at 00:19
I think the point is that its up to you to imagine this is possible - then verify that it is true by creating (as a given) the model on the right with triangles that are congruent to the ones of the model on the left side. (Then you should confirm that the quadrilateral in the center is a square, just to be thorough about it!) – Jim Jan 30 '12 at 16:30

score 4 · Answer 3 · answered Jan 29 '12 at 23:28

Call "a" the short leg of any of the shaded triangles above, and "b" the long leg. Call "c" the hypotenuse.

In the figure on the left, we see two small white squares within the larger square: one small square has sides equal to "a". The other has sides equal to "b". So the area in white on the left is $a^2 + b^2$.

In the figure on the right, we have rearranged the same 4 triangles to new positions with a larger square congruent to the first one. This time we see one white square. Its sides are equal to "c", the hypotenuse. So its area is $c^2$.

The area in white in both triangles must be equal, since all we have done is rearrange the triangles. Since the white areas are equal, $a^2+b^2=c^2$ QED.

Thanks Mark. I have the same issue with this proof as with the last Henning's: We still need to prove that the triangles on the left are congruent to the ones on the right (don't we?). — Jeff, Jan 30 '12 at 00:19

score 4 · Answer 4 · edited Mar 16 '14 at 14:22

4

This is a simple way to split a big square (depicted by the large colorless square in the equation) into the smaller green and orange right triangles and blue squares (depicted by colored shapes in the equation)

After moving around the right triangles as in this figure, the two smaller blue squares in earlier picture become a bigger one here. Since the sizes of none of the non-blue shapes have been changed, the blue shapes must certainly add up to the same area (as depicted by the equation)

edited Mar 16 '14 at 14:22

Guy

8,857
1
28
57

answered Jan 30 '12 at 07:11

hyperbolic

41

3

incidentally as an aside, and this is perhaps way too obvious, the first picture in the picture proof also demonstrates the equality $(a+b)^2 = a^2 + b^2 + 2ab$. – hyperbolic Jan 30 '12 at 07:28

score 3 · Answer 5 · answered Jan 29 '12 at 23:30

3

first pic: 4 triangles and 2 squares (with sides $a$ and $b$)

second pic: same 4 triangles and 1 square with sides equal to $c$

total area of of the 2 big squares are the same

so sum of the areas of the 4 triangles plus the areas of the 2 small squares ($a^2+b^2$) is equal to the sum of the areas of the 4 triangles plus the area of the 1 big square ($c^2$)

answered Jan 29 '12 at 23:30

ratchet freak

1,930

same 4 triangles How do you konw they're the same 4 triangles? – Jeff Jan 30 '12 at 00:18
congruent triangles at least there's a right angle and the respective adjoining it sides are equal lengths – ratchet freak Jan 30 '12 at 00:30

score 0 · Answer 6 · answered Jan 09 '14 at 09:07

0

enter image description here

Gravity goes this $\longrightarrow$ way. Turn your screen ;-)

answered Jan 09 '14 at 09:07

draks ...

18,449

5

That's cute, but not really an answer to this question. – hmakholm left over Monica Jan 09 '14 at 10:45
What does this refer to? – Jeff Jan 10 '14 at 00:43
@jeff do you recognize $a^2,b^2$ and $c^2$ in the figure? It's actually the same is in the accepted answer...Do you think it doesn't fit to your question as well? – draks ... Jan 10 '14 at 11:19
I didn't notice the figure the first time. I read the text only. Pretty cool graphic, actually. – Jeff Jan 16 '14 at 04:48
Larger version, correctly oriented, available in this post. But it isn't a proof, and it certainly isn't an answer to the question at hand. – MvG Apr 22 '14 at 14:49

Pythagorean Theorem Proof Without Words (request for words)

6 Answers6

Linked