13

To me, it seems that the Pythagorean theorem is a special case of the law of cosines. However, all derivations that I can find seem to use the Pythagorean theorem in the derivation. Are there any simple (preferably geometric) derivations of the law of cosines that don't reference the Pythagorean theorem?

Martin Sleziak
  • 53,687
Nate
  • 2,205
  • I think any proof of Pythagoras theorem can be adapted to get the law of cosines. –  May 21 '12 at 06:21
  • 1
    You might have already looked at this. But wiki has some nice collections including a proof comparing the areas of a heptagon. (http://en.wikipedia.org/wiki/Law_of_cosines#By_comparing_areas) –  May 21 '12 at 06:34
  • See my answer to "What is the most elegant proof of the Pythagorean Theorem?" : http://math.stackexchange.com/a/1336/409 – Blue May 21 '12 at 06:35
  • Beautiful. Could you post it here so I can credit the answer? – Nate May 21 '12 at 09:51
  • 1
    The law of cosines and Pythagoras theorem are equivalent. – lhf May 21 '12 at 10:39

2 Answers2

19

[As requested, posting a comment as a full answer.]

Taken from my answer to the question "What is the most elegant proof of the Pythagorean Theorem?" ...

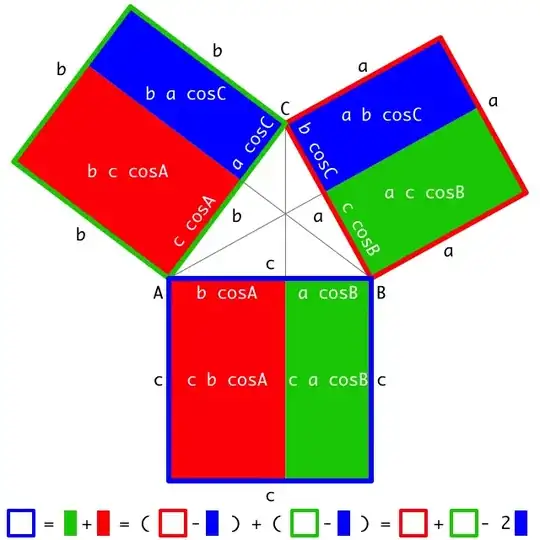
Law of Cosines Picture Proof

Community
  • 1
Blue
  • 75,673
  • 2
    What's fun is if C is in fact a right angle, the blue rectangles shrink to nothing, and you're left with Euclid's proof of Pythagoras. He was so close to proving it all in one go! – coolpapa Sep 09 '22 at 22:59
1

Nothing comes to mind. There are a few ways of saying that the Law of Cosines as you know it demands the Pythagorean Theorem. Your questions appear to be about simplifying mathematics, as mentioned on your website. It turns out that there is always an irreducible minimum that needs to be taken more or less on faith. In the setting of plane geometry, one of these items is the Parallel Postulate. With that and the other axiomatic items, the Law of Cosines is true.

On the other hand, if you prefer to deny the parallel postulate, you get the hyperbolic plane (actually there is a constant involved) where there are two unfamiliar Laws of Cosines, because similar triangles are always congruent. Not my fault, I just work there.

I suggest you get Geometry: Euclid and Beyond by Hartshorne and Euclidean and Non-Euclidean Geometries, 4th edition, by Greenberg.

Will Jagy
  • 139,541
  • 2
    I don't buy it. The Pythagorean Theorem is a special case of the law of cosines. I won't believe that there's not a proof of the latter (independent of the former) until I see a proof that it can't be done. – Nate May 21 '12 at 09:31
  • Alright. I will leave this here, although there is an answer now that seems to be what you actually wanted. – Will Jagy May 21 '12 at 19:44