Beautiful, simple proofs worthy of writing on this beautiful glass door

Question

What are some of the more beautiful proofs you know? I am measuring beauty in two dimensions -- first, how conceptually elegant is it and second, how aesthetically pleasing is it.

Context: I work at a econ consulting firm. We're mostly math majors or very quantitative econ majors. A buddy and I are trying to decide what to write on the glass door to the office we share. Currently it has a graph of quality of Brad Pitt's movies against how frequently he was shirtless in that movie. Time to upgrade that...

Answer 1

Barak beat me to my #1 choice. This would be second:

Answer 2

$\qquad\qquad\qquad\qquad$

$\qquad\qquad\qquad\qquad\quad$ Geometric Explanation of the Binomial Theorem

---

$\qquad\qquad\qquad\qquad\qquad\qquad\quad$

$\qquad\qquad\qquad\qquad\qquad\qquad\qquad$ Proof that $~\displaystyle\sum_{k=1}^n(2k-1)=n^2$

Answer 3

Cosines and Sines Around the Unit Circle

Trigonometric Angle Sum and Difference

Answer 4

For me, it's Conway's inverse proof of the Morley equilateral triangle:

Answer 5

I tried to find problems from different areas. My five suggestions are.

Sophomore' dream. The formula for the problem is: $$\begin{align}\int_0^1 x^{-x}\,dx &= \sum_{n=1}^\infty n^{-n}\end{align}$$ You can find facts about the problem and the proof of it at Sophomore's dream wikipedia article.

Bretschneider's formula. This is an expression for the area of a general convex quadrilateral. $$K = \sqrt {(s-a)(s-b)(s-c)(s-d) - abcd \cdot \cos^2 \left(\frac{\alpha + \gamma}{2}\right)}$$ It is the generalization of Brahmagupta theorem and Henon's formula. You can find the proof at Bretschneider's formula wiki article.

Feuerbach's circle. It is a circle that can be constructed for any given triangle.

It is also named nine-point circle because it passes through nine significant concyclic points defined from the triangle. Find more at Nine-point circle wiki article.

Taxicab numbers. If you want a funny story and numbers on the door.

I remember once going to see him when he was lying ill at Putney. I had ridden in taxi-cab No. 1729, and remarked that the number seemed to be rather a dull one, and that I hoped it was not an unfavourable omen. "No", he replied, "it is a very interesting number; it is the smallest number expressible as the sum of two [positive] cubes in two different ways.

$$1729 = 1^3 + 12^3 = 9^3 + 10^3$$ More details about the story and list of numbers at Taxicab number and 1729 wiki articles. Also Ramanujan's wikipedia page could be interesting.

Monty Hall problem. Or a door-within-doors.

Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice?

More details at Monty Hall problem wikipage.

Answer 6

I'm fond of Euclid's proof of the infinitude of primes: For any finite set $S=\{p_1, p_2,\dots, p_k\}$ of prime numbers, let $N=p_1\cdot p_2\cdot\cdots\cdot p_k+1$. Then $N$ isn't divisible by any prime in $S$. Hence it is divisible by some other prime. Hence the set $S$ does not include all primes. Thus there must be infinitely many primes.

Answer 7

Proof of Euler's Identity: $$e^{\pi{i}}+1=0$$

BTW, your question is more or less a copy of "Simple" beautiful math proof, so you might wanna check it out too. There's some great colorful stuff there, my answer being somewhere in the middle.

Answer 8

Here are a few visual proofs that

$$\text{arctan}(1) + \text{arctan}(2) + \text{arctan}(3) = \pi$$

One by user KennyTM:

---

More by user dldarek:

---

I think the lattice nature of the proofs would look nice on a door.

Answer 9

Some suggestions:

$1$. The proof for the Gaussian integral

$$\int_{-\infty}^{\infty}e^{-x^2} \mathrm dx=\sqrt{\pi}$$

$2$. The proof for Euler's solution to the Basel problem

$$\frac {\ \ \pi^2}6=\sum_{n=1}^{\infty}\frac 1{n^2}=\frac 1{1^2}+\frac 1{2^2}+\frac 1{3^2}+\frac 1{4^2}+\cdots+\frac 1{n^2}+\cdots$$

$3$. The proof for Wallis' product $$\frac \pi 2=\frac 21 \cdot \frac 23\cdot \frac43\cdot\frac45\cdot\frac65\cdot\frac67\cdots $$

From the above it is interesting to note how $\pi^{\frac 12}$, $\pi$ and $\pi^2$ can be computed using an integral, an infinite product, and an infinite sum respectively.

Perhaps something more relevant for a glass door would the equations written on the glass window by John Nash (Russell Crowe) in the movie "A Beautiful Mind"!

Answer 10

The rudimentary differential equation proof of Euler's formula in the complex plane $e^{i \pi}=-1$, where $i=\sqrt{-1}$. First, via $\frac{d}{d\theta}$,

$$e^{i\theta}=f(\theta)+ig(\theta) \implies ie^{i\theta}=f^{\prime}(\theta)+ig^{\prime}(\theta)=if(\theta)-g(\theta).$$

Comparing real and imaginary parts, $f(\theta)=g^{\prime}(\theta)$ and $f^{\prime}(\theta)=-g(\theta)$ which implies

$$f^{\prime \prime}(\theta)+f(\theta)=0 \implies f(\theta)=\cos(\theta),\: g(\theta)=\sin(\theta).$$

Evaluating at $\theta=\pi$, gives $e^{i\pi}=-1$.

Answer 11

The proof for the irrationality of $\sqrt{2}$ is pretty simple and satisfying, I think. It's a very easy result to achieve, but the proof is very elegant and has some nice symmetry.

Assume $\sqrt{2} = \frac{p}{q}$ with p and q relatively prime (totally simplified).

$2q^2 = p^2$

$p^2$ is even

the square of an odd number is odd, so $p$ must be even. Let $p=2r$

$2q^2=4r^2$

$q^2=2r^2$

$q^2$ is even

the square of an odd number is odd, so $q$ must be even

contradiction: $p$ and $q$ are both even, so they are not relatively prime. $\sqrt{2}$ must be irrational.

Answer 12

The classification of finite simple groups -- so there would finally be a single reference that could be given for this important result. ;)

Answer 13

Calculus

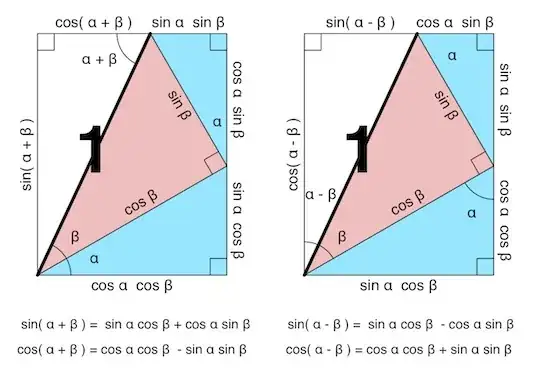
The proof that $\frac{22}{7} > \pi$.

$$ \begin {align*} 0 &< \displaystyle\int_0^1 \frac {x^4 \left( 1 - x \right)^4}{1 + x^2} \, \mathrm{d}x \\&= \displaystyle\int_0^1 \frac {x^4 - 4x^5 + 6x^6 - 4x^7 + x^8}{1 + x^2} \, \mathrm{d}x \\&= \frac {22}{7} - \pi. \end {align*} $$

Geometry

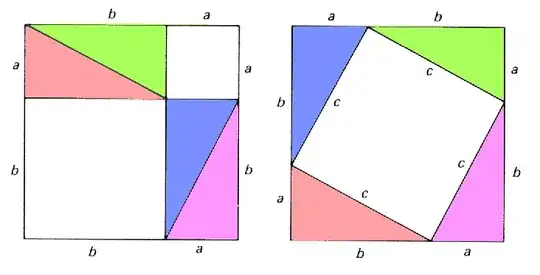
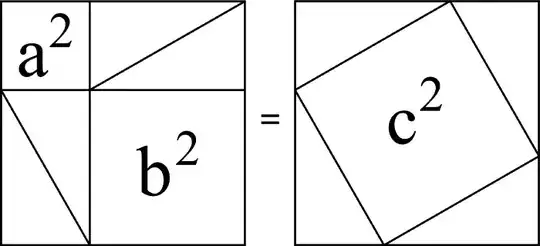
The Pythagorean Theorem.

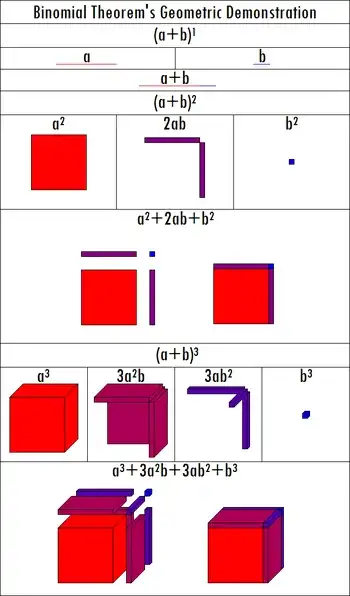
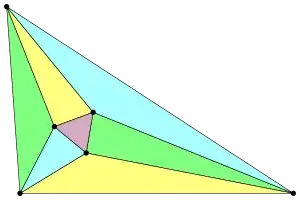
Algebra

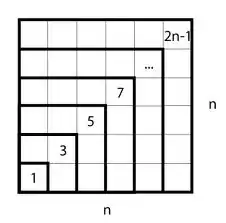
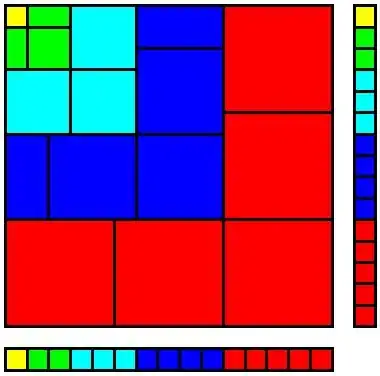
Proof that $ \displaystyle\sum_{k=1}^{n} k^3 = \left( \displaystyle\sum_{k=1}^{n} k \right)^2 $: a proof without words.

Number Theory

1. Deriving Binet's Formula.
2. Finding two irrationals $x,y$ such that $x^y$ is rational. If $x=y=\sqrt2$ is an example, then we are done; otherwise $\sqrt2^{\sqrt2}$ is irrational, in which case taking $x=\sqrt2^{\sqrt2}$ and $y=\sqrt2$ gives us: $$\left(\sqrt2^{\sqrt2}\right)^{\sqrt2}=\sqrt2^{\sqrt2\sqrt2}=\sqrt2^2=2.\qquad\square$$

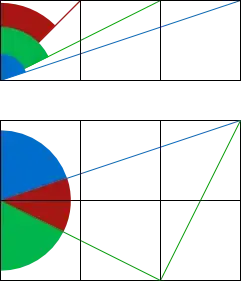
Combinatorics

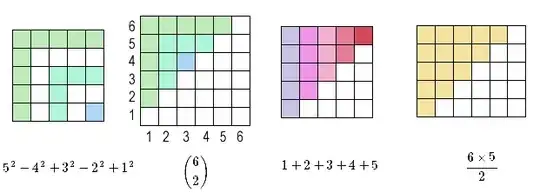
Binomial coefficients equal alternating sum of squares $-$ see leonbloy's answer.

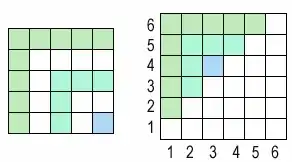
On the left, you have the alternating sum as an inclusion-exclusion of squares: the total sum is the number of coloured cells.

On the right, you have those L shaped shapes rearranged in the top left of a 6x6 grid. If you think of each cell as a coordinate $(x_1,x_2)$ that gives two elements chosen from the set $\{1, 2 \cdots 6\}$, it's seen that the elements are choosen with $ x_2 > x_1$, what corresponds to a combination (no repetition, and no order).

The others are well known, but, just for the sake of completeness...

$$\displaystyle \sum_{k=1}^n (-1)^{n-k} k^2 = {n+1 \choose 2} = \sum_{k=1}^n \; k = \frac{(n+1) \; n}{2}$$

---

As a side note, this link is excellent if you want to find your own and decide if proofs you see are actually nice.

Also, if you want to see a list of awesome proofs without words, see here.

Answer 14

A still image from the top-voted entry at https://mathoverflow.net/questions/8846/proofs-without-words along with the equation it proves, $1+2+\cdots+(n-1)={n\choose2}$, could be good. (Note: the entry there was originally just a still. Personally I find the animation a little unpleasant, but that may just be me.)

Added later: The original version of this proof without words, which appeared in "A Discrete Look at $1+2+\cdots+n$" by Loren Larson, can be found at http://www.matem.unam.mx/~rod/teaching/mac/larson-discrete_look_gauss_series.pdf (see Figure 7 there).

Answer 15

Euler's identity in matrix form (link for proof):

$$ \color{#10a}{\large{e^{i \, \mathbf{\Pi}} + \mathbf{I} = \mathbf{0}} }$$

Cheers!

Answer 16

The proof of the interpolation theorem three steps which seems redundant yields an amazing result Or the proof for the gamma function at 1/2 gives pi otherwise known as (1/2)!=π

EDIT:as noted in the comments square root of pi is actually the value of of the gammq function at 1/2 which is defined for (n-1)!