I stumbled across this relationship while I was messing around. What's the proof, and how do I understand it intuitively? It doesn't really make sense to me that the sum of odd numbers up to $2x + 1$ should equal $x^2$.
-
I believe the upper bound is supposed to be $x-1$, but yes, that is correct. I'll explain in more detail in the answer. – 2012ssohn Mar 03 '14 at 13:42
-
Consider the "consecutive difference" $(x+1)^2-x^2$. What is the result? What about for $x^2-(x-1)^2$? Note that in general this is referred to as a "finite difference" on Wikipedia, etc. – abiessu Mar 03 '14 at 13:42
-
We know that $\sum_{k=0}^x k=\frac{k(k+1)}{2}$. – Pol van Hoften Mar 03 '14 at 13:43
-
17I like the title (intended pun or not): "I found this odd relationship..." – amWhy Mar 03 '14 at 14:08
8 Answers
How do I understand it intuitively? It doesn't really make sense to me that the sum of odd numbers up to $2x+1$ should equal $x^2$
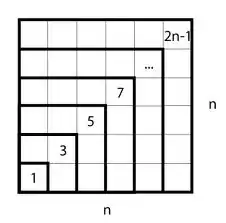
Hope this picture will provide you with the visual aid you need. :-)
- 48,334
- 2
- 83
- 154
-
6In terms of understanding "why", this is probably the best descriptor. – Simon Rose Mar 03 '14 at 14:03
-
-
1
Recall that:
$$\sum_{k=0}^{x}k = \frac{x(x+1)}{2}$$
Then
$$\sum_{k=0}^x(2k + 1) = 2\sum_{k=0}^x k + \sum_{k=0}^x1 = x(x+1) + (x+1) = x^2 + 2x + 1 \neq x^2$$
Instead, since $x^2 + 2x + 1= (x+1)^2$, then
$$\sum_{k=0}^x(2k + 1) = (x+1)^2$$
Using $x-1$ in place of $x$, then you have:
$$\sum_{k=0}^{x-1}(2k + 1) = x^2$$
- 14,064
- 4
- 35
- 62
We prove this via induction.
Base case ($x = 1$): $$1^2 = \sum_{k=0}^{1-1} (2k+1) = \sum_{k=0}^0 (2k+1) = 2\cdot 0+1 = 1$$
Inductive step: Suppose it is true for some $x$. Now, we note that $$(x+1)^2 = x^2 + 2x + 1$$
and that
$$\sum_{k=0}^{x+1-1} (2k+1) = \sum_{k=0}^{x-1} (2k+1) + 2x+1$$
- 3,827
-
1
-
4@Sabyasachi - the question asked for a proof, which I have provided. – 2012ssohn Mar 03 '14 at 13:52
Notice : $$\begin{align}(x + 1)^2 - x^2 &= x^2 + 2x + 1 - x^2 \\&= 2x + 1\end{align}$$
We take a summation on both sides and see that a lot of cancellation occurs on the LHS:
$$\sum_{k = 0}^{x-1}\left((x+1)^2 - x^2\right) = \sum_{k = 0}^{x-1}(2x+1)\\ (x -1 + 1)^2 - 0^2 = \sum_{k = 0}^{x-1}(2x+1)\\ x^2 = \sum_{k = 0}^{x-1}(2x+1)$$
- 74,685
- 14,435
The standard proof without words is as follows:
1 12 123 1234 ...
22 223 2234
333 3334
4444
- 9,432
-
what is this even supposed to mean? Not ridiculing, but you can consider adding an explanation. Doesn't look "standard" to me – Guy Mar 03 '14 at 13:49
-
@Sabyasachi: Calculate the area of the squares in two ways: side length squared is the same as what you get by going layer by layer. The number of squares in the last layer increases by $2$ at each step and is initially $1$. – J. J. Mar 03 '14 at 13:59
-
-
3@Sabyasachi: It's not traditional with proofs without words. Besides, Lucian posted the same proof with a nicer picture. – J. J. Mar 03 '14 at 14:14
-
I was just saying that your proof is brilliant and intuitively the best, but only once you make it clear what you mean by those numbers. It wasn't immediately obvious that you were drawing individual cells of a sqaure. Anyway +1 major upvote. – Guy Mar 03 '14 at 14:20
$\sum_{k=0}^{x-1}2k=\left(0+\left(x-1\right)\right)+\left(1+\left(x-2\right)\right)+\cdots+\left(\left(x-1\right)+0\right)=x\left(x-1\right)=x^{2}-x$
hence:
$\sum_{k=0}^{x-1}(2k+1)=\sum_{k=0}^{x-1}2k+x=x^2$
- 151,093
I noticed this a few days ago and verified the first 1,000,000,000 with a program. If you FOIL it, it makes sense. For example:
(4+1)(4+1) = 4x4 + 4x1 + 4x1 + 1 = 25
Obviously this is equal to 5x5. Notice that the last three terms are odd when added because
2x + 1
is consecutive odd numbers, and the first term is the previous square. If we generalize:
(X+1)(X+1) = X*X + X*1 + X*1 + 1 = X^2 + 2X + 1
Does this help?
- 11