-1

if given a positive integer $n$ is the sum of the $n$ smallest odd numbers equal to $n^2$

yeyee6512y
  • 11
  • 3
  • Base case: Prove/show/verify for $n=1$. Induction hypothesis: assume true for $n=k$. Step 3: Prove true for $n=k+1$. – paw88789 Aug 26 '14 at 23:13
  • It looks as if you want to show this: The sum of the $n$ smallest odd positive integers is equal tn^2$. Induction is one way to do it. – André Nicolas Aug 26 '14 at 23:13
  • @Andre N: Sum of $n$ smallest odd positive integers, I think. – paw88789 Aug 26 '14 at 23:15
  • Yes, forgot to write odd. You want to show that if the sum of the odds up to $2k-1$ is $k^2$, then the sum of the odds up to $2(k+1)-1$ is equal to $(k+1)^2$. This is easy, because $k^2+(2k+1)=(k+1)^2$. – André Nicolas Aug 26 '14 at 23:17
  • A few suggestions: (1) try to search before asking. Most standard induction questions have been asked and answered before. (2) Write a descriptive title for your question. This is for your own benefit: the system will suggest related posts based on title. (3) Use LaTeX. –  Aug 26 '14 at 23:25
  • I would remove the "Show that..." from the question, as it really confused me at first. I thought you were trying to find a number equal to the sum of all odd numbers less than it, and also equal to its own square. – Ryan Aug 27 '14 at 00:00

3 Answers3

6

My favorite, the proof without words:

Ahaan S. Rungta
  • 7,706
2

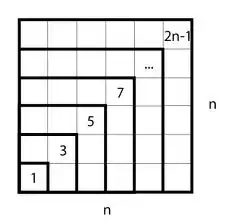
First we observe that the pattern seems to hold. $1^2 = 1, 2^2 = 1+3 , 3^2 = 1+3+5, \ldots$

Then we notice that this is: $2^2 = 1^2 + 3, 3^2=2^2 + 5, \ldots$ and we predict that: $$(n+1)^2 =\mathop{(n)^2 + \underbrace{(2(n+1)-1)}}_{\text{the }(n+1)^{th}\text{ odd number}}$$

For a proof by induction, $\require{cancel}\cancelto{\text{you}}{\text{we}}$ need to demonstrate that this is so for all positive integer $n$. (Having already established the base case: $n=1: 1^2=1$)

More formally: The steps in proof by induction are:

$$\begin{align} & \mathsf P(1) & \text{base case}\\ & \forall n\in\mathbb{Z}^+ : \mathsf P(n)\to \mathsf P(n+1) & \text{iterative case} \\ \therefore \quad & \forall n\in\mathbb{Z}^+ : \mathsf P(n) & \text{by induction}\end{align}$$

Our premise is: $\mathsf P(n):= (n^2=\sum_{k=1}^n (2n-1))$

Base case: $1^2= (2(1)-1) \quad\color{green}{\checkmark}$

Iterative case: $\Bigl(n^2 = \sum_{k=1}^n (2n-1))\implies \underbrace{(n+1)^2 = n^2 + (2(n+1)-1)}_{\text{show this is true for all }n\in\mathbb Z ^+}\Bigr) \quad \color{green}{?}$

Notes

The $k^{th}$ odd number is $2k-1$. As in: $1=2(1)-1, 3=2(2)-1, 5=2(3)-1, \ldots$.

Then the sum of the first $n$ odd numbers is: $a_n:=\sum_{k=1}^n (2k-1)$ $$\begin{align}a_n &:= 1+3+5+\cdots+(2n-1)\end{align}$$

It follows that the sum of the first $n+1$ odd numbers must be: $a_{n+1} = \sum_{k=1}^{n+1} (2k-1)$ $$\begin{align}a_{n+1}&:= 1+3+5+\cdots+(2 (n)-1)+(2 (n+1)-1)\end{align}$$

Hence by subtraction it is that: $a_{n+1} - a_{n} = (2(n+1)-1)$

Now if it is that: $a_n=(n)^2$ then it would also be that: $a_{n+1} = (n+1)^2$.

Thusly our induction step needs to show: $(n+1)^2 = (n)^2 + (2(n+1)-1)$

Graham Kemp
  • 129,094
0

You want to show $1+3+\cdots+(2n-1)=n^2$. Note that $1+2+\cdots+2n=n(2n+1)$, and $2+4+\cdots+2n=2(1+2+\cdots+n)=n(n+1)$. Can you prove these two formulas? Your result now follows by subtraction.

voldemort
  • 13,182