Proof that the sum of the first $n$ odd numbers is $n^2$.

Question

Here is what I have so far:

The $n$th odd number is $2n-1$.

So we prove that $1+3+...+(2n-3)+(2n-1)= n^2$.

Separate the last term and you get: $[1+3+...+(2n-3)]+(2n-1)$

$[1+3+...+(2n-3)]$ is the sum of the first $(n-1)$ odd numbers.

Here is where I get stuck. The textbook says that the sum of the first $(n-1)$ odd numbers is $(n-1)^2$, but why is that the case? It seems like a recursive explanation because we are trying to prove that the sum of the first $n$ odd numbers is $n^2$. Since we have not yet proved that, how can one say with certainty that the sum of the first $(n-1)$ odd numbers is $(n-1)^2$ ?

Answer 1

Here is a proof without words:

Answer 2

Assume that the statement is not true.

Then a smallest odd number $2n-1$ must exist with $1+\cdots+(2n-1)\neq n^2$.

Based on $2\cdot1-1=1^2$ we conclude that $n>1$.

However, then we find: $$1+\cdots+(2n-3)+(2n-1)=(n-1)^2+(2n-1)=n^2$$

That means that we found a contradiction and our conclusion is that our assumption (i.e. "the statement is not true") must be incorrect.

Final conclusion: the statement is true.

Answer 3

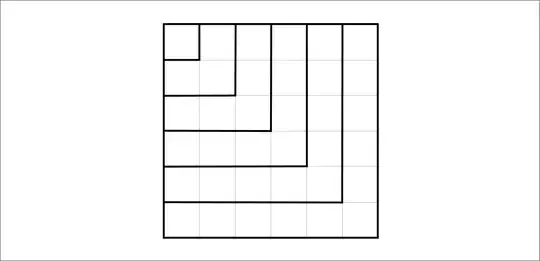
Another way of looking at is ...

$$\begin{align}&1 + 3 + 5 + {\dots} + 2n - 1 \\ &= (n - (n - 1)) + {\dots} + (n - 4) + (n - 2) + n + (n + 2) + (n + 4) + {\dots} + (n + n - 1)\\ &= n + n +n + {\dots} +n (n times)\\ &= n^{2}\end{align}$$

It can also be proved with the sum of arithmetic progression. The sum of an $A.P.$ with $n$ terms, difference $d$, and initial term $a$.

$$\begin{align}T_1 &=a\\ T_2 &=a + 2d\\ .\\ .\\ .\\ T_n &= a + (n-1)d\end{align}$$

Adding all these terms,

$$\begin{align}S &= na + d(1+2+{\dots}+n-1)\\ S &= na + \frac{n(n-1)d}{2}\\ S &= \frac{n}{2}(a + a + (n-1)d)\\ S &= \frac{n}{2}(a + T_n)\end{align}$$

Applying this to our series,

$$\begin{align}S &= \frac{n}{2}(1+2n - 1)\\ S &= n^{2}\end{align}$$

This property of odd numbers was used to generate Pythagorean triplets by Fibonacci. $1$. Pick an odd number and square it. The number chosen in $m$.

$2$. $m^2$ also lies in the series. Take the sum of all odd numbers before $m^2$. It is $(\frac{(m^2-1)}{2})^2$

$3$. Adding these two numbers will also be a perfect square. $m^2 +(\frac{m^2-1}{2})^2 = \frac{m^4 +2m^2+ 1}{4} = (\frac{m^2 + 1}{2})^2$

The numbers, $m, \frac{m^2-1}{2}, \frac{m^2+1}{2}$ are a Pythagorean triplet, wherever m is odd.

Answer 4

The proof consists of two steps:

$1.$ The basis (base case): prove that the statement holds for the first natural number $n$. Usually, $n = 0$ or $n = 1$, rarely, $n = –1$ (although not a natural number, the extension of the natural numbers to $–1$

$2.$ The inductive step: prove that, if the statement holds for some natural number $n$, then the statement holds for $n + 1$. The hypothesis in the inductive step that the statement holds for some n is called the induction hypothesis (or inductive hypothesis). To perform the inductive step, one assumes the induction hypothesis and then uses this assumption to prove the statement for $n + 1$.

Whether $n = 0$ or $n = 1$ depends on the definition of the natural numbers. If $0$ is considered a natural number, as is common in the fields of combinatorics and mathematical logic, the base case is given by $n = 0$. If, on the other hand, $1$ is taken as the first natural number, then the base case is given by $n = 1$.

Answer 5

Hint:

If you want justify the inductive assumption than note that the sum $$ 1+3+5+\cdots +(2n-5)+(2n-3)+(2n-1) $$ can be reordered as $$ (1+(2n-1))+(3+(2n-3))+(5+(2n-5)) \cdots= 2n +2n +\cdots $$ and counts the number of the $2n$ terms in the final sum ( with a bit of care when $n$ is odd).

Answer 6

We have $$\sum_{i=1}^n 2i-1 = 2\sum_{i=1}^n i - n = n(n+1) - n = n^2 $$

Edit: To respond to your point, the textbook is using something known as "mathematical induction". The idea is, simply, that you are allowed to assume a particular statement is true for the case $n-1$. If the statement is true for a particular base case, and it being true for $n-1$ implies that it is true for $n$, it true for all natural numbers.

Think of it like an infinite number dominoes falling. If one domino falls, the subsequent one does as well. Hence we simply need to make the first domino fall to make every one of the dominoes fall.

Answer 7

You can solve this question simply by using the formula for an arithmetic series. the formula is n(2a+(n-1)d)/2 By simply plugging in the values you get. n(2x1+(n-1)2)/2 Now you get. n(2n-2+2)/2 Now it is 2n(n)/2 2n^2/2 = n^2 Hence Proved.