"Simple" beautiful math proof

Question

Is there a "simple" mathematical proof that is fully understandable by a 1st year university student that impressed you because it is beautiful?

Answer 1

Here's a cute and lovely theorem.

There exist two irrational numbers $x,y$ such that $x^y$ is rational.

Proof. If $x=y=\sqrt2$ is an example, then we are done; otherwise $\sqrt2^{\sqrt2}$ is irrational, in which case taking $x=\sqrt2^{\sqrt2}$ and $y=\sqrt2$ gives us: $$\left(\sqrt2^{\sqrt2}\right)^{\sqrt2}=\sqrt2^{\sqrt2\sqrt2}=\sqrt2^2=2.\qquad\square$$

(Nowadays, using the Gelfond–Schneider theorem we know that $\sqrt2^{\sqrt2}$ is irrational, and in fact transcendental. But the above proof, of course, doesn't care for that.)

Answer 2

How about the proof that

$$1^3+2^3+\cdots+n^3=\left(1+2+\cdots+n\right)^2$$

I remember being impressed by this identity and the proof can be given in a picture:

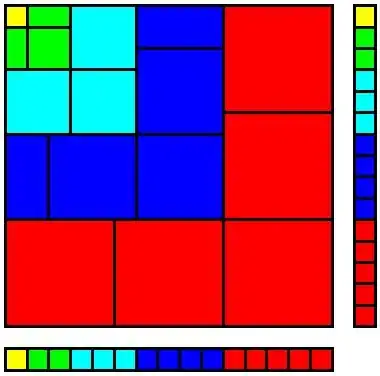
The picture is taken from Brian Sears' webpage. See also here.

Edit: Substituted $\frac{n(n+1)}{2}=1+2+\cdots+n$ in response to comments.

Answer 3

Cantor's Diagonalization Argument, proof that there are infinite sets that can't be put one to one with the set of natural numbers, is frequently cited as a beautifully simple but powerful proof. Essentially, with a list of infinite sequences, a sequence formed from taking the diagonal numbers will not be in the list.

Answer 4

Prove that if $n$ and $m$ can each be written as a sum of two perfect squares, so can their product $nm$.

Proof 1: Let $n = a^2+b^2$ and $m=c^2+d^2$ ($a, b, c, d \in\mathbb Z$). Then, there exists some $x,y\in\mathbb Z$ such that

$$x+iy = (a+ib)(c+id)$$

Taking the magnitudes of both sides are squaring gives

$$x^2+y^2 = (a^2+b^2)(c^2+d^2) = nm$$

Proof 2: With same definition, let $n = a^2+b^2$ and $m=c^2+d^2$ ($a, b, c, d \in\mathbb Z$)$$(a^2 + b^2)(c^2 + d^2) = (ac)^2 + (bd)^2 + (ad)^2 + (bc)^2$$. This can be written as $$(ac)^2 + 2abcd + (bd)^2 + (ad)^2 - 2abcd + (bc)^2$$ This can be factored and can be written as sum of two square $$(ac + bd)^2 + (ad - bc)^2$$

Answer 5

I would personally argue that the proof that $\sqrt 2$ is irrational is simple enough for a university student (probably simple enough for a high school student) and very pretty in its use of proof by contradiction!

Answer 6

I would go for the proof by contradiction of an infinite number of primes, which is fairly simple:

• Assume that there is a finite number of primes.
• Let $G$ be the set of all primes $P_1,P_2,...,P_n$.
• Compute $K = P_1 \times P_2 \times ... \times P_n + 1$.
• If $K$ is prime, then it is obviously not in $G$.
• Otherwise, none of its prime factors are in $G$.
• Conclusion: $G$ is not the set of all primes.

I think I learned that both in high-school and at 1st year, so it might be a little too simple...

Answer 7

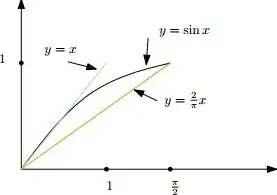
By the concavity of the $\sin$ function on the interval $\left[0,\frac{\pi}2\right]$ we deduce these inequalities: $$\frac{2}\pi x\le \sin x\le x,\quad \forall x\in\left[0,\frac\pi2\right].$$

Answer 8

The first player in Hex has a winning strategy.

There are no draws in hex, so one player must have a winning strategy. If player two has a winning strategy, player one can steal that strategy by placing the first stone in the center (additional pieces on the board never hurt your position) then using player two's strategy.

Answer 9

You cannot have two dice (with numbers $1$ to $6$) biased so that when you throw both, the sum is uniformly distributed in $\{2,3,\dots,12\}$.

For easier notation, we use the equivalent formulation "You cannot have two dice (with numbers $0$ to $5$) biased such that when you throw both, the sum is uniformly distributed in $\{0,1,\dots,10\}$."

Proof: Assume that such dice exist. Let $p_i$ be the probability that the first die gives an $i$ and $q_i$ be the probability that the second die gives an $i$. Let $p(x)=\sum_{i=0}^5 p_i x^i$ and $q(x)=\sum_{i=0}^5 q_i x^i$.

Let $r(x)=p(x)q(x) = \sum_{i=0}^{10} r_i x^i$. We find that $r_i = \sum_{j+k=i}p_jq_k$. But hey, this is also the probability that the sum of the two dice is $i$. Therefore, $$ r(x)=\frac{1}{11}(1+x+\dots+x^{10}). $$ Now $r(1)=1\neq0$, and for $x\neq1$, $$ r(x)=\frac{(x^{11}-1)}{11(x-1)}, $$ which clearly is nonzero when $x\neq 1$. Therefore $r$ does not have any real zeros.

But because $p$ and $q$ are $5$th degree polynomials, they must have zeros. Therefore, $r(x)=p(x)q(x)$ has a zero. A contradiction.

Answer 10

I like the proof that there are infinitely many Pythagorean triples.

Theorem: There are infinitely many integers $ x, y, z$ such that $$ x^2+y^2=z^2 $$

Proof: $$ (2ab)^2 + ( a^2-b^2)^2= ( a^2+b^2)^2 $$

Answer 11

Given a square consisting of $2n \times 2n$ tiles, it is possible to cover this square with pieces that each cover $2$ adjacent tiles (like domino bricks). Now imagine, you remove two tiles, from two opposite corners of the original square. Prove that is is now no longer possible to cover the remaining area with domino bricks.

Proof:

Imagine that the square is a checkerboard. Each domino brick will cover two tiles of different colors. When you remove tiles from two opposite corners, you will remove two tiles with the same color. Thus, it can no longer be possible to cover the remaining area.

(Well, it may be too "simple." But you did not state that it had to be a university student of mathematics. This one might even work for liberal arts majors...)

Answer 12

One little-known gem at the intersection of geometry and number theory is Aubry's reflective generation of primitive Pythagorean triples, i.e. coprime naturals $\,(x,y,z)\,$with $\,x^2 + y^2 = z^2.\,$ Dividing by $\,z^2$ yields $\,(x/z)^2+(y/z)^2 = 1,\,$ so each triple corresponds to a rational point $(x/z,\,y/z)$ on the unit circle. Aubry showed that we can generate all such triples by a very simple geometrical process. Start with the trivial point $(0,-1)$. Draw a line to the point $\,P = (1,1).\,$ It intersects the circle in the rational point $\,A = (4/5,3/5)\,$ yielding the triple $\,(3,4,5).\,$ Next reflect the point $\,A\,$ into the other quadrants by taking all possible signs of each component, i.e. $\,(\pm4/5,\pm3/5),\,$ yielding the inscribed rectangle below. As before, the line through $\,A_B = (-4/5,-3/5)\,$ and $P$ intersects the circle in $\,B = (12/13, 5/13),\,$ yielding the triple $\,(12,5,13).\,$ Similarly the points $\,A_C,\, A_D\,$ yield the triples $\,(20,21,29)\,$ and $\,(8,15,17),\,$
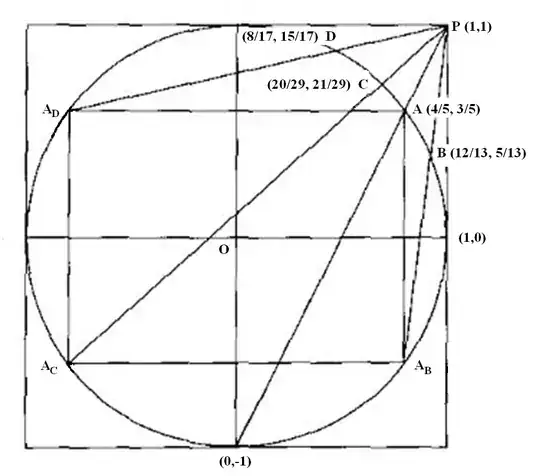
We can iterate this process with the new points $\,B,C,D\,$ doing the same we did for $\,A,\,$ obtaining further triples. Iterating this process generates the primitive triples as a ternary tree

$\qquad\qquad$
Descent in the tree is given by the formula

$$\begin{eqnarray} (x,y,z)\,\mapsto &&(x,y,z)-2(x\!+\!y\!-\!z)\,(1,1,1)\\ = &&(-x-2y+2z,\,-2x-y+2z,\,-2x-2y+3z)\end{eqnarray}$$

e.g. $\ (12,5,13)\mapsto (12,5,13)-8(1,1,1) = (-3,4,5),\ $ yielding $\,(4/5,3/5)\,$ when reflected into the first quadrant.

Ascent in the tree by inverting this map, combined with trivial sign-changing reflections:

$\quad\quad (-3,+4,5) \mapsto (-3,+4,5) - 2 \; (-3+4-5) \; (1,1,1) = ( 5,12,13)$

$\quad\quad (-3,-4,5) \mapsto (-3,-4,5) - 2 \; (-3-4-5) \; (1,1,1) = (21,20,29)$

$\quad\quad (+3,-4,5) \mapsto (+3,-4,5) - 2 \; (+3-4-5) \; (1,1,1) = (15,8,17)$

See my MathOverflow post for further discussion, including generalizations and references.

Answer 13

One cannot cover a disk of diameter 100 with 99 strips of length 100 and width 1.

Proof: project the disk and the strips on a semi-sphere on top of the disk. The projection of each strip would have area at most 1/100th of the area of the semi-sphere.

Answer 14

If you have any set of 51 integers between $1$ and $100$, the set must contain some pair of integers where one number in the pair is a multiple of the other.

Proof: Suppose you have a set of $51$ integers between $1$ and $100$. If an integer is between $1$ and $100$, its largest odd divisor is one of the odd numbers between $1$ and $99$. There are only $50$ odd numbers between $1$ and $99$, so your $51$ integers can’t all have different largest odd divisors — there are only $50$ possibilities. So two of your integers (possibly more) have the same largest odd divisor. Call that odd number $d$. You can factor those two integers into prime factors, and each will factor as (some $2$’s)$\cdot d$. This is because if $d$ is the largest divisor of a number, the rest of its factorization can’t include any more odd numbers. Of your two numbers with largest odd factor $d$, the one with more $2$’s in its factorization is a multiple of the other one. (In fact, the multiple is a power of $2$.)

In general, let $S$ be the set of integers from $1$ up to some even number $2n$. If a subset of $S$ contains more than half the elements in $S$, the set must contain a pair of numbers where one is a multiple of the other. The proof is the same, but it’s easier to follow if you see it for a specific $n$ first.

Answer 15

The proof that an isosceles triangle ABC (with AC and AB having equal length) has equal angles ABC and BCA is quite nice:

Triangles ABC and ACB are (mirrored) congruent (since AB = AC, BC = CB, and CA = BA), so the corresponding angles ABC and (mirrored) ACB are equal.

This congruency argument is nicer than that of cutting the triangle up into two right-angled triangles.

Answer 16

I believe Gauss was tasked with finding the sum of all the integers from $1$ to $100$ in his very early schooling years. He tackled it quicker than his peers or his teacher could, $$\sum_{n=1}^{100}n=1+2+3+4 +\dots+100$$ $$=100+99+98+\dots+1$$ $$\therefore 2 \sum_{n=1}^{100}n=(100+1)+(99+2)+\dots+(1+100)$$ $$=\underbrace{101+101+101+\dots+101}_{100 \space times}$$ $$=101\cdot 100$$ $$\therefore \sum_{n=1}^{100}n=\frac{101\cdot 100}{2}$$ $$=5050.$$ Hence he showed that $$\sum_{k=1}^{n} k=\frac{n(n+1)}{2}.$$

Answer 17

how about deriving Binets formula for Fibonacci numbers based on the characteristic polynomial:

$$ f_n = \frac{\phi^n - \psi^n}{ \sqrt{5}} $$

Answer 18

Parity of sine and cosine functions using Euler's forumla:

$e^{-i\theta} = cos\ (-\theta) + i\ sin\ (-\theta)$

$e^{-i\theta} = \frac 1 {e^{i\theta}} = \frac 1 {cos\ \theta \ + \ i\ sin\ \theta} = \frac {cos\ \theta\ -\ i\ sin\ \theta} {cos^2\ \theta\ +\ sin^2\ \theta} = cos\ \theta\ -\ i\ sin\ \theta$

$cos\ (-\theta) +\ i\ sin\ (-\theta) = cos\ \theta\ +i\ (-sin\ \theta)$

Thus

$cos\ (-\theta) = cos\ \theta$

$sin\ (-\theta) = -\ sin\ \theta$

$\blacksquare$

The proof is actually just the first two lines.

Answer 19

If $H$ is a subgroup of $(\mathbb{R},+)$ and $H\bigcap [-1,1]$ is finite and contains a positive element. Then, $H$ is cyclic.

Answer 20

Euler's solution to the Basel problem using the (unjustified at the time) Weierstrass factorization theorem. Eventually led to reading Hardy's Divergent Series with understanding coming in fits and starts.

Answer 21

Proposition (No universal set): There does not exists a set which contain all the sets (even itself)

Proof: Suppose to the contrary that exists such set exists. Let $X$ be the universal set, then one can construct by the axiom schema of specification the set

$$C=\{A\in X: A \notin A\}$$

of all sets in the universe which did not contain themselves. As $X$ is universal, clearly $C\in X$. But then $C\in C \iff C\notin C$, a contradiction.

Edit: Assuming that one is working in ZF (as almost everywhere :P)

(In particular this proof really impressed me too much the first time and also is very simple)

Answer 22

Fermat's little theorem from noting that modulo a prime p we have for $a\neq 0$:

$$1\times2\times3\times\cdots\times (p-1) = (1\times a)\times(2\times a)\times(3\times a)\times\cdots\times \left((p-1)\times a\right)$$

Answer 23

Most proofs concerning the Cantor Set are simple but amazing.

The total number of intervals in the set is zero.

It is uncountable.

Every number in the set can be represented in ternary using just 0 and 2. No number with a 1 in it (in ternary) appears in the set.

The Cantor set contains as many points as the interval from which it is taken, yet itself contains no interval of nonzero length. The irrational numbers have the same property, but the Cantor set has the additional property of being closed, so it is not even dense in any interval, unlike the irrational numbers which are dense in every interval.

The Menger sponge which is a 3d extension of the Cantor set simultaneously exhibits an infinite surface area and encloses zero volume.

Answer 24

The derivation of first principle of differentiation is so amazing, easy, useful and simply outstanding in all aspects. I put it here:

Suppose we have a quantity $y$ whose value depends upon a single variable $x$, and is expressed by an equation defining $y$ as some specific function of $x$. This is represented as:

$y=f(x)$

This relationship can be visualized by drawing a graph of function $y = f (x)$ regarding $y$ and $x$ as Cartesian coordinates, as shown in Figure(a).

Consider the point $P$ on the curve $y = f (x)$ whose coordinates are $(x, y)$ and another point $Q$ where coordinates are $(x + Δx, y + Δy)$.

The slope of the line joining $P$ and $Q$ is given by:

$tanθ = \frac{Δy}{Δx} = \frac{(y + Δy ) − y}{Δx}$

Suppose now that the point $Q$ moves along the curve towards $P$.

In this process, $Δy$ and $Δx$ decrease and approach zero; though their ratio $\frac{Δy}{Δx}$ will not necessarily vanish.

What happens to the line $PQ$ as $Δy→0$, $Δx→0$? You can see that this line becomes a tangent to the curve at point $P$ as shown in Figure(b). This means that $tan θ$ approaches the slope of the tangent at $P$, denoted by $m$:

$m=lim_{Δx→0} \frac{Δy}{Δx} = lim_{Δx→0} \frac{(y+Δy)-y}{Δx}$

The limit of the ratio $Δy/Δx$ as $Δx$ approaches zero is called the derivative of $y$ with respect to $x$ and is written as $dy/dx$.

It represents the slope of the tangent line to the curve $y=f(x)$ at the point $(x, y)$.

Since $y = f (x)$ and $y + Δy = f (x + Δx)$, we can write the definition of the derivative as:

$\frac{dy}{dx}=\frac{d{f(x)}}{dx} = lim_{x→0} [\frac{f(x+Δx)-f(x)}{Δx}]$,

which is the required formula.

Answer 25

This proof that $n^{1/n} \to 1$ as integral $n \to \infty$:

By Bernoulli's inequality (which is $(1+x)^n \ge 1+nx$), $(1+n^{-1/2})^n \ge 1+n^{1/2} > n^{1/2} $. Raising both sides to the $2/n$ power, $n^{1/n} <(1+n^{-1/2})^2 = 1+2n^{-1/2}+n^{-1} < 1+3n^{-1/2} $.

Answer 26

Can a Chess Knight starting at any corner then move to touch every space on the board exactly once, ending in the opposite corner?

The solution turns out to be childishly simple. Every time the Knight moves (up two, over one), it will hop from a black space to a white space, or vice versa. Assuming the Knight starts on a black corner of the board, it will need to touch 63 other squares, 32 white and 31 black. To touch all of the squares, it would need to end on a white square, but the opposite corner is also black, making it impossible.

Answer 27

The Eigenvalues of a skew-Hermitian matrix are purely imaginary.

The Eigenvalue equation is $A\vec x = \lambda\vec x$, and forming the vector norm gives $$\lambda \|\vec x\| = \lambda\left<\vec x, \vec x\right> = \left<\lambda \vec x,\vec x\right> = \left<A\vec x,\vec x\right> = \left<\vec x, A^{T*}\vec x\right> = \left<\vec x, -A\vec x\right> = -\lambda^* \|\vec x\|$$ and since $\|\vec x\| > 0$, we can divide it from left and right side. The second to last step uses the definition of skew-Hermitian. Using the definition for Hermitian or Unitarian matrices instead yields corresponding statements about the Eigenvalues of those matrices.

Answer 28

I like the proof that not every real number can be written in the form $a e + b \pi$ for some integers $a$ and $b$. I know it's almost trivial in one way; but in another way it is kind of deep.