1

This question is based on the diagram

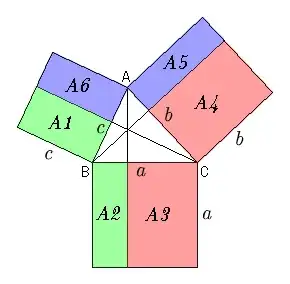
alt text

taken from this link. I don't understand why the areas of A6 and A5 adds up to $2bc\cos(A)$.

Arturo Magidin
  • 398,050
Sara
  • 1,249
  • 1
    http://en.wikipedia.org/wiki/Law_of_cosines#Proofs – Quixotic Nov 17 '10 at 19:16
  • Few days ago I noticed this discussion:http://meta.math.stackexchange.com/questions/132/stop-tagging-things-with-the-tag-proofs – Quixotic Nov 17 '10 at 19:17
  • 2
    Here's my version of that diagram: http://math.stackexchange.com/questions/803/what-is-the-most-elegant-proof-of-the-pythagorean-theorem/1336#1336 – Blue Nov 18 '10 at 02:19

2 Answers2

1

The other side of A6 has length $c \cos A$ and that of A5 length $b \cos A.$

So their total area is $b \times c \cos A + c \times b \cos A = 2bc \cos A.$

Derek Jennings
  • 13,531
1

If you look at A5. It is a rectangle with side $b$ and, say, $x$. Now $\cos A= x/c$, so $x=c\cos A$. Hence the area of A5 is $bx=bc\cos A$.

A similar argument tells you that the area of A6 is $cb\cos A$.

AD - Stop Putin -
  • 10,970