I am trying to get some intuition about the simplest flag manifold $ U(2)/T^2 $ which is apparently given by $ CP^1\cong S^2 $ . I have understood the stereographic projection of $ S^2 $ onto the complex plane. But I don't understand how $ U(2)/T^2 \cong CP^1 $. Can anyone tell me how this projection works?
-
Counter question for calibration: Do you understand the set of complex lines through the origin in $\mathbf{C}^2$, and do you understand the stereographic projection picture in this setting? – Andrew D. Hwang Jul 20 '13 at 00:06
-
1No. I can imagine it has to do with using the usual argument of using unit vectors in $ C^2 $ as rays and each of these rays correspond to a unique point on $ CP^1 $ . How do rigorously write down the transformation. – enigmae Jul 20 '13 at 15:40
1 Answers
Here's a picture:
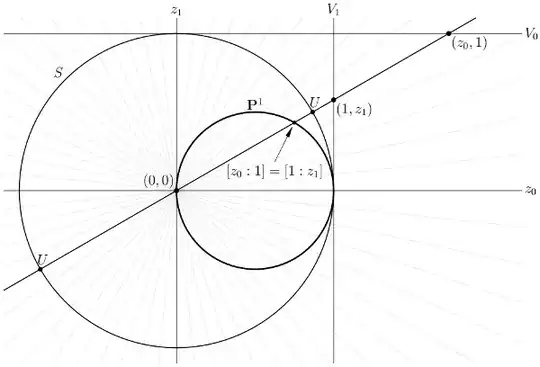
First, view the picture "literally", as $\mathbf{R}^2$ equipped with Cartesian coordinates $(z_0, z_1)$. Every real line through the origin crosses at least one of the lines $V_1 = \{z_0=1\}$ or $V_0 = \{z_1=1\}$. (The $z_0$-axis misses $V_0$, the $z_1$-axis misses $V_1$.) Each "affine coordinate neighborhood" $V_i$ is a "copy" of $\mathbf{R}$, and the respective affine coordinates are related by $z_0z_1 = 1$.
The circle of unit vectors in $\mathbf{R}^2$ is denoted $S$. Each real line through the origin cuts $S$ in a unit $0$-sphere, i.e., in a pair of antipodal points (labeled $U$).
Further, each real line hits the circle labeled $\mathbf{P}^1$ exactly twice: once at the origin, and once at an arbitrary point of the circle. (The $z_1$-axis is tangent to the small circle, i.e., "hits the circle twice at the origin".) Consequently, the real projective line may be viewed as the small circle. Projection away from the origin is stereographic projection from $\mathbf{P}^1$ to the affine coordinate neighborhood $V_1$.
Now view the picture "figuratively", as $\mathbf{C}^2$, and think of complex lines through the origin. The affine coordinate neighborhoods are defined exactly as before. Each is a "copy" of $\mathbf{C}$ in $\mathbf{C}^2$, and except for the axes, every complex line through the origin hits each affine coordinate neighborhood exactly once.
The set $S$ of unit vectors is the $3$-sphere $S^3$, and each complex line through the origin intersects $S$ in a unit circle $U$. (These circles are the "fibres of the Hopf map".)
In this interpretation, $\mathbf{P}^1$ is not sitting in $\mathbf{C}^2$ in a nice way; however, it may still be viewed abstractly as the result of attaching the two complex lines $V_0$ and $V_1$ by identifying $z_1$ and $1/z_0$, so the complex projective line is a real $2$-sphere.
So, finally, the original question boils down to: The group $U(2)$ of unitary $2 \times 2$ matrices acts transitively on the space of complex lines through the origin in $\mathbf{C}^2$, and the stabilizer of a line is isomorphic to a real $2$-torus. (Each coordinate axis is invariant by the diagonal subgroup, for example.)
- 78,195
-
Firstly, I would like to thank you for the time and effort you have taken to answer my question. Secondly, I was wondering why you have considered 2 subspaces $ V_0 , V_1 $. Can we rather just consider one of them and assume that line along $ z_1 $ axis meets $ V_1 $ at infinity($ \pm $)? – enigmae Jul 20 '13 at 23:22
-
You're very welcome. :) The introduction of two lines makes your intuition about infinity precise, by ensuring that every line properly hits one of the coordinate neighborhoods. (If you consider the projective plane, the set of lines through the origin in a three-dimensional space, the need for multiple coordinate systems becomes more apparent; it's potentially tricky to see what happens at infinity otherwise.) – Andrew D. Hwang Jul 21 '13 at 01:19