$\newcommand{\Number}[1]{\mathbf{#1}}\newcommand{\Cpx}{\Number{C}}\newcommand{\Reals}{\Number{R}}\newcommand{\Proj}{\mathbf{P}}\newcommand{\dd}{\partial}$This is not a complete answer, but a collection of hints and geometric insights expanding my comment.
Exercise 2.1 from A Beginner's Guide to Holomorphic Manifolds
Consider the following descriptions of the complex projective line $\Proj^{1}$:
- The unit sphere $\{(u, v, w) \in \Reals^{3} \mid u^{2} + v^{2} + w^{2} = 1\}$, which is identified with the "Riemann sphere" $\Cpx \cup \infty$ by stereographic projection.
- Two copies of the complex line $\Cpx$ suitably glued together. More precisely, let $z^{0}$ and $z^{1}$ be complex coordinates in the two copies of $\Cpx$, and identify $z^{0}$ with $1/z^{1}$. In this picture, the origin in each copy of $\Cpx$ is the point at infinity in the other copy.
- The set of non-zero pairs of complex numbers $(Z^{0}, Z^{1}) \in \Cpx^{2} \setminus (0, 0)$, with the equivalence relation $(Z^{0}, Z^{1}) \sim (W^{0}, W^{1})$ if and only if $Z^{0} W^{1} = Z^{1} W^{0}$, i.e. the points $(Z^{0}, Z^{1})$ and $(W^{0}, W^{1})$ lie on the same complex line through $(0, 0)$. In other words, a point of $\Proj^{1}$ is a line through the origin in $\Cpx^{2}$.
Show that these three descriptions are equivalent by using the identification $z^{0} = Z^0/Z^{1}$. (A sketch of the real points may be helpful.) Describe the space of holomorphic vector fields on $\Proj^{1}$ in terms of each presentation; determine, in particular, which vector fields correspond to rotations of the sphere. Describe the space of holomorphic 1-forms on $\Proj^{1}$ and the space of meromorphic 1-forms dual to holomorphic vector fields.
First, a sketch of the real points, from here:
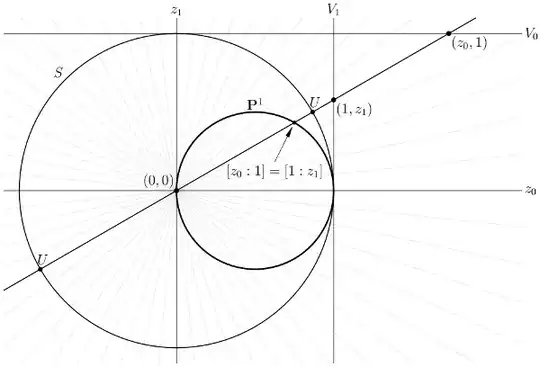
Part 1. Here, stereographic projection means stereographic projection using the north pole and the equatorial plane. There is an omitted pitfall that ought to be mentioned: The other chart is not stereographic projection from the south pole (to/from the equatorial plane), but stereographic projection from the south pole composed with complex conjugation.
This picture was mentioned first because it is geometrically concrete, and seemed likeliest of the three to be familiar to a reader. Further, a reader is likely to have seen Möbius transformations,
$$
T(z) = \frac{az + b}{cz + d},\quad ad - bc \neq 0,
$$
in complex analysis, and may have geometric intuition about visualizing translation, rotation, and dilation of the plane as mappings on the sphere. (On the sphere: translation and dilation. Rotation of the plane about $0$ is rotation of the sphere about the axis through the south and north poles.) See also the award-winning short film Möbius Transformations Revealed by Douglas Arnold and Jonathan Rogness.
Part 2. Let's write $z^{0} = z$ and $z^{1} = w$ for simplicity. The formal point is, the tangent bundle is trivialized in the $z$-plane by the constant vector field $\dd/\dd z$ and in the $w$-plane by $\dd/\dd w$. We want first to see how these are related in the overlap, where $w = 1/z$ and $z = 1/w$. The chain rule says
$$
\frac{\dd}{\dd w} = \frac{\dd z}{\dd w}\, \frac{\dd}{\dd z},
$$
and elementary calculus provides the derivative.
Let $f$ and $g$ denote entire functions. One way to find the space of holomorphic vector fields is to write
$$
f(z)\, \frac{\dd}{\dd z} = g(w)\, \frac{\dd}{\dd w}
$$
in the overlap. Expand each of $f$ and $g$ as power series, then use $w = 1/z$ and $\dd/\dd w = -z^{2}\, \dd/\dd z$ to express the right-hand side as a Laurent series in $z$, multiplied by $\dd/\dd z$. All but three coefficients necessarily vanish, leaving a three-dimensional space of holomorphic vector fields.
Unjustified (but plausible?) claims:
- $\dd/\dd z$ is infinitesimal translation in the $z$-plane. This vector field vanishes at infinity (to order $2$, in fact, either algebraically or from the "dipole" behavior of the flow), in agreement with geometric intuition and the animation linked above.
- The Euler vector field $z\, \dd/\dd z$ is infinitesimal dilation, while $iz\, \dd/\dd z$ is infinitesimal rotation.
- $-z^{2}\, \dd/\dd z = \dd/\dd w$ is infinitesimal translation in the $w$-plane.
A short digresssion about differential forms: Similarly, the cotangent bundle is trivialized in the $z$-plane by the constant one-form $dz$ and in the $w$-plane by $dw$. The chain rule says
$$
dz = \frac{\dd z}{\dd w}\, dw.
$$
The "holomorphic" one-form $dz$ has a pole (of order $2$) at infinity! (Compare the double zero of $\dd/\dd z$ at infinity.)
Small rant I: Partly I dislike the ISO standard $\mathrm{d}z$ (N.B. upright d) because I think it's ugly; partly it involves gratuitous extra typing and invites nitpicky "corrections" to MSE posts. But underneath it all, it's because
To a geometer "$dz$" isn't "a small amount of $z$", it's an associated section of the cotangent bundle. It is one single symbol that happens to be composed of two characters.
Small rant II: Many students successfully learn to manipulate and evaluate line and surface integrals in vector calculus, then hit a wall upon encountering differential forms in a course on manifolds. To the extent this impression is correct, mathematicians have Successfully Buried familiar computational idioms in the languages of vector bundles and local trivializations, sheaves of smooth sections, pullbacks, and naturality of exterior differentiation.
Strictly speaking, if we define a mapping $\phi(z) = 1/z = w$ on the punctured plane, then $\phi^{*}\, dw = -(1/z^{2})\, dz$. But in practice, we write $dw = -dz/z^{2}$. To emphasize:
Computing a pullback means using algebraic substitution and the chain rule to perform change of coordinates on a differential form.
<>
Part 3. Automorphisms of the complex projective line are (or may be identified with) invertible linear transformations on $\Cpx^{2}$, modulo complex non-zero scaling. The qualitative idea is straightforward: Linear automorphisms of $\Cpx^{2}$ preserve complex lines through the origin. Conversely, from complex analysis every holomorphic automorphism of the Riemann sphere is effected by a Möbius transformation
$$
z \mapsto T(z) = \frac{az + b}{cz + d}.
$$
But in our identifications,
$$
z = \left[\begin{array}{@{}c@{}}
z \\
1 \\
\end{array}\right]
= \left[\begin{array}{@{}c@{}}
Z^{0} \\
Z^{1} \\
\end{array}\right] \mapsto
T(z) = \left[\begin{array}{@{}c@{}}
\frac{az + b}{cz + d} \\
1 \\
\end{array}\right]
= \left[\begin{array}{@{}c@{}}
az + b \\
cz + d \\
\end{array}\right]
= \left[\begin{array}{@{}c@{}}
aZ^{0} + bZ^{1} \\
cZ^{0} + dZ^{1} \\
\end{array}\right].
$$
This is (the transformation induced by) a linear automorphism of $\Cpx^{2}$.
