6

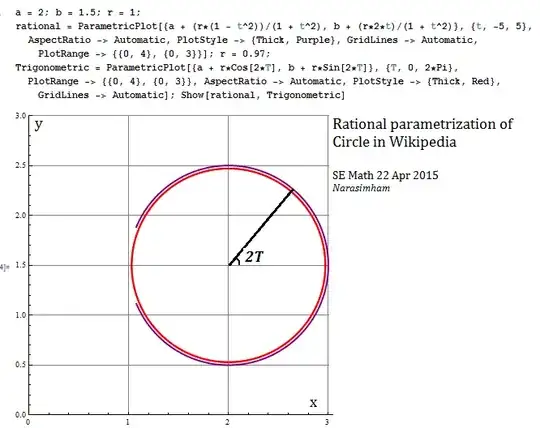
In http://en.wikipedia.org/wiki/Circle but also in the corresponding article in the German Wikipedia I find this formulation ( sorry, I exchange x and y as I am accustomed to it in this way ) :

"An alternative parametrisation of the circle is: $$x=a+r\frac{1-t^2}{1+t^2}$$ and $$y=b+r\frac{2t}{1+t^2}$$ with real-valued parameter $t$."

But if I plot this curve I only get a half-circle with these formulas when $(a,b)\neq(0,0)$ which is obviously not what is searched for and expected.

I recently found without any elementary trigonometry e.g. for the unit circle with $(a,b)=(1,0)$ a closed rational parametrization which plots the "whole" circle perfectly if $\lim_{t\to\infty}$.

Now my 2 questions:

  1. What is your formula for the case of the unit circle with $(a,b)=(1,0)$ and how is your way to derive it ?
  2. Is there a way to calculate a rational parametrization for the unit circle with general $(a,b)$ which allows "whole"-circle plotting ? Maybe $a$ and $b$ must be rational numbers or even integers ?
Michael Hardy
  • 1
Wolfgang Tintemann
  • 755

2 Answers2

9

Write $$ f(t)=\frac{1-t^2}{1+t^2} $$ and $$ g(t)=\frac{2t}{1+t^2} $$ The point should be that $(f(t))^2+(g(t))^2=1$ so that $(f(t),g(t))=(\cos \theta,\sin\theta)$ for some angle $\theta$. It is easy to see that

  1. $f(t)=0\iff t=\pm 1$ and
  2. $f(t)>0\iff |t|<1$ and
  3. $f(t)=1\iff t=0$

It is also easy to see that

  1. $g(t)=0\iff t=0$ together with
  2. $g(t)>0\iff t>0$ and
  3. $|g(t)|=1\iff |t|=1$

But $f(t)=-1$ is never reached. Analyzing $f$ and $g$, we see that $$ t\to-\infty\implies f(t)\to -1, g(t)\to 0_- $$ and $$ t\to+\infty\implies f(t)\to -1, g(t)\to 0_+ $$ so to have a full circle (except for one point at $(-1,0)$) we must have $t\in\mathbb R$.

enter image description here

As you can see, it is like having one period of $\cos\theta$ and $\sin\theta$ reparametrized to $f(t)=\cos(\theta(t))$ and $g(t)=\sin(\theta(t))$ such that $\theta(t)\to-\pi$ for $t\to-\infty$ and $\theta(t)\to\pi$ for $t\to\infty$.

String
  • 18,395
  • I want to mention that I was puzzled because I have the following parametrization of the shifted unit circle with the parameter only running in $[0,\infty)$ $$x(t)=2(\frac{1-t^2}{1+t^2})^2$$ $$y(t)=2\frac{2t(1-t^2)}{(1+t^2)^2}$$ – Wolfgang Tintemann Apr 22 '15 at 17:11
  • 2
    @Wolfgang: The curve $(x, y)$ in your comment traces the small circle here; since$$2\cos\theta = 2f(t) = 2\frac{1 - t^{2}}{1 + t^{2}},$$your curve is $x(t) = 2\cos^{2}\theta$, $y(t) = 2\sin\theta \cos\theta$, which traces the polar graph $r = 2\cos\theta$. As you say, letting $t$ range over $[0, \infty)$ traces the right half of the large circle (stereographic projection from $(0, 1)$), but all of the small circle. This trick works because your circle passes through the origin. – Andrew D. Hwang Apr 22 '15 at 17:41
  • If I understand you the radius of the circle $S$ in your ( for me very surprising ) picture is the $2$ in the case above. So if the small circle is turned by an angle maybe for it might ( sometimes ) also exist rational parametrization formulas ? – Wolfgang Tintemann Apr 22 '15 at 18:09
  • There is a good video explaining the 1 + t^2 rational parameterization here: https://www.youtube.com/watch?v=OqxYLyGLqcs – cessationoftime Aug 10 '23 at 05:14
4

Wiki form is correct. However, along with the so-called "advantage" of rational parametric form comes the limitation of infinite argument requirement to complete a deep circle.

For y to be zero or x to attain its extremum value you expect for single parameter $t$ have a reasonable domain for full circular arc description. But it is not so.. as one root of $t$ is at $t=0$ and another one at $ t= \infty$.

A trigonometric expression remedies the situation fully by expressing coordinates in terms of double angle $ 2 T$ ( double of half angle in Weierstrass form ) given in Wiki.( Actually I recommend its deletion or insertion of trig form as Wiki is a central reference).

$$ x = a + r \cos (2 T) ;\; y = b + r \sin (2 T) ; $$

TrigCircle

The Mathematica code is given in the image.I have slightly reduced rational circle radius to show full circle by trigonometrical parametrization by contrast.

As an aside the particular trig representation of Circle has significance in Mechanics of Structures. When y_offset = 0, it is the Mohr Circle, first used by famous German civil engineer Otto Mohr who defined static determinacy and constructed very useful diagrams of stress and strain. The angle $T$ represents angle between reference direction of stress and principal stress.

Standard form with half angle in trigonometric $$x = h + r \sin \theta ; \; y = k + r \sin \theta $$ serves the same purpose, it is simpler.

Narasimham
  • 40,495