2

I am going through Nakahara's "Geometry, topology and physics" by myself and I got stuck on a calculation.

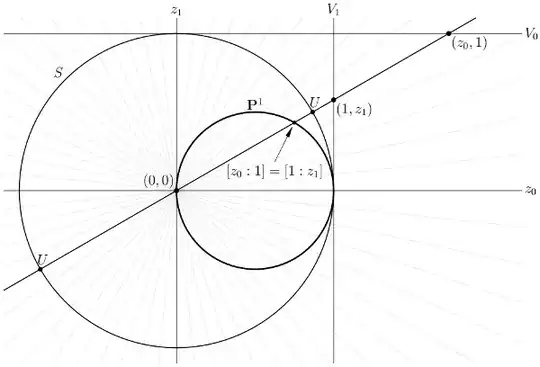
I have the total space $$L=\{(p,v)\in\mathbb{C}P^n\times\mathbb{C}^{n+1}|v=ap,a\in\mathbb{C} \} $$ and the projection map $\pi:L\rightarrow\mathbb{C}P^n$ as $\pi(p,v)=p.$

So far I have that the fibre is then $\mathbb{C}^{n+1}$ over $\mathbb{C}P^n$ and that the trivialization is the map $\phi_i^{-1}:\pi(p,v)\rightarrow U_k\times\mathbb{C}^{n+1}$ where $\{U_k\}$ is a n open cover of $\mathbb{C}P^n\simeq\mathbb{C}$ with coordinates $(z_0/z_1,z_1/z_2\dots z_n/z_0)$.

So I thought that the trivialization is then $\phi_i(v)=(p,\frac{z_k}{|z_{k+1}|})$ and the transition function is $t_{ij}=\frac{z_k|z_{j+1}|}{|z_{k+1}|z_j} $.

the group structure is $G\supset \{t_{kj}\}$.

I am a bit out of my depth here so any help is greatly appreciated.

Jean Marie
  • 81,803
Fredovich
  • 63

1 Answers1

2

$\newcommand{\Cpx}{\mathbf{C}}\newcommand{\Proj}{\mathbf{P}}$First, a small note on terminology: Nowadays it's common to call the line bundle $L$ the tautological bundle. The term "canonical" bundle almost universally connotes the top exterior power of the cotangent bundle.

The standard trivialization of the tautological line bundle over $U_{k}$ is given by the (non-vanishing local holomorphic) section $$ \sigma_{k}[z_{0} : \dots : z_{n}] = \bigl(\underbrace{[z_{0} : \dots : z_{n}]}_{\in \Cpx\Proj^{n}}, \underbrace{z_{0}/z_{k}, \dots, z_{n}/z_{k}}_{\in \Cpx^{n+1}}\bigr). $$ The $\Cpx^{n+1}$ components are ratios of homogeneous coordinates, and therefore well-defined local functions; together they span the line represented by $[z_{0} : \dots : z_{n}]$. The transition function is $t_{ij} = z_{i}/z_{j}$.

The diagram below (taken from Flag manifold to Complex Projective line) shows the two local sections for the projective line.

Lines through the origin in the plane

Community
  • 1
Andrew D. Hwang
  • 78,195
  • So the inverse of trivialization is then $\phi^{-1}([z_0:\dots:z_n],z_0/z_k,\dots z_n/z_k)=[z_0:dots :z_n$? Is the structure group then $U(n)$? – Fredovich Jan 08 '17 at 15:56
  • Almost: The map you give is the bundle projection, which sends the fibre of $L$ at a point $[p]$ to $[p]$. By "trivialization given by a section" I meant: If $w_{1}$, ..., $w_{n}$, $t$ are complex numbers, then$$\phi_{k}(w, t) = \bigl([w_{1}: \dots: w_{k-1}: 1: w_{k}: \dots: w_{n}], tw_{1}, \dots, tw_{k-1}, t, tw_{k}, \dots, tw_{n}\bigr).$$The structure group of the tautological line bundle is $U(1)$ (assuming the bundle is equipped with an Hermitian structure). – Andrew D. Hwang Jan 08 '17 at 16:42
  • Okej, thanks. The complex part makes me really uncertain and I don't know why. – Fredovich Jan 08 '17 at 16:55
  • I know it's super late, but I am struggling to understand the tautological line bundle. Like it is a line bundle, so isn't the fiber everywhere $\cong\mathbb C$? I couldn't see that from the action of $\sigma_k$ here as the result $\in\mathbb{CP}^n\times\mathbb C^{n+1}$. @AndrewD.Hwang – N00BMaster Mar 22 '24 at 13:53
  • @N00BMaster Yes, the fibers of the tautological bundle are complex lines. Specifically, the tautological fiber over a point of projective space is the complex line in affine space represented by that point. Take care to distinguish the codomain $\mathbf{CP}^{n}\times\mathbf{C}^{n+1}$ of the section $\sigma_{k}$ and its image, compare my previous comment to OP. – Andrew D. Hwang Mar 22 '24 at 20:40