5

I am solving some exercises in a book I'm reading and so far all the exercises contained some insight. But then I got to the following exercise:

Let $z,a\in \mathbb C$. Show that

$$ (1-|z|^2)(1-|a|^2) =|1-z\overline{a}|^2 - |z-a|^2$$

Then deduce from this that if $|a|<1$ then

$$ |z|<1 \iff \left| {z-a \over \overline{a}z -1} \right|<1$$

and

$$ |z|=1 \iff \left| {z-a \over \overline{a}z -1} \right|=1$$

What is the insight to be had from this exercise?

All the other exercises were insightful but this one here seems to be just computational.

Note that this is part b) of the exercise. Part a) was:

Let $\mathbb H := \{z \in \mathbb C \mid \operatorname{Im}{z}>0 \}$. Show that $z \in \mathbb H$ if and only if $-{1\over z}\in \mathbb H$.

I solved part a) and I feel that it should be somehow related to part b) but I don't know how.

Anna
  • 1,757

1 Answers1

5

$\newcommand{\Cpx}{\mathbf{C}}$You're secretly describing certain automorphisms (holomorphic bijections with holomorphic inverse) of the open unit disk.

The open unit disk plays a starring role in complex analysis: It turns out that every connected, simply-connected, proper open subset of the complex plane is "biholomorphic" to the open disk (the so-called Riemann mapping theorem).

Edit: There was a mistake in my original answer, in that part (b) doesn't describe all automorphisms of the disk, but only a certain family of involutions (automorphisms that are their own inverse).

To fill in some of the background, here's a brief sketch of the Riemann sphere as the complex projective line, Möbius transformations as $2 \times 2$ complex matrices, and a more detailed interpretation of part (b).

The complex projective line is the set of (complex) lines through the origin in $\Cpx^{2}$. Algebraically, consider ordered pairs $(z_{0}, z_{1})$ of complex numbers (not both zero) modulo the equivalence relation $$ (z_{0}, z_{1}) \sim (\lambda z_{0}, \lambda z_{1})\quad\text{for all $\lambda \neq 0$.} $$ Associating $z$ in $\Cpx$ with the line through $(z, 1)$ (labeled $V_{0}$ in the figure below), we represent every line except the line through $(1, 0)$; since $(z, 1) \sim (1, \frac{1}{z})$ for $z \neq 0$, it's reasonable to view $(1, 0)$ as "$\infty$"; doing this identifies the complex projective line with the Riemann sphere. (There's a bit more detail in another post, from which the following figure is recycled.)

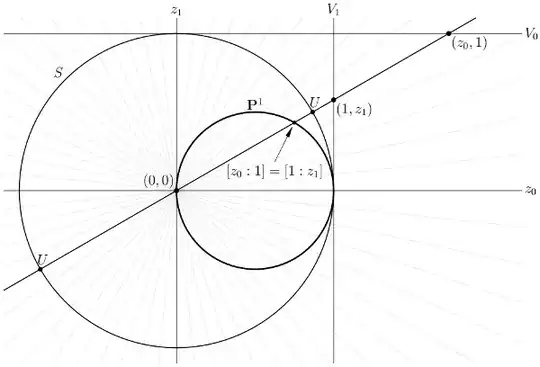
The complex projective line

An "automorphism" of the projective line/Riemann sphere is a bijection that is meromorphic in the local coordinate $z$. To make a moderately lengthy story short, every automorphism of the projective line turns out to be induced by a linear automorphism of $\Cpx^{2}$, via the correspondence $$ \left[\begin{array}{@{}rr@{}} a & b \\ c & d \\ \end{array}\right] \left[\begin{array}{@{}c@{}}z \\ 1\end{array}\right] = \left[\begin{array}{@{}c@{}} az + b \\ cz + d\end{array}\right] \sim \left[\begin{array}{@{}c@{}}\dfrac{az + b}{cz + d} \\ 1\end{array}\right],\quad ad - bc \neq 0. $$ (This is the origin of the term "fractional linear" transformation.) In particular, composition of Möbius transformations corresponds to matrix multiplication.

The coefficient matrix can be multiplied by a non-zero constant without changing the associated Möbius transformation, and it's customary to normalize by taking $ad - bc = 1$, i.e., to identify projective automorphisms with $SL(2, \Cpx)/{\pm}$.

As to part (b) of your question: The Möbius transformation $f(z) = \dfrac{z - a}{\overline{a}z - 1}$ corresponds to the matrix $$ A = \left[\begin{array}{@{}rr@{}} 1 & -a \\ \overline{a} & -1 \end{array}\right]. $$ Part (b) asserts that if $|a| < 1$, then $|z| < 1$ if and only if $|f(z)| < 1$, and $|z| = 1$ if and only if $|f(z)| = 1$. In other words, $f$ maps the open unit disk to itself, and maps the unit circle to the unit circle. Moreover, $A^{2} = (1 - |a|^{2}) I \sim I$, so $f$ is an involution of the disk.

Incidentally, the mapping $g(z) = -1/z$ in part (a) is an involution of the upper half plane. It's not difficult to show that the Möbius transformations $$ \phi(z) = \frac{z - i}{z + i} \leftrightarrow \left[\begin{array}{@{}rr@{}} 1 & -i \\ 1 & i \\ \end{array}\right],\quad \phi^{-1}(z) = i\frac{1 + z}{1 - z} \leftrightarrow \left[\begin{array}{@{}rr@{}} i & i \\ -1 & 1 \\ \end{array}\right] $$ map the open upper half plane to the open disk (and vice versa), and it's an easy exercise to check that $(\phi \circ g \circ \phi^{-1})(z) = -z$, the "$a = 0$" mapping in part (b).

Community
  • 1
Andrew D. Hwang
  • 78,195
  • 1
    Thank you for your answer, it is exactly what I was hoping for. But is there any way you could elaborate on how this exercise will describe all automorphisms of the open unit disk? (and is part a) relevant at all?) – Anna Mar 07 '15 at 00:30
  • 1
    @Anna: The extent to which this exercise describes all automorphisms of the disk depends on how much you know at this stage about Moebius (fractional linear) transformations. :) But at any rate (b) shows that a particular Moebius transformation is a disk automorphism. (Part (a) is not needed for (b), but does show that $z \mapsto -1/z$ is a involution of the upper half-plane.) – Andrew D. Hwang Mar 07 '15 at 00:54
  • 1
    Just to let you know: I am still working on this question. Your comment helped me. But I know nothing about Moebius transforms at this point and in response to your answer I am now trying to read up on Moebius transforms. – Anna Mar 09 '15 at 09:42
  • On Wikipedia it says that ''The Möbius transformations are exactly the bijective conformal maps from the Riemann sphere to itself, i.e., the automorphisms of the Riemann sphere as a complex manifold; '' But in the exercise only $a$ is variable, $b,c$ and $d$ are given. How do I see that by fixing these the automorphism of a sphere becomes that of a disk? – Anna Mar 09 '15 at 10:02
  • @Anna: I've added some background material on Moebius transformations and corrected a factual error in my original answer; part (b) doesn't describe all disk automorphisms. – Andrew D. Hwang Mar 09 '15 at 14:58
  • 1
    Thank you, your edit helped me. – Anna Mar 15 '15 at 01:46
  • I realised there is still something I don't understand: These Moebius transforms map the unit disk to the unit disk. But what is the unit disk in the Riemann sphere? Is it the set $S$ in your picture? Wouldn't that mean that the metric on the Riemann sphere and $\mathbb R^2$ are the same? – Anna Mar 18 '15 at 01:17
  • The other thing I am not clear about is the link between part a) and part b): what is the significance of the map $\phi \circ g \circ \phi^{-1}$? – Anna Mar 18 '15 at 02:00
  • @Anna: Viewing the Riemann sphere as the unit sphere in $\mathbf{R}^{3}$, identified with \mathbf{C}$ by stereographic projection from the "north pole", then the unit disk is the "southern hemisphere". (In the diagram, this is the left semi-circle on $\mathbf{P}^{1}$, corresponding to the set of $(z_{0}, 1)$ with $|z_{0}| < 1$. The set $S$ is the unit $3$-sphere in $\mathbf{C}^{2}$; "dimensional lying" is unavoidable since we can't draw $\mathbf{C}^{2}$ accurately.) The composition $\phi \circ g \circ \phi^{-1}$ is the disk automorphism corresponding to $a = 0$, namely, $z \mapsto -z$. :) – Andrew D. Hwang Mar 18 '15 at 13:25