I need help in the following question. I'm not sure how to even begin to answer this. What is a possible proof for the following question?
If $A$ is an $m \times n$ matrix and $b$ is an $m$-vector, prove that the solution $x$ of minimum Euclidean norm to the least-squares problem $A\cong B$ is given by $$x=\sum_{\sigma_i \neq 0} \frac{u_i^Tb}{\sigma_i}v_i$$ where the $\sigma_i$, $u_i$, and $v_i$ are the singular values and corresponding singular vectors of A.
Preliminaries
Start with a tighter specification on the target matrix: $$ \mathbf{A} \in \mathbb{C}^{m\times n}_{\rho} $$ where the rank $\rho < \min (m,n)$. The matrix is rank defective and both null spaces are nontrivial.
We are given the data vector $b\notin\color{red}{\mathcal{N}\left( \mathbf{A}^{*} \right)}$ to insure a least squares solution exists. Defining the vector of residual errors $$ r(x) = \mathbf{A} x - b, $$ the desire is to find the solution vector $x$ which minimizes the total error $r^{2}$. The solution set is given by the minimizers $$ x_{LS} = \left\{ x\in\mathbb{C}^{n} \colon \lVert \mathbf{A} x - b \rVert_{2}^{2} \text{ is minimized} \right\} $$ For each element in this set, $r^{2}\left(x_{LS}\right)$ achieves minimum value. We are searching for the element in this set which has minimum length.
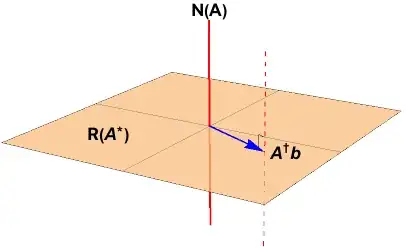
In Laub's book (p. 66), he shows the solution is in general an affine space:
represented as the dashed red line in the figure below.
The singular value decomposition is $$ \begin{align} \mathbf{A} &= \mathbf{U} \, \Sigma \, \mathbf{V}^{*} \\ % &= % U \left[ \begin{array}{cc} \color{blue}{\mathbf{U}_{\mathcal{R}}} & \color{red}{\mathbf{U}_{\mathcal{N}}} \end{array} \right] % Sigma \left[ \begin{array}{cc} \mathbf{S}_{\rho\times \rho} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} \end{array} \right] % V \left[ \begin{array}{c} \color{blue}{\mathbf{V}_{\mathcal{R}}}^{*} \\ \color{red}{\mathbf{V}_{\mathcal{N}}}^{*} \end{array} \right] \\ % \end{align} $$ The Moore-Penrose pseudoinverse is constructed from the SVD: $$ \begin{align} \mathbf{A}^{\dagger} &= \mathbf{V} \, \Sigma^{\dagger} \, \mathbf{U}^{*} \\ % &= % U \left[ \begin{array}{cc} \color{blue}{\mathbf{V}_{\mathcal{R}}} & \color{red} {\mathbf{V}_{\mathcal{N}}} \end{array} \right] % Sigma \left[ \begin{array}{cc} \mathbf{S}^{-1} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} \end{array} \right] % V \left[ \begin{array}{c} \color{blue}{\mathbf{U}_{\mathcal{R}}}^{*} \\ \color{red} {\mathbf{U}_{\mathcal{N}}}^{*} \end{array} \right] \\ % \end{align} $$ The object of the proof is to show that the pseudoinverse solution has minimum length.
Trick
Cast the total error in terms of the SVD and perform a unitary transformation $$ r^{2}(x) = \lVert \mathbf{A} x - b\rVert_{2}^{2} = \lVert \mathbf{U} \, \Sigma \, \mathbf{V}^{*} x - b \rVert_{2}^{2} = \lVert \Sigma \, \mathbf{V}^{*} x - \mathbf{U}^{*} b \rVert_{2}^{2} $$ to separate the $\color{blue}{range}$ and $\color{red}{null}$ spaces. $$ \begin{align} r^{2}(x) = \lVert \Sigma \, \mathbf{V}^{*} x - \mathbf{U}^{*} b \rVert_{2}^{2} &= \Bigg\lVert \left[ \begin{array}{cc} \mathbf{S} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} \\ \end{array} \right] \left[ \begin{array}{c} \color{blue}{\mathbf{V}_{\mathcal{R}}}^{*} \\ \color{red} {\mathbf{V}_{\mathcal{N}}}^{*} \end{array} \right] x - \left[ \begin{array}{c} \color{blue}{\mathbf{U}_{\mathcal{R}}}^{*} \\ \color{red} {\mathbf{U}_{\mathcal{N}}}^{*} \end{array} \right] b \Bigg\rVert_{2}^{2} \\ % &= \big\lVert \mathbf{S} \color{blue}{\mathbf{V}_{\mathcal{R}}}^{*} x - \color{blue}{\mathbf{U}_{\mathcal{R}}}^{*} b - \color{red} {\mathbf{U}_{\mathcal{N}}}^{*} b \big\rVert_{2}^{2} \\ % &= \big\lVert \mathbf{S} \color{blue}{\mathbf{V}_{\mathcal{R}}}^{*} x - \color{blue}{\mathbf{U}_{\mathcal{R}}}^{*} b \big\rVert_{2}^{2} + \big\lVert \color{red} {\mathbf{U}_{\mathcal{N}}}^{*} b \big\rVert_{2}^{2} \\ % \end{align} $$ How to minimize the total error now? We control the range space component, and we force that contribution to $0$: $$ r^{2}(x) = \underbrace{\big\lVert \mathbf{S} \color{blue}{\mathbf{V}_{\mathcal{R}}}^{*} x - \color{blue}{\mathbf{U}_{\mathcal{R}}}^{*} b \big\rVert_{2}^{2}}_{\text{controlled}} + \underbrace{\big\lVert \color{red} {\mathbf{U}_{\mathcal{N}}}^{*} b \big\rVert_{2}^{2}}_{\text{uncontrolled}} \\ $$ That is, force $$ \mathbf{S} \color{blue}{\mathbf{V}_{\mathcal{R}}}^{*} x - \color{blue}{\mathbf{U}_{\mathcal{R}}}^{*} b = 0 $$ by setting $$ \color{blue}{x_{LS}} = \color{blue}{\mathbf{V}_{\mathcal{R}}}\mathbf{S}^{-1}\color{blue}{\mathbf{U}_{\mathcal{R}}}^{*} b = \color{blue}{\mathbf{A}^{\dagger} b}. $$ The least value for the sums of the squares of residuals is $$ r^{2}\left( x_{LS} \right) = \big\lVert \color{red} {\mathbf{U}_{\mathcal{N}}}^{*} b \big\rVert_{2}^{2} $$ The derivation deliberately avoided the requirement that $\mathbf{A}$ be of full column rank. When the null space $\color{red}{\mathcal{N}\left( \mathbf{A}^{*} \right)}$ is nontrivial, the least squares solution includes a projection onto that null space. The least squares solution set is $$ x_{LS} = \color{blue}{\mathbf{A}^{\dagger}b} + \color{red} {\left( \mathbf{I}_{n} - \mathbf{A}^{\dagger} \mathbf{A} \right)y}, \quad y\in\mathbb{C}^{n} $$ Refer back to the blue vector and red dashed line in the previous figure.
What are the lengths of the least squares solution vectors?
$$ \lVert x_{LS} \rVert_{2}^{2} = \lVert \color{blue}{\mathbf{A}^{\dagger}b} \rVert_{2}^{2} + \lVert \color{red} {\left( \mathbf{I}_{n} - \mathbf{A}^{\dagger} \mathbf{A} \right)y}\rVert_{2}^{2} $$
What the least squares solution of minimum length?
It is the vector which is entirely in $\color{blue}{\mathcal{N}\left( \mathbf{A}^{*} \right)}$. It is the pseudoinverse solution.
$$ \lVert \color{blue}{x_{LS}} \rVert_{2}^{2} = \lVert \color{blue}{\mathbf{A}^{\dagger}b} \rVert_{2}^{2} $$
