I've read somewhere that:
$x=A^+b+(I-A^+A)Z$ is a solution for $Ax=b$ ,when is doesn't have a particular solution.
where $A^+$ indicates the pseudo-inverse and $Z$ is an arbitrary vector!!!
I know The first term represents the least square solution but the second term is said to be can used for optimizing secondary criteria and is called the "homogeneous solution". What is homogeneous solution? Where does it come from?
Linear system
Given the matrix $\mathbf{A}\in\mathbb{C}^{m\times n}_{\rho}$, and data vector $b\in\mathbb{C}^{m}$, the linear system $$ \mathbf{A} x = b $$ will have a least squares solution provide that $b\notin\color{red}{\mathcal{N}\left(\mathbf{A}^{*}\right)}$.
Least squares solution The least squares solution is defined as $$ x_{LS} = \left\{ x \in \mathbb{C}^{n} \colon \lVert \mathbf{A} x - b \rVert_{2}^{2} \text{ is minimized} \right\} \tag{1} $$
As you noted, the least squares solution can be written as $$ x_{LS} = \color{blue}{\mathbf{A}^{+} b} + \color{red}{\left( \mathbf{I}_{n} - \mathbf{A}^{+} \mathbf{A} \right) y}, \quad y\in\mathbb{C}^{n} \tag{2} $$
Fundamental projector
The right hand component is the fundamental projector onto the $\color{red}{null}$ space $\color{red}{\mathcal{N}\left(\mathbf{A}\right)}$ $$ \mathbf{P}_{\color{red}{\mathcal{N}\left(\mathbf{A}\right)}} = \color{red}{\left( \mathbf{I}_{n} - \mathbf{A}^{+} \mathbf{A} \right)} $$ The least squares solution is the affine space represented by the $\color{red}{red}$, dashed lined. The projector projects vectors onto this $\color{red}{null}$ space. (Note the solution of minimum norm is $\color{blue}{x_{+}} = \color{blue}{\mathbf{A}^{+}b}$.)
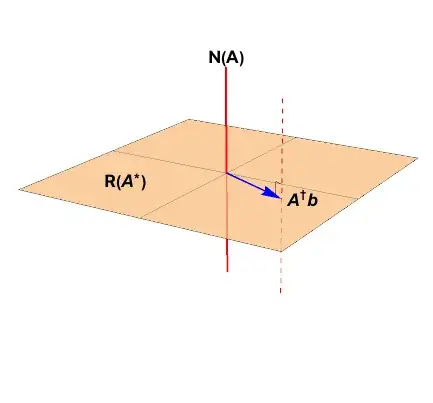
Full column rank
When the matrix $\mathbb{A}$ has full column rank, $\rho = n$,
the null space $\color{red}{\mathcal{N}\left( \mathbf{A} \right)} = \mathbf{0}$
$\mathbf{P}_{\color{red}{\mathcal{N}\left(\mathbf{A}\right)}} \color{red}{\left( \mathbf{I}_{n} - \mathbf{A}^{+} \mathbf{A} \right)} = \left( \mathbf{I}_{n} - \mathbf{I}_{n} \right) = \mathbf{0}$
least squares solution is the point $ \color{blue}{x_{+}} = \color{blue}{\mathbf{A}^{+}b}, $
This is the point in the range space $\color{blue}{\mathcal{R}\left(\mathbf{A}^{*}\right)}$
Read more
A bit more background is in Singular value decomposition proof.
$$ \begin{align} % \mathbf{A} x &= b \\ % \left[ \begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array} \right] % \left[ \begin{array}{c} x_{1} \\ x_{2} \end{array} \right] % &= \left[ \begin{array}{c} b_{1} \\ b_{2} \end{array} \right] \end{align} $$ If $b_{1}\ne0$, the least squares solution exists. Another way to state this condition is $$ b\notin\color{red}{\mathcal{N}\left( \mathbf{A}^{*}\right)} $$
For $b_{2}\ne0$, the general least squares solution can be written as $$ x_{LS} = \color{blue}{\left[ \begin{array}{c} b_{1} \\ 0 \end{array} \right]} + \alpha \color{red}{\left[ \begin{array}{c} 0 \\ 1 \end{array} \right]}, \quad \alpha \in \mathbb{C} $$ The fundamental projector onto the null space $\color{red}{\mathcal{N}\left(\mathbf{A}\right)}$ is $$ \mathbf{P}_{\color{red}{\mathcal{N}\left(\mathbf{A}\right)}} = \color{red}{\left[ \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array} \right]} $$ When $b_{2}=0$, the data vector $b$ is in the $\color{blue}{range}$ space $\color{blue}{\mathcal{R}\left(\mathbf{A}\right)}$, and there is a direct solution $$ x = \color{blue}{x_{LS}} = \color{blue}{\left[ \begin{array}{c} b_{1} \\ 0 \end{array} \right]} $$ The direct solution is the least squares solution which is a point in the range space.
The general solution to the homogeneous system of linear equations $Ax=0$ is given by $(I-A^+A)Z$. Hence the name.
