The most comprehensive answer to your question may be here: Singular value decomposition proof. Laub's theorem presents a shortcut to the answer.
Preliminaries
Adapt the notation common to the cross-linked posts. Given a matrix $\mathbf{A}\in\mathbb{C}^{m\times n}_{\rho}$, a data vector $b\in\mathbb{C}^{m}$ which is not in the null space $\color{red}{\mathcal{N}\left(\mathbf{A}^{*} \right)}$ find the least squares solutions defined as
$$
x_{LS} = \left\{
x\in\mathbb{C}^{n} \colon \lVert
\mathbf{A} x - b
\rVert_{2}^{2}
\text{ is minimized}
\right\}
$$
As seen in Laub's book (see first crosslink), the general least squares solution is the affine set
$$
x_{LS} = \color{blue}{\mathbf{A}^{+}b} +
\color{red}{\left( \mathbf{I} - \mathbf{A}^{+} \mathbf{A} \right) y}, \quad y\in\mathbb{C}^{n}
$$
The point solution is in the range space $\color{blue}{\mathcal{R}\left(\mathbf{A}\right)}$, the hyperplane is the projection onto the null space $\color{red}{\mathcal{N}\left(\mathbf{A} \right)}$.
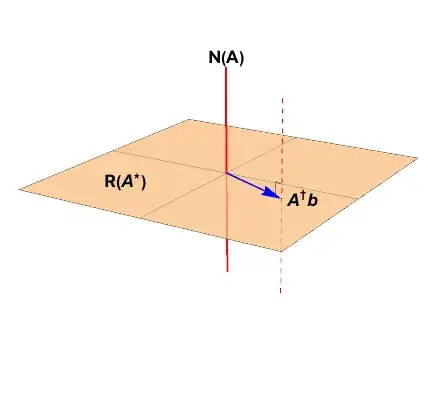
First question
There are derivations in the following posts which may help. Let's take another perspective.
The resort to least squares in an admission that the data vector $b$ has a null space component
$$
b = {\color{blue}{b_\mathcal{R}}} + {\color{red}{b_\mathcal{N}}}
$$
And there is no solution such that $\mathbf{A}x = b$; there is no combination of columns of $\mathbf{A}$ which produces $b$. The least squares solution finds the projection of the data vector onto the range space $\color{blue}{\mathcal{R}{\left(\mathbf{A}\right)}}$.
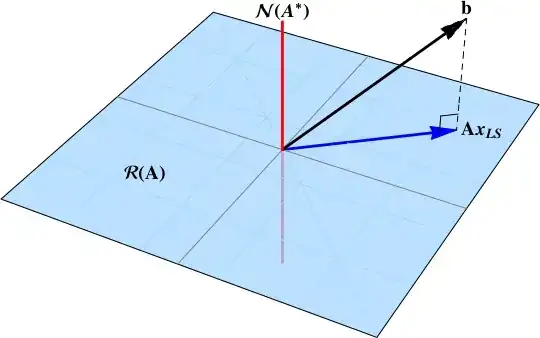
The solution is
$$
\mathbf{A} x = \color{blue}{b_{\mathcal{R}}} +
\color{red}{\left(\mathbb{I}_{n} - \mathbf{A}^{*}\mathbf{A} \right) y}=
\color{blue}{\mathbf{A}^{+} b} +
\color{red}{\left(\mathbb{I}_{n} - \mathbf{A}^{*}\mathbf{A} \right) y}, \quad y\in\mathbb{C}^{n}
$$
The general rank deficient matrix and least squares:
How does the SVD solve the least squares problem?
The general least squares solution: Why does SVD provide the least squares solution to $Ax=b$?
Second question
Why is the least squares solution a point instead of an affine space when the matrix has full column rank? Or, why is the least squares solution unique when the target matrix has full column rank?
The null space $\color{red}{\mathcal{N}\left( \mathbf{A} \right)}$ is trivial. The solution space is entirely in $\color{blue}{\mathcal{R}\left(\mathbf{A} \right)}$
Equivalence of the normal equations solution and the pseudoinverse:
How to find the singular value decomposition of $A^{T}A$ & $(A{^T}A)^{-1}$
The full column rank least squares solution: Solution to least squares problem using Singular Value decomposition

