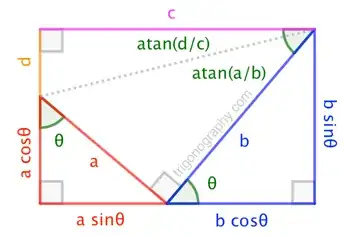
Suppose that there is a trigonometric equation of the form $a\sin x + b\cos x = c$, where $a,b,c$ are real and $0 < x < 2\pi$. An example equation would go the following: $\sqrt{3}\sin x + \cos x = 2$ where $0<x<2\pi$.
How do you solve this equation without using the method that moves $b\cos x$ to the right side and squaring left and right sides of the equation?
And how does solving $\sqrt{3}\sin x + \cos x = 2$ equal to solving $\sin (x+ \frac{\pi}{6}) = 1$
The idea is to use the identity $\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$. You have $a\sin x+b\cos x$, so you’d like to find an angle $\beta$ such that $\cos\beta=a$ and $\sin\beta=b$, for then you could write
$$a\sin x+b\cos x=\cos\beta\sin x+\sin\beta\cos x=\sin(x+\beta)\;.$$
The problem is that $\sin\beta$ and $\cos\beta$ must be between $-1$ and $1$, and $a$ and $b$ may not be in that range. Moreover, we know that $\sin^2\beta+\cos^2\beta$ must equal $1$, and there’s certainly no guarantee that $a^2+b^2=1$.
The trick is to scale everything by $\sqrt{a^2+b^2}$. Let $A=\dfrac{a}{\sqrt{a^2+b^2}}$ and $B=\dfrac{b}{\sqrt{a^2+b^2}}$; clearly $A^2+B^2=1$, so there is a unique angle $\beta$ such that $\cos\beta=A$, $\sin\beta=B$, and $0\le\beta<2\pi$. Then
$$\begin{align*} a\sin x+b\cos x&=\sqrt{a^2+b^2}(A\sin x+B\cos x)\\ &=\sqrt{a^2+b^2}(\cos\beta\sin x+\sin\beta\cos x)\\ &=\sqrt{a^2+b^2}\sin(x+\beta)\;. \end{align*}$$
If you originally wanted to solve the equation $a\sin x+b\cos x=c$, you can now reduce it to $$\sqrt{a^2+b^2}\sin(x+\beta)=c\;,$$ or $$\sin(x+\beta)=\frac{c}{\sqrt{a^2+b^2}}\;,$$ where the new constants $\sqrt{a^2+b^2}$ and $\beta$ can be computed from the given constants $a$ and $b$.
Riffing on @Yves' "little known" solutions ...
The above trigonograph shows a scenario with $a^2 + b^2 = c^2 + d^2$, for $d \geq 0$, and we see that $$\theta = \operatorname{atan}\frac{a}{b} + \operatorname{atan}\frac{d}{c} \tag{1}$$ (If the "$a$" triangle were taller than the "$b$" triangle, the "$+$" would become "$-$". Effectively, we can take $d$ to be negative to get the "other" solution.) Observe that both $c$ and $d$ are expressible in terms of $a$, $b$, $\theta$: $$\begin{align} a \sin\theta + b \cos\theta &= c \\ b \sin\theta - a\cos\theta &= d \quad\text{(could be negative)} \end{align}$$ Solving that system for $\sin\theta$ and $\cos\theta$ gives $$\left.\begin{align} \sin\theta &= \frac{ac+bd}{a^2+b^2} \\[6pt] \cos\theta &= \frac{bc-ad}{a^2+b^2} \end{align}\quad\right\rbrace\quad\to\quad \tan\theta = \frac{ac+bd}{bc-ad} \tag{2}$$ We can arrive at $(2)$ in a slightly-more-geometric manner by noting $$c d = (a\sin\theta + b \cos\theta)d = c( b\sin\theta - a \cos\theta ) \;\to\; ( b c - a d)\sin\theta = \left( a c + b d \right)\cos\theta \;\to\; (2) $$ where each term in the expanded form of the first equation can be viewed as the area of a rectangular region in the trigonograph. (For instance, $b c \sin\theta$ is the area of the entire figure.)
Using complex numbers, and setting $z=e^{i\theta}$,
$$a\frac{z-z^{-1}}{2i}+b\frac{z+z^{-1}}2=c,$$ or
$$(b-ia)z^2-2cz+(b+ia)=0.$$
The discriminant is $c^2-b^2-a^2:=-d^2$, assumed negative, then the solution
$$z=\frac{c\pm id}{b-ia}.$$
Taking the logarithm, the real part $$\ln\left(\dfrac{\sqrt{c^2+d^2}}{\sqrt{a^2+b^2}}\right)=\ln\left(\dfrac{\sqrt{c^2+a^2+b^2-c^2}}{\sqrt{a^2+b^2}}\right)=\ln(1)$$ vanishes as expected, and the argument is
$$\theta=\pm\arctan\left(\frac dc\right)+\arctan\left(\frac ab\right).$$
The latter formula can be rewritten with a single $\arctan$, using
$$\theta=\arctan\left(\tan(\theta)\right)=\arctan\left(\frac{\pm\dfrac dc+\dfrac ab}{1\mp\dfrac dc\dfrac ab}\right)=\arctan\left(\frac{\pm bd+ac}{bc\mp ad}\right).$$
This is little known, but you can solve the equation without much trigonometry.
WLOG, we can assume that $a^2+b^2=1$ (the coefficients can be normalized). Write
$$a\,S+b\,C=c,\\b\,C=c-aS,\\b^2(1-S^2)=(c-a\,S)^2,\\S^2-2ac\,S+c^2-b^2=0.$$
The solution of the quadratic equation is $$S=ac\pm bd$$ where $d=\sqrt{1-c^2}$. By symmetry,
$$C=bc\mp ad.$$
If you have enough with the values of the sine and the cosine, you can stop here. Otherwise
$$\theta=\arctan\frac SC.$$
For unnormalized $a,b$, the solution is
$$S=\frac{ac\pm bd}{a^2+b^2},\\ C=\frac{bc\mp ad}{a^2+b^2}$$ and $$\color{green}{\theta=\arctan\frac{ac\pm bd}{bc\mp ad}}$$
where $d=\sqrt{a^2+b^2-c^2}$. It does not exist when $a^2+b^2<c^2$.
From the above, one can observe that the solution is also given by
$$\theta=\arctan\frac ab\pm\arctan\frac dc$$ but this takes two (costly) arc tangents instead of one.
I'm assuming $ab\neq 0$, since otherwise trivial. $a\sin x+b\cos x-c=0$
$$\iff a\left(2\sin\frac{x}{2}\cos\frac{x}{2}\right)+b\left(\cos^2\frac{x}{2}-\sin^2\frac{x}{2}\right)-c\left(\sin^2\frac{x}{2} +\cos^2\frac{x}{2}\right)=0$$
$$\stackrel{:\cos^2 \frac{x}{2}\neq 0}\iff (b+c)\tan^2\frac{x}{2}-2a\tan\frac{x}{2}+(c-b)=0$$
If $b+c\neq 0$, then
$$\iff \tan\frac{x}{2}=\frac{a\pm\sqrt{a^2+b^2-c^2}}{b+c}$$
$$\iff x=2\left(\arctan\left(\frac{a\pm\sqrt{a^2+b^2-c^2}}{b+c}\right)+n\pi\right),\, n\in\Bbb Z$$
Real solutions exist iff $a^2+b^2\ge c^2$.
If $b+c=0$, then
$$\iff \tan\frac{x}{2}=\frac{c-b}{2a}\iff x=2\left(\arctan\frac{c-b}{2a}+n\pi\right),\, n\in\Bbb Z$$
https://en.wikibooks.org/wiki/Trigonometry/Simplifying_a_sin(x)_%2B_b_cos(x)
While the above answers perfectly answer your question, you might benefit from taking a look at the above link. It particularly is relevant for the second part of the question and explains how to simplify $f(x) =a\sin(x) + b\cos(x)$ to a single sine function, approaching it both geometrically and algebraically.
Older textbooks often suggested solving such equations via the tan half-angle identities to make an algebraic equation in $t = \tan (x/2)$. For a derivation see https://en.wikipedia.org/wiki/Tangent_half-angle_formula or this math SE question.
In particular,
$$\sin x = \frac{2t}{1+t^2} \\ \cos x = \frac{1-t^2}{1+t^2} \\ \tan x = \frac{2t}{1-t^2} $$
So if $a \sin x + b \cos x = c$ we have $2at + b(1-t^2) = c(1+t^2)$. This is a quadratic in $t$, which we can easily solve, and once we know $t = \tan (x/2)$ we can find $x$. For an example of this method, see this math SE answer.
