Hi all, I am interested to find elementary proof of tangent half angle formula.
My solutions are the following:
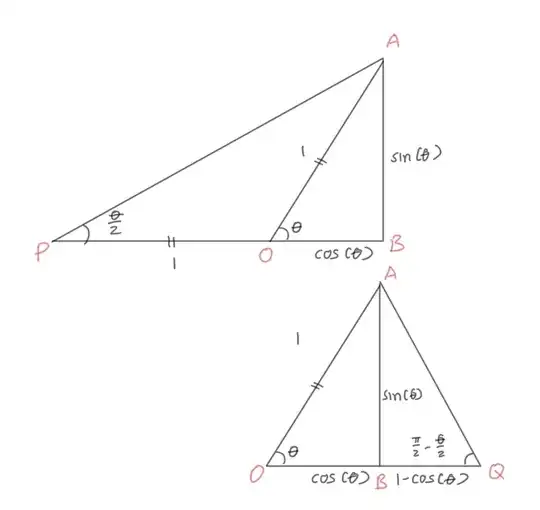
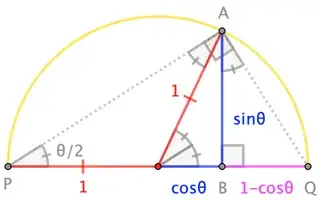
Triangle $AOB$ is such that $|AB|=1$ and $\angle AOB=\theta$. We then extend $OB$ to $P$ and $Q$ such that $|OP|=|OQ|=1$. Thus we will have two isosceles triangles: $AOP$ and $AOQ$.
From the picture, $\tan{\left(\frac{\theta}{2}\right)}=\frac{AB}{BP}=\frac{\sin{\left(\theta\right)}}{1+\cos{\left(\theta\right)}}\ \ \ =\frac{BQ}{AB}=\frac{1-\cos{\left(\theta\right)}}{\sin{\left(\theta\right)}}$
Could You guys please check my solution. I am also wondering if there are other elementary solutions, please share, thanks!