7

I thought this one up, but I am not sure how to solve it. Here is my attempt: $$\sin x-\sqrt{3}\ \cos x=1$$ $$(\sin x-\sqrt{3}\ \cos x)^2=1$$ $$\sin^2x-2\sqrt{3}\sin x\cos x\ +3\cos^2x=1$$ $$1-2\sqrt{3}\sin x\cos x\ +2\cos^2x=1$$ $$2\cos^2x-2\sqrt{3}\sin x\cos x=0$$ $$2\cos x(\cos x-\sqrt{3}\sin x)=0$$ $2\cos x=0\Rightarrow x\in \{\frac{\pi }2(2n-1):n\in\Bbb Z\}$

But how do I solve $$\cos x-\sqrt{3}\sin x=0$$

Martin Sleziak
  • 53,687
clathratus
  • 17,161
  • Observe that the partial "solutions" you got towards the end are false: if for example we take $;n=2;$ , we get $;\frac\pi2\cdot3=\frac{3\pi}2;$ , and at this point sine equals $;-1;$ ...this is due to the fact that when you squared you erased the difference between positive and negative numbers! It is easy to fix this but you must do it. – DonAntonio Nov 10 '18 at 01:27
  • @DonAntonio What do you mean? $(a-b)^2=a^2-2ab+b^2$. Plug in $a=\sin x$, $b=3^{1/2}\cos x$. – clathratus Nov 10 '18 at 01:30
  • When you square an equation you delete any difference between positive and negative solutions: everything becomes positive ! Thus, at the end, it may be you added stuff that doesn't actually solve the equation...just as in your case! Just read and understand my comment above. – DonAntonio Nov 10 '18 at 01:32
  • 2
    Check out R-formula of trigonometry, the answer becomes very clear once you use it – Prashin Jeevaganth Nov 10 '18 at 01:44

6 Answers6

7

Hint: at the very beginning divide both sides by $2$ and use the formula for the sin of difference of 2 arguments

Makina
  • 1,454
  • @clathratus This answer gives the best complete method to solve your original equation. What you did at the end of your question already carries problems because of your squaring. Read comments. +1 – DonAntonio Nov 10 '18 at 01:29
4

Hint :

$$\cos x - \sqrt{3}\sin x = 0 \Leftrightarrow \frac{\sin x}{\cos x} = \frac{\sqrt{3}}{3} \Leftrightarrow \tan x = \frac{\sqrt{3}}{3}$$

Note : You can divide by $\cos x$, since if the case was $\cos x =0$, it would be $\sin x = \pm 1$ and thus the equation would yield $\pm \sqrt{3} \neq 0$, thus no problems in the final solution, as the $\cos$ zeros are no part of it.

Rebellos
  • 21,324
  • But don't we lose zeros when we divide by $\cos x$? – clathratus Nov 10 '18 at 01:19
  • @clathratus No, the exact same $x$ is yielded, because if $\cos x =0$ then the equation isn't equal to $0$, thus it does not hold. – Rebellos Nov 10 '18 at 01:22
  • If $\cos x = 0$ then $\sin x = \pm 1$ and $\cos x - \sqrt 3\sin x = \pm \sqrt 3 \ne 0$. That is not the case. But yes, worrying about losing zeros is important. But if you are afraid of losing zeros.... just do a separate case for them. – fleablood Nov 10 '18 at 01:22
  • @DonAntonio No, the final part of his question is asking this exact equation. – Rebellos Nov 10 '18 at 01:22
  • @Rebellos You're right...yet the OP didn't take into account that when we square probels can pop up. – DonAntonio Nov 10 '18 at 01:24
  • @clathratus One last time: this solves correctly the last equation in your equation... but it doesn't solve the original question. Again, squaring equations many times (like here!) adds trash that must be clead up. – DonAntonio Nov 10 '18 at 01:37
  • @DonAntonio I was confused on what you were trying to say before because you worded it in a confusing way – clathratus Nov 10 '18 at 01:40
  • @clathratus Maybe, but you must check always the "solutions" you get to an equation, any equation, after you squared it. Do this here...! – DonAntonio Nov 10 '18 at 01:41
3

Multiply by the conjugate: $(\cos(x) - \sqrt{3} \sin(x))(\cos(x) + \sqrt{3} \sin(x)) = 0$. Then we have $\cos^2(x)-3\sin^2(x)=0$. This is the same thing as $1-4\sin^2(x)=0$ or $\sin(x)=\pm \frac{1}{2}$.

  • NOTE OF CAUTION: This gives you the answers to both the question and its conjugate. You'd have to plug in and check which ones are the answers you're looking for.
JKreft
  • 232
1

Avoid squaring whenever possible as it immediately introduces extraneous root(s).

$$\sin x-\sqrt3\cos x=1$$

Method$\#1:$

Use Prosthaphaeresis Formulas

Method$\#2:$

Use Solving trigonometric equations of the form $a\sin x + b\cos x = c$

Method$\#3:$

Use Double Angle formula,

$\cos x=\cos^2\dfrac x2-\sin^2\dfrac x2$

and $1-\sin x=\left(\cos\dfrac x2-\sin\dfrac x2\right)^2$

We immediately have $\cos\dfrac x2-\sin\dfrac x2$ as common factor

lab bhattacharjee
  • 274,582
1

You can turn the equation to a polynomial one,

$$s-\sqrt3 c=1$$ is rewritten

$$s^2=1-c^2=(1+\sqrt3c)^2,$$

which yields

$$c=0\text{ or }c=-\frac{\sqrt3}2.$$

Plugging in the initial equation,

$$c=0,s=1\text{ or }c=-\frac{\sqrt3}2,s=-\frac12.$$

Retrieving the angles is easy.

1

It's intersting, I believe, to consider also this other method for solving any linear equation in sine and cosine (provided that the argument is the same for both functions). Recall that cosine and sine are abscissa and ordinate of points on the circumference of radius $1$ and center in the origin of the axes.

Solving your first equation, therefore, is equivalent to finding the interection points between straight line $$r: Y-\sqrt 3 X = 1 $$ and the circumference $$\gamma: X^2+Y^2 = 1.$$ 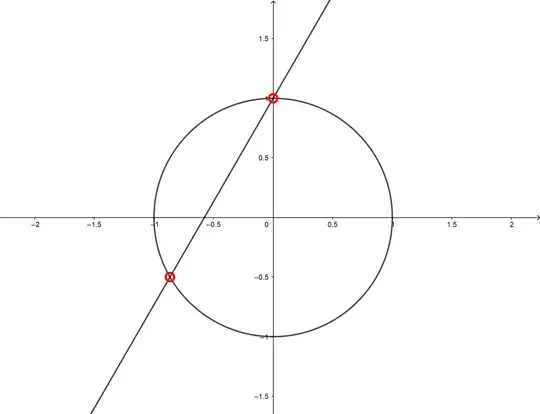enter image description here This brings you the system $$ \begin{cases} Y-\sqrt 3 X = 1\\ X^2+Y^2 = 1. \end{cases} $$ Replacing $Y = \sqrt 3 X + 1$ in the second equation gives you the quadratic equation $$2X^2 +\sqrt 3 X =0,$$ and, from here, to the solutions $$(X_1 = 0, Y_1 = 1)$$ and $$\left(X_2 = -\frac{\sqrt 3}{2}, Y_2 = -\frac{1}{2}\right),$$ with a straightforward trigonometric interpretation.

I leave you as an exercise to apply the same approach to the equation you propose $$\cos x -\sqrt 3 \sin x = 0.$$

Community
  • 1
dfnu
  • 7,528
  • Thank you for the hard work you put into this detailed and interesting answer (+1). I will look over it again when I have time. – clathratus Feb 24 '19 at 05:30