Solution of tanx = x?

Question

How do I find the solutions of tanx = x upto any number of decimals?

(Of course, there is the graphical method but it just helps in finding the approximate value...)

Answer 1

Apart from the solution $x=0$ there are for each $n>0$ two solutions $\pm x_n$ with $x_n={(2n-1)\pi\over2}-\tau_n$ where $\tau_n>0$ is $O({1\over n})$. It is easy to see that $\tau_n$ satisfies the equation $$\tau=\arctan{1\over (2n-1)\pi/2 - \tau}=:f(\tau).$$ As $|f'(\tau)|\ll1$ in the neighbourhood of $\tau=0$ we can obtain $\tau_n$ numerically by iterating $f$ starting at $\tau=0$.

Answer 2

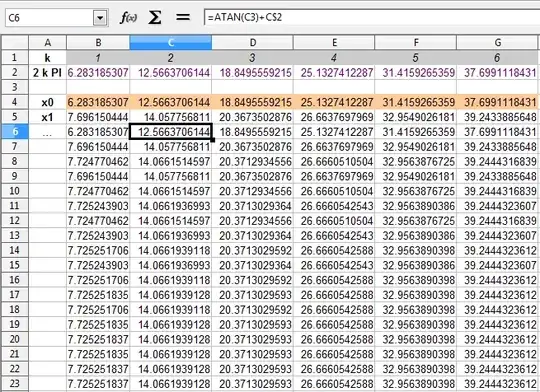
You know that there is a solution $x_k$ in a neighbourhood of $2 \pi k$, for each integer $k$.

And the equation can be also written as

$x_k = \arctan(x_k) + 2 k \pi$

where the arc tangent returns the principal value.

Then you can iterate:

$x_k[0] = 2 k \pi$

$x_k[n] = \arctan(x_k[n-1]) + 2 k \pi$

It converges very quickly - empirically - proof is left as an exercise :)

If you have an starting approximate value, you pick your $k$ by rounding $x_0/(2 \pi)$

Answer 3

Newton-Raphson solving for zeros of $f(x) = tan x - x$

Answer 4

Today, there was a question about the roots of $tan(x)=2x$

I cannot find it. May be this question was delated ?

Nevertheless, I found this question related to $tan(x)=x$ . So, my answer will be to both.

Of course, the roots are transcendantal numbers, which cannot be expressed in terms of a finite number of elementary functions. But they can be expressed on the forme of series :

Answer 5

(This should be a comment to leonbloy's answer)

The proper expression for the fixed-point iteration for the $n$th nonzero solution of $x=\tan\;x$ is $x_{k+1}=\arctan(x_k)+n\pi$. In fact, for the more general transcendental equation $\tan\;x=\lambda x$, the fixed-point iteration $x_{k+1}=\arctan(\lambda x_k)+n\pi$ works nicely; one can use the fixed point starting with $x_0=n\pi$ for the first few iterations and then switch to Newton-Raphson as soon as the fixed-point iteration has started converging. A similar fixed-point method works for the related transcendental equation $\cot\;x=\mu x$.

If one needs to compute large roots, it might be more profitable to construct asymptotic approximations to the roots; details are given in chapter 7 of the book Numerical Methods for Special Functions by Gil, Segura, and Temme.