4

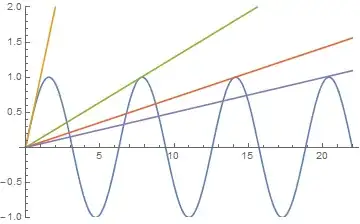
I would like to know if there any analytical methods that can be used to solve this equation. So far, I've made the following observations:

  1. We have to only check for solutions within the domain $-1/m\leq x\leq1/m.$
  2. More than one solution is possible when $0\leq |m|<1.$

I am also guessing that if the slope $0<m\leq \frac{2}{(4n+1)\pi}$ where $n$ is whole number, then the number of solutions $x>0$ will be $2n.$

Student
  • 9,196
  • 8
  • 35
  • 81
  • The equation cannot be solved exactly. You need numerical methods (unless $m=0$ or $m=1$ or perhaps some other cases). – Peter Oct 17 '16 at 09:15
  • Since $0$ is always a solution and $-x$ is a solution whenever $x$ is a solution, we can assume $x>0$. If we have $n$ positive solutions, the number of real solutions is $2n+1$. – Peter Oct 17 '16 at 09:24

2 Answers2

9

I will consider only the case $0<m<1$ and positive solutions. Look at the following picture: enter image description here

There is a sequence $1=m_1>m_2>m_3>\dots$ such that the line $y=m_kx$ is tangent to the graph of $\sin x$ at a point $x_k\in(2\,k\,\pi,2\,k\,\pi+1)$. The equation $\sin x=m\,x$ has

  • $2\,k-1$ solutions if $m=m_k$
  • $2\,k$ solutions if $m_k<m<m_{k+1}$

The values of $x_k$, $m_k$ are the solutions obf the system $$ \sin x=m\,x,\quad\cos x=m. $$ The first values of $m_k$ are $m_1=1$, $m_2=0.128375$, $m_3=0.0709135$, $m_4=0.0490296$.

Julián Aguirre
  • 76,354
  • ... in particular the $x_k$ are solutions of the equation $\tan(x)=x$ (http://math.stackexchange.com/q/18718) – Jean Marie Oct 17 '16 at 10:19
1

You can rewrite as $$\dfrac{\sin x}x=m,$$ and the critical values of $m$ are the extrema of the cardinal sine function.

See https://en.wikipedia.org/wiki/Sinc_function#Properties

They are approximately given by

$$x_n\approx\left(n+\frac12\right)\pi-\frac1{\left(n+\dfrac12\right)\pi}$$

and

$$m_n=\frac{\sin x_n}{x_n}\approx\frac{(-1)^n}{x_n}.$$