Numerical solution to x = tan (x)

Question

I needed to find, using the bisection method, the first positive value that satisfy $x = \tan(x)$. So I went to Scilab, I wrote the bisection method and I got $1.5707903$. But after some reasoning I came to the conclusion that this value is wrong:

$\tan(1.5707903) \approx 1.6x10^5$. Not even close to $1.5707903$.
Forget for a moment the above. $x = \tan(x)$ is actually to find fixed points of $f(x) = \tan(x)$; $(x, f(x))$ must be in the line $y = x$. Here is the plot:

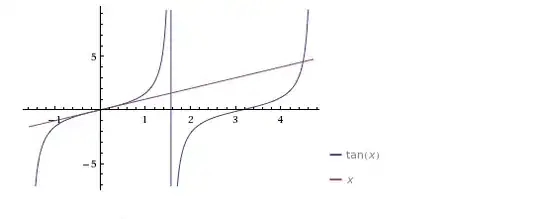
In $(0, \frac{3}{2}\pi)$ I can only see a fixed point to the right of $x = 4$, therefore $1.5707903$ is wrong.

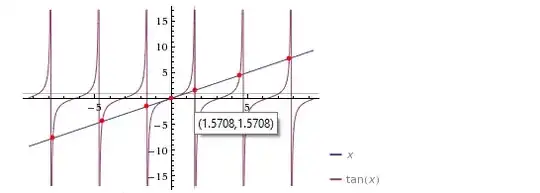
Here comes the interesting part. If you go to Wolfram Alpha and type $x = \tan(x)$, you will see $1.5708$ in the Plot section: x = tan(x)

However there is no $1.5708$ in the Numerical solutions section. Wolfram Alpha found $0, \pm 4.49340945790906, \ldots$.

But if you type $\tan(x) = x$, you will not see $1.5708$ in the Plot section!:

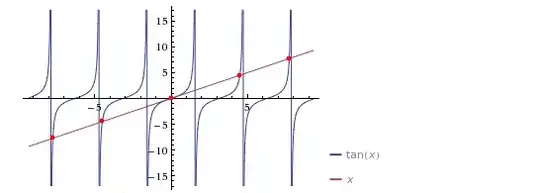
To summarize:

Is $4.49340945790906$ the first positive value that satisfy $x = \tan(x)$?
Do you know why Wolfram Alpha is showing $1.5708$ as a solution when you type $x = \tan(x)$ but not when you type $\tan(x) = x$?

Thanks.

(1) $\tan x$ maps $(-\pi/2,\pi/2)$ bijectively onto $\mathbb{R}$. (2) Moreover, $\tan$ is periodic with period $\pi$. From (1) and (2) it follows that the $x$ we are looking for is in $(\pi/2,3\pi/2)$. — AD - Stop Putin -, Feb 16 '13 at 14:36
BTW bisection is not very fast at all, I would suggest you tried with Newton-Raphson with a starting point like $\pi$. — AD - Stop Putin -, Feb 16 '13 at 14:37
@AD.: I'm interested in your reasoning but I'm not able to follow it. Could you please explain how from (1) and (2) you concluded that the $x$ we are looking for is in $(\pi/2,3\pi/2)$? — David Robert Jones, Feb 16 '13 at 15:08
Bisection would definitively work depending on the choose of starting points they need both to belong in $I_n = (-\pi/2,\pi/2)+\pi\cdot n$ and surround the fixed point. — AD - Stop Putin -, Feb 16 '13 at 15:23
@DavidRobertJones Sorry, I am just about baking cookies with my kid :) — AD - Stop Putin -, Feb 16 '13 at 15:24
@AD.: I'm having a hard time figuring out your reasoning (I think is not quite right). Would you please explain your reasoning? (from (1) and (2) you concluded is in $(\pi/2,3\pi/2)$)? — David Robert Jones, Feb 18 '13 at 15:38
@AD.: For example: $\tan(x)/2$ maps $(−\pi/2,\pi/2)$ bijectively onto $\mathbb{R}$ and is periodic with period $\pi $. But the first positive value that satisfy $x = \tan(x)/2$ is in $(0, \pi/2)$. In this case from (1) and (2) you cannot conclude anything. — David Robert Jones, Feb 18 '13 at 16:07

score 5 · Answer 1 · answered Feb 16 '13 at 15:02

5

As you see from the plot of $\tan x$, you're intercepting the asymptote, which is not really the desired behavior. Bisection is not the best method to use.

However, if you're required to use bisection, then instead note that $\tan x = \frac{\sin x}{\cos x}$, so, for relevant values of $x$,

$$x = \tan x \implies x\cos x - \sin x = 0$$

The latter function is continuous, and you should get the desired solution of $x \approx 4.49$.

answered Feb 16 '13 at 15:02

Emily

35,688
6
93
141

I like your idea. Now I'm wondering: What function would you use as $g(x)$ if you're required to use fixed-point iteration method? – David Robert Jones Feb 16 '13 at 22:28
@DavidRobertJones Offhand, I suspect $\sin^{-1}(x\cos x) = x$ should work, as long you start the iteration in $(0,2\pi)$. – Emily Feb 16 '13 at 23:38
I'm not sure since $\sin^{-1}(x\cos x)$ has no fixed points in the interval. Also don't forget the conditions for convergence. – David Robert Jones Feb 17 '13 at 21:15
@DavidRobertJones It should. I'm not sure if it meets the convergence criteria, but the fixed point should be in $(0,2\pi)$, if the solution is in the interval. – Emily Feb 18 '13 at 03:34
Ah, I know what's wrong... I'm failing to consider the domain of arcsin properly. Maybe substitution exploiting the periodicity of cos will work... I don't know :) – Emily Feb 18 '13 at 03:46

score 4 · Accepted Answer · answered Feb 16 '13 at 14:45

4

The reason you are getting this "solution" is because the bisection method assumes the function is continuous in the range, which it's not. Since the function at both sides of $x=\pi/2$ is $\pm \infty$, the bisection method will always converge to this "solution".

answered Feb 16 '13 at 14:45

Nathaniel Bubis

33,018

Nor is continuous at $[\pi/2,3\pi/2]$ however the solution is there. – David Robert Jones Feb 16 '13 at 15:29
@DavidRobertJones - it's continuous on the open interval. – Nathaniel Bubis Feb 16 '13 at 15:33

score -1 · Answer 3 · answered Jan 23 '18 at 05:58

I have a MathLab code, which is based on bisection method; Here it is:

clc clear % zeros of equation x = tan(x); % The roots of equation x=tanx by means of bisection method % z represents the root % epsilon is error % NR is the number of roots that you want; number of roots = 2*NR+1 % Max is the number of bisections

epsilon = 0.0001; NR = 2; Max = 100;

g=@(x) x-tan(x);

for k = -NR:NR a = (2*k-1)*pi/2 + epsilon; b = (2*k+1)*pi/2 - epsilon; if feval(g,a)*feval(g,b) < 0 for j=1:Max z = (a+b)/2; if (feval(g,a)*feval(g,z) < 0) b=z; elseif (feval(g,a)*feval(g,z) > 0) a=z; end end
if feval(g,z) < epsilon %error
z end end end

% outputs for NR=2 are : -7.7253 , -4.4934 , 0 , 4.4934 , 7.7253

score -1 · Answer 4 · answered Jul 30 '18 at 15:27

-1

1.57 is wrong cause tan π/2 is not defined 3.14/2 is 1.57 hence not defined and can't be termed as the least positive value of tan X = x..hence the lowest positive value is 4.49 for tanx = x

answered Jul 30 '18 at 15:27

Darsh

1

Numerical solution to x = tan (x)

4 Answers4

Linked