1

As part of an engineering problem, I've been trying for a generic solution for $(a\cdot x+b)\cdot \sin(x)+c\cdot \cos(x)=0$

Here's something I tried:

$(a⋅x+b)⋅\tan(x)+c=0$, when $\cos(x)\neq 0$ $$\tan(x)=\frac{-c}{a⋅x+b}$$ It sort of looking like this, when, say, $a=2, b=3, c=5$: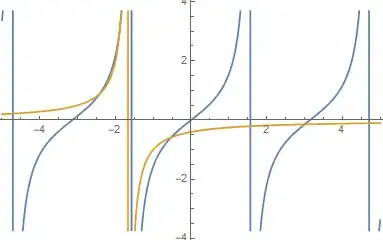a=2, b=3, c=5

Any chance that can be solved without using numerical methods?

EDIT: I was looking for solutions in the form of $x \approx f(a,b,c) $, preferably finding solution in any range, because $a$, $b$, and $c$ can take wierd values. It's used for a program where it will not be trivial to solve problem procedurally.

Community
  • 1
zyc
  • 211

2 Answers2

1

There's no closed form solution for that equation, so numerical methods are required.

That said, you can come up with estimates for the solutions towards $\pm \infty$. For instance, as $n\rightarrow +\infty$, if you write the solutions as $x_n=n\pi + u_n$, with $u_n\in (-\frac \pi 2, \frac \pi 2)$, then $$\tan x_n = \tan u_n = \frac {-c}{ax_n+b}\tag{1}=-\frac c {an\pi + a u_n + b}$$ Because the right-hand side of that equation is equivalent to $-\frac c {a\pi n}$, we must have that $\tan u_n\rightarrow 0$, which means that $u_n\rightarrow 0$. Plugging that information back into (1) yields $$u_n=-\frac c {a\pi n} + v_n$$ where $v_n = o(\frac 1 n)$. And you can now plug this back, again, into (1), and find an estimate for $v_n$. And you keep doing that ad lib to find higher order estimates in the solution $$x_n = n\pi -\frac c {a\pi n} + ....$$

Stefan Lafon
  • 12,256
  • 11
  • 29
  • I'll try that to see if I can rewrite it as $x_n = f(a,b,c)$. I'm not a mathematician, so I'm not really sure. – zyc Dec 13 '18 at 16:22
1

Besides numerical solutions for particular parameter values, you could try series solutions. Thus when $c$ is small compared to $a$ and $b$, the solution near $x=0$ is

$$ -\frac{b}{a} + \cot\left(\frac{b}{a}\right) \frac{c}{a} + \cot\left(\frac{b}{a}\right) \csc^2 \left(\frac{b}{a}\right) \frac{c^2}{a^2} + \left(\cot^3\left(\frac{b}{a}\right) + \cot\left(\frac{b}{a}\right) \sec^4 \left(\frac{b}{a}\right)\right) \frac{c^3}{a^3} + \ldots $$

Robert Israel
  • 448,999
  • $$\left ( \sum_{i=1}^{\infty }\left ( cot^{i}\frac{b}{a}+cot\frac{b}{a}\cdot sec^{2\left ( i-1 \right )}\frac{b}{a} \right )\cdot \frac{c^{i-1}}{a^{i-1}}\mid i\mod 2=1\right )+\left ( \sum_{i=1}^{\infty }\left ( cot^{i}\frac{b}{a}+cot\frac{b}{a}\cdot csc^{2\left ( i-1 \right )}\frac{b}{a} \right )\cdot \frac{c^{i-1}}{a^{i-1}}\mid i\mod 2=0\right )$$ – zyc Dec 13 '18 at 16:03
  • Exactly what I need! Is there a tutorial on how to derive that? – zyc Dec 13 '18 at 16:04