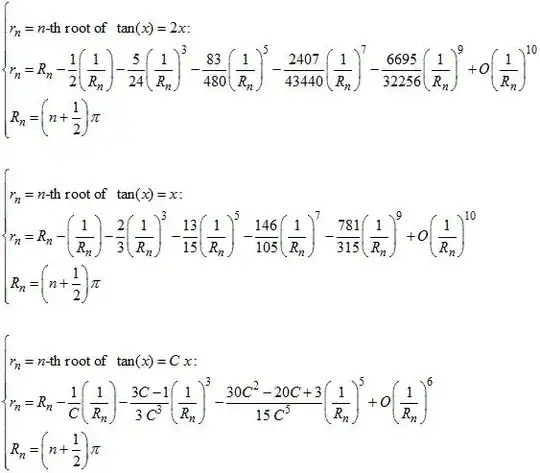Solve $x = \frac{1}{2}\tan(x)$

Question

I did this using trial and error, but I was just wandering if there is an algebraic way of solving this?

I thought about double angle formula but that doesn't work properly does it?

I then tried writing it in the form $x \cdot 2 \cot(x) = 1$ but even then, I can't solve it properly by re-writing $\cot(x)$ because of the $x$ outside the brackets.

Anybody know how I would do this algebraically?

To begin with, a plot will show you that there is exactly one solution in each of the intervals $(-\pi/2 +k\pi,\pi/2+k\pi$. — Julien, Feb 13 '13 at 18:47
I've seen such an equation occur in the context of quantum mechanics, where the eigenvalues of some hamiltonian are given by the set of solutions to such an equation. I strongly suspect there is no "nice" way to find these solutions, however, insofar as there is no combination of elementary functions that'll give you the solutions (save $x = 0$). Instead, it's more interesting to develop asymptotics for these solutions. The idea is to approximate $\tan$ by vertical lines at $\frac{\pi}{2} + k \pi$ as $k$ ranges over the integers. — A Blumenthal, Feb 13 '13 at 18:53
I work with such a functions pretty often, so I confirm - there's no "nice" solution for it. They can be found numerically though, and that's what we do. — Kaster, Feb 13 '13 at 18:56
@Kaish: Here is a plot and here are numerical solutions to go along with the other comments. Regards — Amzoti, Feb 13 '13 at 19:01
As GEdgar remarks, this has come up before. See Derivation of asymptotic solution of $\tan (x)=x$ and Solution of $\tan x = x$? and The Remarkable Equation $\tan x = x$ (the last one is for the notes I used in an April 2006 talk I gave on the solutions). — Dave L. Renfro, Feb 13 '13 at 19:19
Explicit series solution for inverse of $\frac{\tan(x)}x$ here. Your equation is $\frac{\tan(x)}x=2$ — Тyma Gaidash, Aug 20 '23 at 12:33

score 1 · Answer 1 · answered Feb 25 '14 at 12:00

1

Of course, the roots are transcendantal numbers, which cannot be expressed in terms of a finite number of elementary functions. But they can be expressed on the forme of series :

enter image description here

answered Feb 25 '14 at 12:00

JJacquelin

66,221
3
37
87

score -3 · Accepted Answer · answered Feb 13 '13 at 19:02

-3

It cannot be solved algebraically as it is a transcendental equation.

answered Feb 13 '13 at 19:02

user62067

104

4

There are trascendental equations that can be solved algebraically. For instance, $\sin x = \cos x$. – vonbrand Feb 14 '13 at 01:38

Solve $x = \frac{1}{2}\tan(x)$

2 Answers2

Linked

Related