How to solve equations containing trigonometric functions and powers

Question

I mean, is there a way to solve analytically something like this:

$$ \tan(x) - x = 0 $$

or like this equation

$$ \tan(x) - x^2 = 0 $$

I know this will produce infinite number of roots but could they be represented by some simple formula?

Answer 1

By looking at the plot of the $\tan$ function, you observe that the straight line $y=x$ tangents it (no pun) at the origin, then crosses the curve near the vertical asymptotes at $x=\pm(k+\frac12)\pi$ for integer $k>0$.

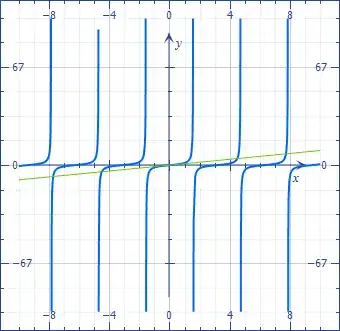
Because of the singularity, these values cannot be taken as starting values for Newton iterations. We can work around this by setting $x=t\pm(k+\frac12)\pi$, for small $t$. Then $\tan x\approx-\frac1t$, and $$-\frac1t=t\pm(k+\frac12)\pi\approx\pm(k+\frac12)\pi,$$ $$x\approx\pm(k+\frac12)\pi\mp\frac1{(k+\frac12)\pi}.$$

In the case of $\tan x=x^2$, the asymptotes are crossed even closer, but in an asymmetric way. The $t$ equation is of the third degree, but we can use $$-\frac1t=\Big(t+(\pm k+\frac12)\pi\Big)^2\approx\Big((\pm k+\frac12)\pi\Big)^2,$$ $$x\approx(\pm k+\frac12)\pi-\frac1{((\pm k+\frac12)\pi)^2}.$$

Answer 2

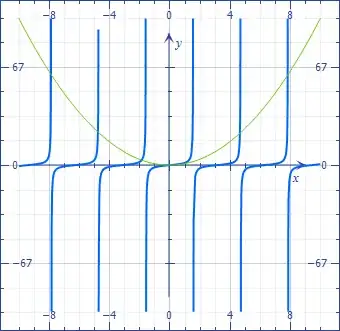
There is no analytical solution to equations which mix polynomials and trigonometric function. All the work has to be done using numerical methods.

One of the simplest root-finding method is Newton, which, starting from a "reasonable" guess $x_0$, will update it according to $$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$

For illustration purposes, let us take the case of $$f(x)=\tan(x) -5 x^2$$ for which we want to find some roots. A rough plot of the function reveals that it exists at least a root close to $1.5$; so this is our $x_0$.

Starting from this point, Newton procedure leads to the following iterates :$1.48457$, $1.48000$, $1.47971$ which is the solution for six significant figures.