How to get the correct angle of the ellipse after approximation

Question

I need to get the correct angle of rotation of the ellipses. These ellipses are examples. I have a canonical coefficients of the equation of the five points.

$$Ax ^ 2 + Bxy + Cy ^ 2 + Dx + Ey + F = 0$$

Ellipses:

Points:

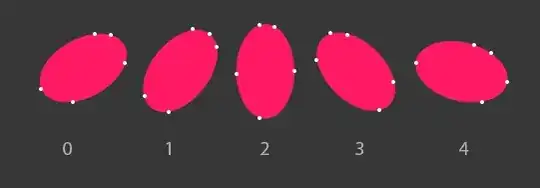
Zero ellipse:   [16,46]  [44,19]  [50,35]  [31,61]  [17,54]
First ellipse:  [14,95]  [47,71]  [55,83]  [23,107] [16,103]
Second ellipse: [12,128] [36,117] [58,128] [35,146] [13,136]
Third ellipse:  [16,164] [29,157] [54,188] [40,195] [17,172]
Fourth ellipse: [22,236] [31,207] [50,240] [40,252] [26,244]

Coefficients:

Zero ellipse                 First ellipse                Second ellipse                Third ellipse                  Fourth ellipse
A: 0.00039679682899033947    A: 0.00007365946131786486    A: 0.000021675708916102692    A: 0.00004189611868790682      A: 0.00004418821462144713
B: 0.00021821614636627075    B: 0.00006770936206052314    B: -0.000002834437159146921   B: -0.00004283926773569747     B: -0.000012890924982902275
C: 0.00024184103978866782    C: 0.00009244517004290531    C: 0.000057745675577137415    C: 0.00003944519997403195      C: 0.000020104667194164587
D: -0.03490717401354479      D: -0.01110309000831378      D: -0.0011544916677563865     D: 0.0046141642800698515       D: -0.00016090203479326006
E: -0.026421911476591453     E: -0.01877226426820658      E: -0.015086084806642279      E: -0.012396706675782408       E: -0.008774013189179199
F: 1.0                       F: 1.0                       F: 1.0                        F: 1.0                         F: 1.0

I successfully find the coordinates of the center and the length of the axes. But I get the wrong rotation.

I get the angle using the equation: $$\theta = \frac{1}{2} \arctan \left( \frac{B}{A-C} \right) $$

Angles result:

Zero ellipse:    0.4766612094205555
First ellipse:  -0.6500786401646479
Second ellipse:  0.03921024408607312
Third ellipse:  -0.7568233305427435
Fourth ellipse: -0.24572750447422026

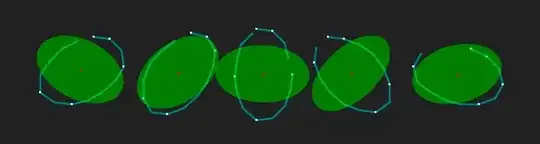
Visualization of the result:

How do I calculate the correct angle? And how to convert the value to degrees without errors?

UPDATED:

I wrote the algorithm here. The first set points angle is not correct. In the second set of points, the correct angle. You can put your own values and see the result.

UPDATED: SOLVED!

Based on the response of @Ng Chung Tak, I managed to get into the code and implement the right formula!

Implementation of the code here.

Formula:

$$\theta = \tan^{-1} \left( \frac{C-A}{B}+\frac{\sqrt{(A-C)^{2}+B^{2}}}{B} \: \right) $$

Result:

Thanks to all!

Answer 1

There're two principal axes in general, so

\begin{align*} \theta &=\frac{1}{2} \tan^{-1} \frac{B}{A-C}+\frac{n\pi}{2} \\ &= \tan^{-1} \left( \frac{C-A}{B} \color{red}{\pm} \frac{\sqrt{(A-C)^{2}+B^{2}}}{B} \: \right) \\ \end{align*}

The centre is given by $$(h,k)= \left( \frac{2CD-BE}{B^2-4AC}, \frac{2AE-BD}{B^2-4AC} \right)$$

Transforming to $$\frac{A+C \color{red}{\pm} \sqrt{(A-C)^{2}+B^{2}}}{2} x'^2+ \frac{A+C \color{red}{\mp} \sqrt{(A-C)^{2}+B^{2}}}{2} y'^2+ \frac {\det \begin{pmatrix} A & \frac{B}{2} & \frac{D}{2} \\ \frac{B}{2} & C & \frac{E}{2} \\ \frac{D}{2} & \frac{E}{2} & F \end{pmatrix}} {\det \begin{pmatrix} A & \frac{B}{2} \\ \frac{B}{2} & C \\ \end{pmatrix}}=0$$

where $\begin{pmatrix} x' \\ y' \end{pmatrix}= \begin{pmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{pmatrix} \begin{pmatrix} x-h \\ y-k \end{pmatrix}$.

The axes will match, up to reflection about the axes of symmetry, when the $\color{red}{\text{case}}$ (upper or lower) agrees.

Numerical example

Given five points: $(2,1)$, $(1,1)$, $(-2,-2)$, $(-1,-2)$, $(1,-1)$

$A=1$, $B=-2$, $C=2$, $D=-1$, $E=2$, $F=-2$

$$(h,k)=(0,-0.5)$$

$$\det \begin{pmatrix} A & \frac{B}{2} & \frac{D}{2} \\ \frac{B}{2} & C & \frac{E}{2} \\ \frac{D}{2} & \frac{E}{2} & F \end{pmatrix} = ACF-\frac{A E^2+C D^2+F B^2-EDB}{4}=-\frac{5}{2}$$

$$\det \begin{pmatrix} A & \frac{B}{2} \\ \frac{B}{2} & C \end{pmatrix} = -\frac{B^2}{4}+AC=1$$

$$\frac{A+C \pm \sqrt{(A-C)^{2}+B^{2}}}{2}=\frac{3 \pm \sqrt{5}}{2}$$

Using upper case convention:

$$\frac{3+\sqrt{5}}{2} x'^2+\frac{3-\sqrt{5}}{2} y'^2=\frac{5}{2}$$

$$\frac{x'^2}{a^2}+\frac{y'^2}{b^2}=1$$

$$(x',y')= (a\cos t,b\sin t)$$

where $\displaystyle \begin{pmatrix} a \\ b \end{pmatrix}= \begin{pmatrix} \sqrt{\frac{5}{3+\sqrt{5}}} \\ \sqrt{\frac{5}{3-\sqrt{5}}} \end{pmatrix}$

$$\theta = \tan^{-1} \left( \frac{C-A}{B}+\frac{\sqrt{(A-C)^{2}+B^{2}}}{B} \: \right) = \tan^{-1} \left( -\frac{\sqrt{5}+1}{2} \right) \approx -58.28^{\circ} $$

\begin{align*} \begin{pmatrix} x \\ y \end{pmatrix} &= \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix} \begin{pmatrix} x' \\ y' \end{pmatrix}+ \begin{pmatrix} h \\ k \end{pmatrix} \\ &&\\ &= \begin{pmatrix} h+x'\cos \theta-y'\sin \theta \\ k+x'\sin \theta+y'\cos \theta \end{pmatrix} \\ &&\\ &= \begin{pmatrix} \sqrt{\frac{5}{2}+\sqrt{5}\,} \, \sin t+ \sqrt{\frac{5}{2}-\sqrt{5}\,} \, \cos t \\ -\frac{1}{2}+ \frac{\sqrt{5+\sqrt{5}}}{2} \, \sin t- \frac{\sqrt{5-\sqrt{5}}}{2} \, \cos t \end{pmatrix} \end{align*}

Answer 2

Justification of the formula:

After centering (translation to let the linear terms vanish), the equation becomes $$Ax^2+Bxy+Cy^2+F'=0.$$

Then you apply a rotation of angle $\theta$ to let the mixed term $Bxy$ vanish from the quadratic terms,

$$A(x\cos\theta-y\sin\theta)^2+B(x\cos\theta-y\sin\theta)(x\sin\theta+y\cos\theta)+C(x\sin\theta+y\cos\theta)^2.$$

This is achieved when

$$2(C-A)\cos\theta\sin\theta+2B(\cos^2\theta-\sin^2\theta)=(C-A)\sin(2\theta)+2B\cos(2\theta)=0.$$

(Then you can rewrite $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$.)

Hence,

$$\tan(2\theta)=\frac{2B}{A-C}.$$

The angle $\theta$ is undeterminate by a multiple of a quater turn, as the ellipse has two symmetry axis.

Answer 3

Although it sounds like a question, for calculation did you use atan2 function or atan function? Quadrant placement is also important.