Given ellipse of axes $a$ and $b$, find axes of tangential and concentric ellipse at angle $t$

Question

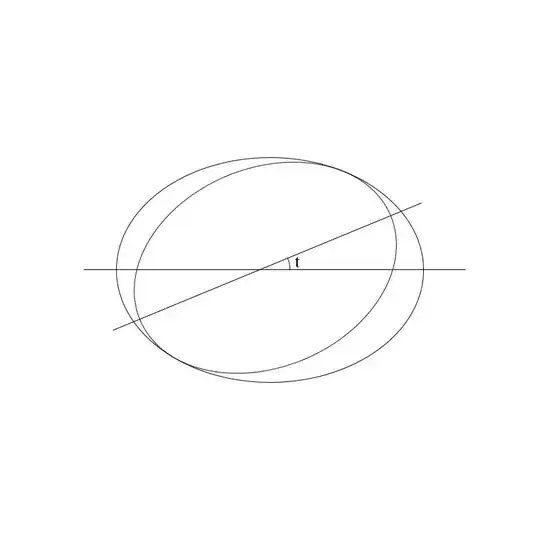
Let’s say I have an ellipse with horizontal axis $a$ and vertical axis $b$, centered at $(0,0)$. I want to compute $a’$ and $b’$ of a smaller ellipse centered at $(0,0)$, with the axes rotated by some angle $t$, tangent to the bigger ellipse and $\frac{a’}{b’}=\frac{a}{b}$.

Answer 1

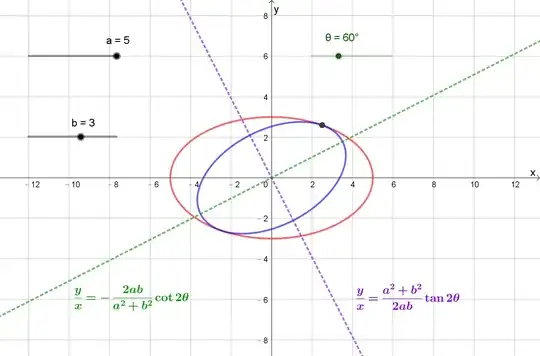
Let the oblique ellipse be

$$ \frac{x^2}{a^2}+ \frac{y^2}{b^2}-1=k \left( \frac{x\sin \theta}{a}- \frac{y\cos \theta}{b} \right)^2$$

which touches the standard ellipse at $(a\cos \theta,b\sin \theta)$.

This can be easily verified by plugging the point $(x',y')=(a\cos \theta,b\sin \theta)$ in the both ellipses and also have the same tangent line by referring to the useful fact in the very last of the post.

By finding the eigenvalues $(\lambda_1 <\lambda_2)$ of the matrix $\mathbb{M}$, namely

\begin{align} \mathbb{M} &= \begin{pmatrix} A & \frac{B}{2} \\ \frac{B}{2} & C \end{pmatrix} \\ &= \begin{pmatrix} \dfrac{1-k\sin^2 \theta}{a^2} & \dfrac{k\sin \theta \cos \theta}{ab} \\ \dfrac{k\sin \theta \cos \theta}{ab} & \dfrac{1-k\cos^2 \theta}{b^2} \end{pmatrix} \end{align}

Using Mathematica, we can get

$$\frac{\lambda_2}{\lambda_1}=\frac{a^2}{b^2} \implies k=\frac{(a^4-b^4)\cos 2\theta}{(a^2\cos^2 \theta+b^2\sin^2 \theta)^2}$$

which gives smaller ellipse if $k<0 \implies \cos 2\theta<0$ providing $a>b$.

Due to similarity, the new semi-axes are scaled by the same factor which can be determined by the determinant of the matrix $\mathbb{M}$.

Now,

\begin{align} \lambda_1 \lambda_2 &= \det \mathbb{M} \\ \frac{1}{a'^2 b'^2} &= AC-\frac{B^2}{4} \\ &= \frac{1-k}{a^2 b^2} \\ \frac{ab}{a'b'} &= \sqrt{1-k} \\ &= \frac{a^2\sin^2 \theta+b^2\cos^2 \theta} {a^2\cos^2 \theta+b^2\sin^2 \theta} \\ \frac{a'}{a} &= \frac{b'}{b} \\ &= \sqrt{ \frac{a^2\cos^2 \theta+b^2\sin^2 \theta} {a^2\sin^2 \theta+b^2\cos^2 \theta}} \end{align}

Using the result of another answer of mine, the angle of rotation is given by

\begin{align*} t &= \tan^{-1} \left( \frac{C-A}{B} \pm \frac{\sqrt{(A-C)^{2}+B^{2}}}{B} \: \right) \\ t_1 &= \tan^{-1} \left( -\frac{2ab}{a^2+b^2} \cot 2\theta \right) \tag{semi-axis $a$} \\ t_2 &= \tan^{-1} \left( \frac{a^2+b^2}{2ab} \tan 2\theta \right) \tag{semi-axis $b$} \end{align*}

In principle, $\theta$ can be solved in terms of $t$ explicitly. The work is tedious and verified experimentally by using Mathematica.

\begin{align} C & \equiv 2ab\cos t \\ S & \equiv (a^2+b^2)\sin t+\sqrt{(a^2+b^2)^2\sin^2 t+C^2} \\ \sqrt{1-k} &= \frac{a^2 S^2+b^2 C^2}{a^2 C^2+b^2 S^2} \end{align}

Finally by rotational transformation, the oblique ellipse can be expressed as

$$ \frac{(x\cos t+y\sin t)^2}{a^2}+ \frac{(y\cos t-x\sin t)^2}{b^2}= \frac{a^2 C^2+b^2 S^2}{a^2 S^2+b^2 C^2}$$

Further application

Illustration of spiral galaxy

Useful fact:

Equation of tangent for conics $ax^2+2hxy+by^2+2gx+2fy+c=0$ at the point $(x',y')$ is given by

$$ax'x+h(y'x+x'y)+by'y+g(x+x')+f(y+y')+c=0$$

Answer 2

Let the ratio $r= \frac{a’}a=\frac{b’}b$. Then, the inscribed ellipse with the tilt angle $t$ is

$$\frac{(x\cos t+y\sin t)^2}{r^2a^2}+ \frac{(-x\sin t+y\cos t)^2}{r^2b^2}=1\tag 1 $$

Also, the inscribed ellipse can be expressed as

$$ \frac{x^2}{a^2}+\frac{y^2}{b^2}-k\left( \frac{x\sin \theta}{a}-\frac{y\cos \theta}{b}\right)^2=1\tag 2$$

as pointed out by @Ng Chung Tak. Match the terms of $x^2$, $y^2$ and $xy$ between (1) and (2) to establish the system of equations below

\begin{align}k\sin 2\theta &=\frac{b^2-a^2}{r^2ab}\sin 2t\\ 1-k\sin^2 \theta &= \frac1{r^2b^2}(b^2\cos^2 t+a^2\sin^2t)\\ 1-k\cos^2 \theta &= \frac1{r^2a^2}(a^2\cos^2 t+b^2\sin^2t)\\ \end{align}

Plug the 1st equation into the others to eliminate $k$

$$r^2- \frac{b^2\cos^2 t+a^2\sin^2t}{b^2}= \frac{b^2-a^2}{2ab}\sin 2t\tan\theta $$

$$r^2- \frac{a^2\cos^2 t+b^2\sin^2t}{a^2}= \frac{b^2-a^2}{2ab}\sin 2t\cot\theta $$

Then, multiply the two equations to eliminate $\theta$. After simplification $$r^4 -( 2+\Delta^2)r^2+1=0$$

where $\Delta = \left( \frac a b - \frac b a\right)\sin t$. Solve to obtain the axis ratio

$$r= \sqrt{1+\frac{\Delta^2}4}-\frac{\Delta}2$$

Thus, the axes of the smaller ellipse are

$$a’ = ra, \>\>\>\>\>b’= rb$$

As expected, $r=1$ in the special case of $t=0$, and $r=\frac b a$ of $t=\frac\pi2$.

Answer 3

The original ellipse has the equation

$ r^T Q r = 1 $

where $r = [ x, y] ^ T $ and $Q$ is a symmetric positive definite $2 \times 2 $ matrix.

The scaled inner ellipse has the equation

$ r^T (\alpha^2 R Q R^T ) r = 1 $

for $\alpha \lt 1 $. Matrix $R$ is a known rotation matrix because $t$ is known.

Let the point of tangency between the two be $r_1$, then the gradients are proportional, i.e.

$ Q r_1 = K \alpha^2 R Q R^T r_1 $

Pre-multiplying by $r_1^T$, we find that $K = 1 $

Hence,

$ (Q - \alpha^2 R Q R^T ) r_1 = 0 $

Since $r_1$ is different than the zero vector, then $r_1$ is the eigenvector associated with the zero eigenvalue of $ (Q - \alpha^2 R Q R^T ) $. We don't care about $r_1$, we just need to find $\alpha$. Since the eigenvalue we want is $0$, then we want $\det( Q - \alpha^2 R Q R^T ) = 0 $

Now, let $A = \dfrac{1}{a^2}, B = \dfrac{1}{b^2} $, then

$Q = \begin{bmatrix} A && 0 \\ 0 && B \end{bmatrix}$

and

$ \alpha^2 R Q R^T = \alpha^2 \begin{bmatrix} A \cos^2 t + B \sin^2 t && (A - B) \cos t \sin t \\ (A - B) \cos t \sin t && A \sin^2 t+ B \cos^2 t \end{bmatrix} = \alpha^2 \begin{bmatrix} Q'_{11} && Q'_{12} \\ Q'_{12} && Q'_{22} \end{bmatrix}$

Therefore, we want to solve for $\alpha$ the following equation:

$ (A - \alpha^2 Q'_{11} ) (B - \alpha^2 Q'_{22} ) - \alpha^4 {Q'_{12}}^2 = 0 $

This simplifies to

$ \alpha^4 \det(Q') - \alpha^2 (A Q'_{22} + B Q'_{11}) + A B = 0 $

And since $\det(Q') = A B$ , this becomes simply

$ \alpha^4 A B - \alpha^2 (A Q'_{22} + B Q'_{11}) + A B = 0 $

Applying this analysis to the ellipse

$ \dfrac{x^2}{5^2} + \dfrac{y^2}{2^2} = 1$

with $ t = \dfrac{\pi}{6} $, we get the following ellipse (I took the value of $\alpha$ that is less than $1$, the other value gives the ellipse that is tangent to the given ellipse but circumscribes it.).