Intersection of two ellipses at exactly 2 points

Question

Thanks for your time. Let us consider the ellipses as $x^TAx=k$ and $x^TBx=l$. We can assume that we know $A$ and $B$. Suppose if we give one value to $k$, then we can adjust $l$ such that one ellipse will lie entirely inside the other ellipse and touch exactly at two points. I was wondering if there is any analytical way to obtain the solutions $(x,k,l)$ for this system. If not, how to numerically solve this? Any help much appreciated!

Answer 1

We can assume WLOG (up to division by a constant) that the first ellipse $(E)$ has equation

$$X^TAX=1$$

Let $X^TBX=\ell$ be the second variable ellipse that we will call $(E_{\ell})$.

Result : the values of $\ell$ warranting an internal, resp external, tangency of $(E_{\ell})$ with $(E)$ are the smallest, resp. largest, of the eigenvalues of matrix :

$$C:=A^{-1}B$$

Moreover, the points of contact of the curves are given by eigenvectors of this matrix $C$.

Proof :

Curve $(E_{\ell})$ touches curve $(E)$ in a point $X=\pmatrix{x\\y}$ if the two curves have proportional gradients (normal vectors) in this point :

$$2BX = \lambda 2AX\tag{1}$$

for a certain $\lambda$. Pre-multiplying (1) by $A^{-1}$ :

$$\underbrace{(A^{-1}B)}_CX=\lambda X\tag{2}$$

in which we recognize an eigenvector and an eigenvalue of $C$.

Now, with if we multiply LHS and RHS of (1) by $X^T$, we get :

$$X^TBX = \lambda \underbrace{X^TAX}_{=1}\tag{3}$$

That's all...

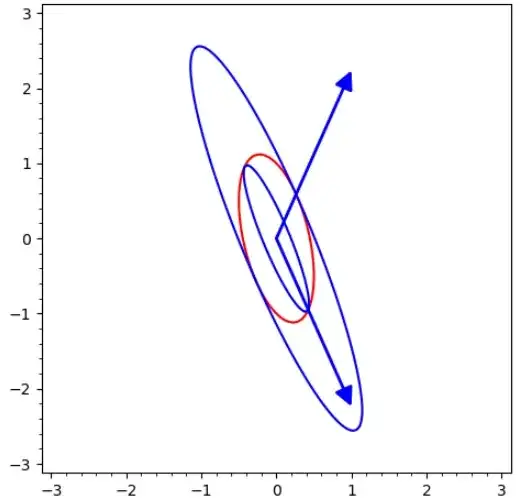
Fig. 1 : Ellipse $(E)$ is figured in red. The two ellipses $(E_{\ell})$ internaly and externaly tangent to $(E)$ are in blue.

The Sage program that has produced the figure above is given below ; you can easily execute it by calling https://sagecell.sagemath.org/, copy-paste the program into the edit window, then press button "Evaluate".

Please note

• that $X^TAX$ is represented as the dot product of $X$ by $AX$.

• that the (unnormalized) eigenvectors indicate the direction of tangency points. One can normalize them in order that their extremities are precisely on these points.

  var('x y');
  A=matrix([[5,1],[1,1]])
  B=matrix([[5,2],[2,1]])
  C=A.inverse()*B
  D=C.eigenmatrix_right()
  Diag=D[0];# matrix with eigenvalues on diagonal
  VP=D[1];
  X=vector([x,y])
  L=3
  g=implicit_plot(X.dot_product(A*X)-1,(x,-L,L),(y,-L,L),color='red')
  for k in range(2) :
     La=Diag[k][k];# k-th eigenvalue (k=0,1)
     g+=implicit_plot(X.dot_product(B*X)-La,(x,-L,L),(y,-L,L))
     g+=plot(VP.column(k));
  show(g)
  

Answer 2

Assume that $A, B, k$ are given where $A, B$ are symmetric positive definite $2 \times 2 $ matrices, and $k \gt 0$. The solution of

$ x^T A x = k $

is the ellipse

$ x = v_1 \cos t + v_2 \sin t $

where $v_1, v_2$ are $2 \times 1$ vectors.

This is the parametric equation of the ellipse.

Substitute this into $x^T B x = l $ , then

$ (v_1 \cos t + v_2 \sin t )^T B (v_1 \cos t + v_2 \sin t ) = l $

which expands into

$ \cos^2 t (v_1^T B v_1) + \sin^2 t (v_2^T B v_2) + 2 \cos t \sin t (v_1^T B v_2) = l $

Further, this can be written as

$ \cos(2 t) ( v_1^T B v_1 - v_2^T B v_2) + \sin(2 t ) (2 v_1^T B v_2) = 2l - v_1^T B v_1 - v_2^T B v_2 $

Since we want only two solutions for $t$. And obviously these two solutions are separated by $ \pi $, then $2 t_2 = 2 t_1 + 2 \pi $. Therefore there is only one solution for $(2 t)$. This can only happen if

$ (v_1^T B v_1 - v_2^T B v_2 )^2 + (2 v_1^T B v_2 )^2 = ( 2 l - v_1^T B v_1 - v_2 ^T B v_2 )^2 $

And this gives two values of $l$

$ l = \dfrac{1}{2} \bigg( v_1^T B v_1 + v_2 B v_2 \pm \sqrt{(v_1^T B v_1 - v_2^T B v_2 )^2 + (2 v_1^T B v_2 )^2} \bigg)$

The smaller value corresponds to the case when the second ellipse is completely inside the first ellipse, and the larger value to the case when the second ellipse is completely outside the first ellipse.

I've written a small program to plot the two ellipses for each value of $l$. The plots show that the formula for $l$ is correct.

The code is shown below.

Public Sub tangential_ellipses()
Dim d1(2, 2), d2(2, 2) As Double
Dim d1isq(2, 2), d2isq(2, 2) As Double
Dim a(2, 2), b(2, 2) As Double
Dim r1(2, 2), r1t(2, 2), r2(2, 2), r2t(2, 2) As Double
Dim v1(2, 2), v2(2, 2), v3(2, 2), v4(2, 2) As Double
th1 = 10 * p / 180
th2 = 130 * p / 180
d1(1, 1) = 1 / 7 ^ 2
d1(2, 2) = 1 / 4 ^ 2
d1isq(1, 1) = 7
d1isq(2, 2) = 4
d2(1, 1) = 1 / 5 ^ 2
d2(2, 2) = 1 / 3.5 ^ 2
d2isq(1, 1) = 5
d2isq(2, 2) = 3.5
r1(1, 1) = Cos(th1)
r1(2, 1) = Sin(th1)
r1(1, 2) = -Sin(th1)
r1(2, 2) = Cos(th1)
r2(1, 1) = Cos(th2)
r2(2, 1) = Sin(th2)
r2(1, 2) = -Sin(th2)
r2(2, 2) = Cos(th2)
Call transpose(2, 2, r1, r1t)
Call transpose(2, 2, r2, r2t)
Call multiply(2, 2, 2, r1, d1, a)
Call multiply(2, 2, 2, a, r1t, a)
Call multiply(2, 2, 2, r2, d2, b)
Call multiply(2, 2, 2, b, r2t, b)
k = 1
' x^T a x = k
' x = V u
' where V = R D1^(-1/2)
Call multiply(2, 2, 2, r1, d1isq, v1)
For i = 1 To 2
u1(i) = v1(i, 1)
u2(i) = v1(i, 2)
Next i
c1 = xtqy(2, b, u1, u1)  ' u1^T b u1
c2 = xtqy(2, b, u2, u2)  ' u2^T b u2
c3 = xtqy(2, b, u1, u2)  ' u1^T b u2
l1 = 0.5 * (c1 + c2 - Sqr((c1 - c2) ^ 2 + (2 * c3) ^ 2))
l2 = 0.5 * (c1 + c2 + Sqr((c1 - c2) ^ 2 + (2 * c3) ^ 2))
Call multiply(2, 2, 2, r2, d2isq, v2)
Call mscale(2, 2, v2, Sqr(l1), v3)
Call mscale(2, 2, v2, Sqr(l2), v4)
k = 1
narcs = 0
ipass = 2
u3(1) = 0
u3(2) = 0
Call draw_ellipse(u3, v1, 5)
Call draw_ellipse(u3, v3, 46)
Call draw_ellipse(u3, v4, 46)
Call plot_curve(0, 1, 0, 0, 0, "", "")
End Sub

---

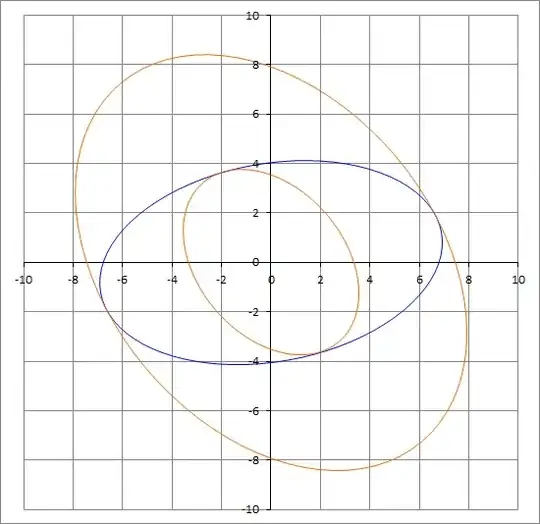
The output of this code is the original ellipse (blue) and the two tangential ellipses (orange).

---

Appendix: How to compute $v_1$ and $v_2$

From the given equation

$ x^T A x = k $

Divide through by $k$, you get the equation in standard format

$ x^T \left( \dfrac{A}{k} \right) x = 1 $

Let $G= \dfrac{A}{k} $, then you have

$ x^T G x = 1 $

Diagonlize $G$, that is, write it as

$G = R D R^T $

where $R = \begin{bmatrix} \cos \theta && - \sin \theta \\ \sin \theta && \cos \theta \end{bmatrix} $

The angle $\theta$ is given by

$ \theta = \dfrac{1}{2} \tan^{-1} \left( \dfrac{ 2 G_{12} } {G_{11} -G_{22} } \right) $

And the two diagonal elements of $D$ are given by

$ D_{11} = A_{11} \cos^2 \theta + A_{22} \sin^2 \theta + 2 A_{12} \sin \theta \cos \theta $

$ D_{22} = A_{11} \sin^2 \theta + A_{22} \cos^2 \theta - 2 A_{12} \sin \theta \cos \theta $

Now you have

$ x^T R D R^T x = 1 $

Define $z = R^T x $ , then

$ z^T D z = 1 $

i.e. $D_{11} z_1^2 + D_{22} z_2^2 = 1 $

Let $a = \dfrac{1}{\sqrt{D_{11}}} $ and $ b = \dfrac{1}{\sqrt{D_{22}}} $

Then

$ \dfrac{z_1^2}{a^2} + \dfrac{z_2^2}{b^2 } = 1$

whose parametric solution is

$ (z_1, z_2) = ( a \cos t , b \sin t ) $

But $z = R^T x $, i.e. $x = R z $

Hence

$ x = R \begin{bmatrix} a \cos t \\ b \sin t \end{bmatrix} = R \begin{bmatrix} a && 0 \\ 0 && b \end{bmatrix} \begin{bmatrix} \cos t \\ \sin t \end{bmatrix} $

Let the matrix $V$ be define by

$ V = [v_1, v_2] = R \begin{bmatrix} a && 0 \\ 0 && b \end{bmatrix} $

that is, $v_1$ is the first column of the matrix defined on the right hand side and $v_2$ is the second column. Then it follows that

$ x = V \begin{bmatrix} \cos t \\ \sin t \end{bmatrix} = v_1 \cos t + v_2 \sin t $

$v_1$ and $v_2$ point in the direction of the semi-major and semi-minor axes (not necessarily in this particular order) and their lengths are the lengths of the semi-axes.

Answer 3

We can solve explicitly this problem with the use of tangency.

Given two ellipses

$$ \cases{ a_1 x^2+b_1 x y + c_1 y^2 - k = 0\\ a_2 x^2+b_2 x y + c_2 y^2 - l = 0 } $$

eliminating $y$ we have

$$ p(x) = \mu_1 k^2+ \mu_2 l k + \mu_3 l^2 + \mu_4 k x^2 + \mu_5 l x^2 + \mu_6 x^4=0 $$

and as the two ellipses are tangent at two different points, necessarily we have

$$ p(x) = \mu_6(x-x_1)^2(x-x_2)^2 $$

where $x_2, x_2$ are the tangency coordinates, and this should be true for all $x$ then

$$ \cases{ \mu_1 k^2 + \mu_2 k l + \mu_3 l^2 - \mu_6 x_1^2 x_2^2=0\\ \mu_4 k + \mu_5 l - \mu_6 x_1^2 - 4 \mu_6 x_1 x_2 - \mu_6 x_2^2=0\\ x_1 + x_2 = 0 } $$

Three equations and four unknowns $(x_1,x_2,l,k)$ so we can determine: $(x_1(k),x_2(k),l(k))$ or $(x_1(l),x_2(l),k(l))$.

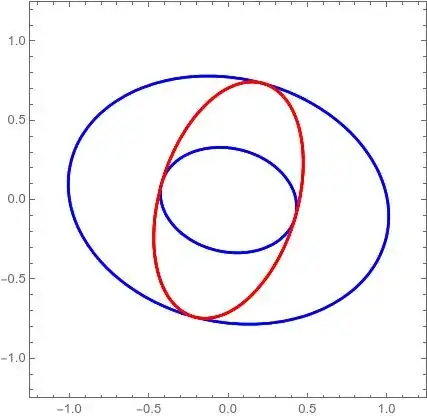
Making $a_1=3,a:2=5,b_1=1,b_2=-2,c_1=5,c_2 = 2$ we have $\mu_1=4,\mu_2=-20,\mu_3=25,\mu_4=52,\mu_5=-202,\mu_6=493$ and choosing $l=1$ we obtain for $k$

$$ \left\{\frac{1}{18} (32 - \sqrt{493}), \frac{1}{18} (32 + \sqrt{493})\right\} $$

Attached the plot showing the result