0

Question. Can a conic section curve have two distinct pairs of focus and directrix?

Attempt. I cannot think of a rigorous and logical way to convince myself of the uniqueness. But for me it is like two degrees of freedom (focus and directrix) define a single degree of freedom (a curve based on the constant eccentricity); intuitively for me, it might not be unique?

Comment. I do not need the answer to be rigorous; just some framework or hint would satisfy. Thank you!

IncredibleSimon
  • 933
  • Yes for a hyperbola. – user10354138 Feb 12 '21 at 00:58
  • Draw an example for each kind of conic section and think about whether the focus and directrix could have been somewhere other than where you drew them. – Steve Kass Feb 12 '21 at 00:58
  • I tried to take a parabola, in specific $y^2=4ax$ where $a$ is a positive real, as an example; I tried to scale $a$ by some positive multiple like $2$, which would make the focus and directrix equally further away from the origin, and the equation relating $y$ and $x$ changed. Hmm, by eyeballing, parabola could have another pair of focus and directrix, but based on the equation of curve it does not seem so... @SteveKass – IncredibleSimon Feb 12 '21 at 01:11
  • I'm intrigued. Let me think about it for a while. @user10354138 – IncredibleSimon Feb 12 '21 at 01:12
  • Ellipses and hyperbolas have two foci, each having its own directrix. That's obvious by symmetry. – Intelligenti pauca Feb 12 '21 at 10:37
  • Doing this just for a parabola wasn't enough. ;) For a circle, there are lots of possibilities for a directrix, and for an ellipse, there are two possibilities for the focus/directrix pair. – Steve Kass Feb 12 '21 at 19:12

2 Answers2

1

We can always find the unique pair of Dandelin spheres from the conic section without ambiguity.

$\hspace{5cm}$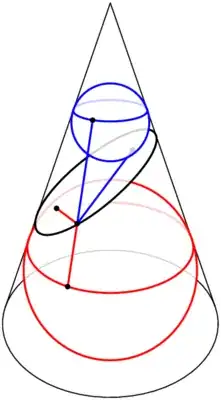enter image description here

Each Dandelin sphere touches both the right circular cone and the conic section on the corresponding focus.

See also detail discussion with animation in the link here and another post of mine about focal conics and confocal quadrics here.

For a general conic, namely

$$0= \begin{pmatrix} x & y & 1 \\ \end{pmatrix} \begin{pmatrix} a & h & g \\ h & b & f \\ g & f & c \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$$

Its foci $z=x+yi$ are given by the complex quadratic, namely

$$Cz^2-2(G+Fi)z+(A-B)+2Hi=0$$

where capital letters $A,B, \ldots$ represent co-factors of the corresponding entries of small letters $a,b, \ldots$ of the matrix respectively. That is

$$ \begin{pmatrix} A & H & G \\ H & B & F \\ G & F & C \end{pmatrix} = \begin{pmatrix} bc-f^2 & fg-ch & fh-bg \\ fg-ch & ac-g^2 & gh-af \\ fh-bg & gh-af & ab-h^2 \end{pmatrix}$$

See another post for finding the principal axes, etc.

Ng Chung Tak
  • 18,990
0

Commenters have pointed out that ellipses and hyperbolae have two focus/directrix pairs. But I assume that's not what the OP is after.

As another answer points out, given a conic you can uniquely determine its foci, center, axes, directrices, etc.

But OP would like to reconcile this with "two degrees of freedom (focus and directrix) define a single degree of freedom (a curve based on the constant eccentricity)"

For a given conic and its focus, the directrix is the polar of the focus with respect to the conic. So the focus/directrix pair are really a single degree of freedom in this context.

brainjam
  • 8,626